Табличный метод генерации нормально распределенных чисел

Для этого нормальное число можно взять из справочника в таблице функции Лапласа и получить случайное число по методу взятия обратной функции (см. лекцию 24): x = F ^–1(r), где F — интегральная функция Лапласа.

Технически это означает, что надо разыграть случайное равномерно распределенное число r из интервала [0; 1] стандартным ГСЧ (см. таблицу абсолютно случайных проверенных чисел), найти равное ему число в таблице значений функции Лапласа в столбце F и по строке определить случайную величину x, соответствующую этому числу.

Недостатком метода является необходимость хранения в памяти компьютера всей таблицы чисел функции Лапласа.

Метод генерации нормально распределенных чисел, использующий центральную предельную теорему

Общая идея метода следующая: требуется сложить случайные числа с любым законом распределения, нормализовать их и перевести в нужный диапазон нормального распределения.

Допустим, что нам надо в целях имитации получить ряд случайных чисел x, распределенных по нормальному закону с заданными математическим ожиданием m_x и среднеквадратичным отклонением σ_x.

1. Сложим n случайных чисел, используя стандартный ГСЧ:

Согласно ЦПТ числа V образуют ряд значений, распределенный по нормальному закону. Эти числа тем лучше описывают нормальный закон, чем больше параметр n. На практике n берут равными 6 или 12. Заметим, что закон распределения чисел V имеет математическое ожидание m_V = n /2, σ_V = sqrt(n /12). Поэтому он является смещенным относительно заданного произвольного.

2. С помощью формулы z = (V – m_V)/ σ_V нормализуем этот ряд. Получим нормализованный закон нормального распределения чисел Z. То есть m_z = 0, σ_z = 1.

3. Формулой (сдвиг на m_x и масштабирование на σ_x) преобразуем ряд Z в ряд x: x = z · σ_x + m_x.

Пример. Смоделировать поток заготовок для обработки их на станке. Известно, что длина заготовки колеблется случайным образом. Средняя длина заготовки составляет 35 см, а среднеквадратичное отклонение реальной длины от средней составляет 10 см. То есть по условиям задачи m_x = 35, σ_x = 10. Тогда значение случайной величины будет рассчитываться по формуле: V = r ₁ + r ₂ + r ₃ + r ₄ + r ₅ + r ₆, где r — случайные числа из ГСЧ_рр [0; 1], n = 6.
X = σ_x · (sqrt(12/ n) · (V – n /2)) + m_x = 10 · sqrt(2) · (V – 3) + 35
или
X = 10 · sqrt(2) · ((r ₁ + r ₂ + r ₃ + r ₄ + r ₅ + r ₆) – 3) + 35.

Метод Мюллера

Совсем простым методом получения нормальных чисел является метод Мюллера, использующий формулы: Z = √(–2 · Ln(r ₁)) · cos(2 π · r ₂), где r ₁ и r ₂ — случайные числа из ГСЧ_рр [0; 1].

Можно также воспользоваться аналогичной формулой Z = √(–2 · Ln(r ₁)) · sin(2 π · r ₂), где r ₁ и r ₂— случайные числа из ГСЧ_рр [0; 1].

Пример. Материал поступает в цех один раз в сутки по 10 штук сразу. Расход материала из цеха случайный по нормальному закону с математическим ожиданием m = 10 и среднеквадратичным отклонением σ = 3.5. Вычислить вероятность дефицита на складе при запасе материала в начальный момент времени 20 штук.

При реализации в среде моделирования Stratum решение задачи будет выглядеть следующим образом.

z:= sqrt(–2 · ln(rnd)) · cos(2 · PI · rnd) x:= σ · z + m запас:= запас + 10 запас:= (запас – x) · ed(запас – x) дефицит:= дефицит + not(ed(запас – x)) N:= N + 1 P:= дефицит/N stop(N > k)

z — нормальное нормализованное случайное число; x — нормальное число, ежедневный расход материалов; запас — состояние склада: начало дня, моделирование прихода; запас — состояние склада: конец дня, моделирование расхода; дефицит — счетчик дней, в течение которых наблюдался дефицит; N — количество дней; P — вероятность дефицита; k — моделирование в течение k дней.

Моделирование системы
случайных величин

Часто на практике встречаются системы случайных величин, то есть такие две (и более) различные случайные величины X, Y (и другие), которые зависят друг от друга. Например, если произошло событие X и приняло какое-то случайное значение, то событие Y происходит хотя и случайно, но с учетом того, что X уже приняло какое-то значение.

Например, если в качестве X выпало большое число, то Y должно выпасть тоже достаточно большое число (если корреляция положительна). Весьма вероятно, что если человек имеет большой вес, то он, скорее всего, будет и большого роста. Хотя это НЕ ОБЯЗАТЕЛЬНО, это НЕ ЗАКОНОМЕРНОСТЬ, а корреляция случайных величин. Так как бывают, хотя и редко, люди с большим весом, но небольшого роста или с маленьким весом и высокие. И все таки основная масса тучных людей — высоки, а низких людей — имеют малый вес.

По определению, если случайные величины независимы, то f (x) = f (x ₁) · f (x ₂) · … · f (x_n).

xi — случайная независимая величина; f (xi) — плотность вероятности выпадения случайной независимой величины xi; f (x) — плотность вероятности выпадения вектора xслучайных независимых величин x 1, x 2, …, xn.

Если случайные величины зависимы, то f (x) = f (x ₁) · f (x ₂ | x ₁) · f (x ₃ | x ₂, x ₁) · … · f (x_n | x_{n – 1}, x_{n – 2}, …, x ₂, x ₁).

xj | xj – 1, …, x 1 — случайные зависимые величины: выпадение xj при условии, что выпали xj – 1, …, x 1; f (xj | xj – 1, …, x 1) — плотность условной вероятности появления xj, если выпали xj – 1, …, x 1; f (x) — вероятность выпадения вектора x случайных зависимых величин.

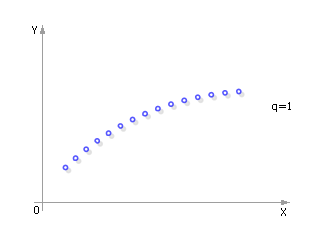
Пусть, к примеру, имеется два зависимых события — X и Y, распределенных по нормальному закону. X имеет математическое ожидание m_x и среднеквадратическое отклонение σ_x. Y имеет математическое ожидание m_y и среднеквадратическое отклонение σ_y. Коэффициент корреляции — q — показывает, насколько тесно связаны события X и Y. Если коэффициент корреляции равен единице, то зависимость событий X и Y взаимно однозначная: одному значению X соответствует одно значение Y (см. рис. 26.1).

Рис. 26.1. Вид зависимости двух случайных величин при положительном коэффициенте корреляции (q=1)

При q близких к единице возникает картина, показанная на рис. 26.2, то есть одному значению X могут соответствовать уже несколько значений Y (точнее, одно из нескольких значений Y, определяемое случайным образом); в этом случае события X и Y менее коррелированы, менее зависимы друг от друга.

Рис. 26.2. Вид зависимости двух случайных величин при положительном коэффициенте корреляции (0 < q < 1)

И, наконец, когда коэффициент корреляции стремится к нулю, возникает ситуация, при которой любому значению X может соответствовать любое значение Y, то есть события X и Y не зависят или почти не зависят друг от друга, не коррелируют друг с другом (см. рис. 26.3).

Рис. 26.3. Вид зависимости двух случайных величин при коэффициенте корреляции близком к нулю (q –> 0)

На всех графиках корреляция была принята положительной величиной. Если q < 0, то графики будут выглядеть так, как показано на рис. 26.4.

Рис. 26.4. Вид зависимости двух случайных величин при отрицательном коэффициенте корреляции a) q = –1; б) –1 < q < 0; в) q –> 0

На самом деле случайные события (X и Y) не могут принимать с равной вероятностью любые значения, как это имеет место на рис. 26.2. К примеру, в группе студентов не может быть людей сверхмалого или сверхбольшого роста; в основном, люди обладают неким средним ростом и разбросом вокруг этого среднего роста. Поэтому на одних участках оси X количество событий расположено гуще, на других — реже. (Плотность случайных событий, количество точек на графиках больше вблизи величин m_x). То же самое верно и для Y. И тогда рис. 26.2 можно изобразить более точно, так, как показано на рис. 26.5.

Рис. 26.5. Иллюстрация системы случайных зависимых величин

Для примера возьмем нормальное распределение, как самое распространенное. Математическое ожидание указывает на самые вероятные события, здесь число событий больше и график событий гуще. Положительная корреляция указывает (см. рис. 26.2), что большие случайные величины X вызывают к генерации большие Y. Отрицательная корреляция указывает (см. рис. 26.4), что большие случайные величины X стимулируют к генерации меньшие случайные величины Y. Нулевая и близкая к нулю корреляция показывает (см. рис. 26.3), что величина случайной величины X никак не связана с определенным значением случайной величины Y. Легко понять сказанное, если представить себе сначала распределения f (X) и f (Y) отдельно, а потом связать их в систему (см. рис. 26.6, рис. 26.7 и рис. 26.8).

Рис. 26.6. Генерация системы случайных величин при положительном коэффициенте корреляции

 

Рис. 26.7. Генерация системы случайных величин при отрицательном коэффициенте корреляции

 

Рис. 26.8.

Пример реализации алгоритма моделирования двух зависимых случайных событий X и Y. Условие: допустим, что X и Y распределены по нормальному закону с соответствующими значениями m_x, σ_x и m_y, σ_y. Задан коэффициент корреляции двух случайных событий q, то есть случайные величины X и Y зависимы друг от друга, Y не совсем случайно.

Тогда возможный алгоритм реализации модели будет следующим.

1. Разыгрывается шесть случайных равномерно распределенных на интервале [0; 1] чисел b ₁, b ₂, b ₃, b ₄, b ₅, b ₆; находится их сумма S: S = b ₁ + b ₂ + b ₃ + b ₄ + b ₅ + b ₆. Находится нормально распределенное случайное число x по следующей формуле: x = sqrt(2) · σ_x · (S – 3) + m_x, см.лекцию 25.

2. По формуле m_{y / x} = m_y + q · σ_y / σ_x · (x – m_x) находится математическое ожидание m_{y / x} (знак y / x означает, что y будет принимать случайные значения с учетом условия, что x уже принял какие-то определенные значения).

3. По формуле σ_{y / x} = σ_y · sqrt(1 – q ²) находится среднеквадратическое отклонение σ_{y / x} (знак y / x означает, что y будет принимать случайные значения с учетом условия, что x уже принял какие-то определенные значения).

4. Разыгрывается шесть случайных равномерно распределенных на интервале [0; 1] чисел r ₁, r ₂, r ₃, r ₄, r ₅, r ₆; находится их сумма k: k = r ₁ + r ₂ + r ₃ + r ₄ + r ₅ + r ₆. Находится нормально распределенное случайное число y по следующей формуле: y = sqrt(2) · σ_{y / x} · (k – 3) + m_{y / x} .

Распределение Пуассона

Наиболее общим случаем различного рода вероятностных распределений является биномиальное распределение. Воспользуемся его универсальностью для определения наиболее часто встречающихся на практике частных видов распределений.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: