Марковские случайные процессы с непрерывным временем

Итак, снова модель марковского процесса представим в виде графа, в котором состояния (вершины) связаны между собой связями (переходами из i -го состояния в j -е состояние), см. рис. 33.10.

Рис. 33.10. Пример графа марковского процесса с непрерывным временем

Теперь каждый переход характеризуется плотностью вероятности перехода λ_ij. По определению:

При этом плотность понимают как распределение вероятности во времени.

Переход из i -го состояния в j -е происходит в случайные моменты времени, которые определяются интенсивностью перехода λ_ij.

К интенсивности переходов (здесь это понятие совпадает по смыслу с распределением плотности вероятности по времени t) переходят, когда процесс непрерывный, то есть, распределен во времени.

С интенсивностью потока (а переходы — это поток событий) мы уже научились работать влекции 28. Зная интенсивность λ_ij появления событий, порождаемых потоком, можно сымитировать случайный интервал между двумя событиями в этом потоке.

где τ_ij — интервал времени между нахождением системы в i -ом и j -ом состоянии.

Далее, очевидно, система из любого i -го состояния может перейти в одно из нескольких состояний j, j + 1, j + 2, …, связанных с ним переходами λ_ij, λ_{ij + 1}, λ_{ij + 2}, ….

В j -е состояние она перейдет через τ_ij; в (j + 1)-е состояние она перейдет через τ_{ij + 1}; в (j + 2)-е состояние она перейдет через τ_{ij + 2} и т. д.

Ясно, что система может перейти из i -го состояния только в одно из этих состояний, причем в то, переход в которое наступит раньше.

Поэтому из последовательности времен: τ_ij, τ_{ij + 1}, τ_{ij + 2} и т. д. надо выбрать минимальное и определить индекс j, указывающий, в какое именно состояние произойдет переход.

Пример. Моделирование работы станка. Промоделируем работу станка (см. рис. 33.10), который может находиться в следующих состояниях: S ₀ — станок исправен, свободен (простой); S ₁ — станок исправен, занят (обработка); S ₂ — станок исправен, замена инструмента (переналадка) λ ₀₂ < λ ₂₁; S ₃ — станок неисправен, идет ремонт λ ₁₃ < λ ₃₀.

Зададим значения параметров λ, используя экспериментальные данные, получаемые в производственных условиях: λ ₀₁ — поток на обработку (без переналадки); λ ₁₀ — поток обслуживания; λ ₁₃ — поток отказов оборудования; λ ₃₀ — поток восстановлений.

Реализация будет иметь следующий вид (см. рис. 33.11).

Рис. 33.11. Пример моделирования непрерывного марковского процесса с визуализацией на временной диаграмме (желтым цветом указаны запрещенные, синим — реализовавшиеся состояния)

В частности, из рис. 33.11 видно, что реализовавшаяся цепь выглядит так: S ₀— S ₁— S ₀—…Переходы произошли в следующие моменты времени: T ₀— T ₁— T ₂— T ₃—…, где T ₀ = 0, T ₁ = τ₀₁, T ₂ = τ₀₁ + τ₁₀.

Задача. Поскольку модель строят для того, чтобы на ней можно было решить задачу, ответ которой до этого был для нас совсем не очевиден (см. лекцию 01), то сформулируем такую задачу к данному примеру. Определить долю времени в течение суток, которую занимает простой станка (посчитать по рисунку) T _ср = (T + T + T + T)/ N.

Алгоритм имитации будет иметь следующий вид (см. рис. 33.12).

Рис. 33.12. Блок-схема алгоритма моделирования непрерывного марковского процесса на примере имитации работы станка

Очень часто аппарат марковских процессов используется при моделировании компьютерных игр, действий компьютерных героев.

Фиксация и обработка статистических
результатов

В лекции 21 мы подробно познакомились со схемой статистического компьютерного эксперимента. В лекциях 21—26 мы рассмотрели практическую реализацию всех основных блоков (см. рис. 21.3) этой схемы. Сейчас важно научиться организовывать работу последних двух блоков — блок вычисления статистических характеристик (БВСХ) и блок оценки достоверности статистических результатов (БОД).

Итак, рассмотрим, как следует фиксировать статистические величины в результате эксперимента, чтобы получить надежную информацию о свойствах моделируемого объекта. Напомним, что обобщенными характеристиками случайного процесса или явления являются средние величины.

Вычисление средних

Вычисление средних величин во время эксперимента, который многократно повторяется, а результат его усредняется, может быть организовано несколькими способами:

• вся статистика вычисляется в конце;
• вся статистика вычисляется в процессе вычисления (по рекурсивным соотношениям);
• вся статистика вычисляется в классовых интервалах (этот метод совмещает универсальность первого метода и экономичность второго).

Способ 1. Вычисление всей статистики в конце. Для этого в процессе эксперимента значения X_i выходной (изучаемой) случайной величины X накапливается в массиве данных. После окончания эксперимента подсчитывается математическое ожидание (среднее) X и дисперсия D (характерный разброс величин относительно этого математического ожидания).

Часто используют среднеквадратичное отклонение σ = sqrt(D).

Заметим, что недостатком метода является неэффективное использование памяти, так как приходится накапливать и сохранять большое количество значений выходной величины в течение всего эксперимента, который может быть весьма продолжительным.

Второй минус заключается в том, что приходится дважды считывать массив X_i, так как воспользоваться формулой (2) в том виде, как она здесь записана, мы можем, только просчитав формулу (1) (от 1 до n), а потом еще раз прогнав для формулы (2) массив X_i.

Положительным моментом является сохранение всего массива данных, что дает возможность более подробного его изучения в дальнейшем при необходимости расследования тех или иных эффектов и результатов.

Способ 2. Вычисление всей статистики в процессе вычисления (по рекурсивным соотношениям). Этот способ предусматривает возможность хранить только текущее значение математического ожидания X_i и дисперсии D_i, подправляемое на каждой итерации. Это избавляет нас от необходимости постоянного хранения всего массива экспериментальных данных. Каждое новое данное X_i учитывается в сумме с весовым коэффициентом — чем более слагаемых i накоплено в сумме X_i, тем более ее значение важно по отношению к очередной поправке X_i, поэтому соотношение весовых коэффициентов i /(i + 1): 1/(i + 1).

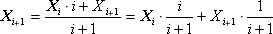
где X_i — очередное значение экспериментальной выходной величины.

Способ 3. Вычисление всей статистики в классовых интервалах. Этот способ предполагает, что в массив будут накапливать не все значения X_i, а только по значимым интервалам, в которых распределена случайная выходная величина X_i. Общий интервал изменения X_i разбивается на m подинтервалов, в каждом из которых фиксируется количество n_i, которое показывает, сколько раз X_i приняло значение из i -го интервала. При небольшом количестве интервалов (m ≈ 1) мы получаем способ 1, при количестве интервалов m = n мы получаем способ 2. В случае 1 < m < n получаем среднее решение — компромисс между занимаемой памятью и информативностью массива выходных данных.

⇐ Предыдущая19202122232425262728Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: