Биномиальное распределение

Пусть имеется некое событие A. Вероятность появления события A равна p, вероятность непоявления события A равна 1 – p, иногда ее обозначают как q. Пусть n — число испытаний, m — частота появления события A в этих n испытаниях.

Известно, что суммарная вероятность всех возможных комбинаций исходов равна единице, то есть:

1 = pⁿ + n · p^{n – 1} · (1 – p) + C_n^{n – 2} · p^{n – 2} · (1 – p)² + … + C_n^m · p^m · (1 – p) ^{n – m} + … + (1 – p) ⁿ.

pn — вероятность того, что в n испытаниях событие A произойдет n раз; n · pn – 1 · (1 – p) — вероятность того, что в n испытаниях событие A произойдет(n – 1) раз и не произойдет 1 раз; Cnn – 2 · pn – 2 · (1 – p)2 — вероятность того, что в n испытаниях событие Aпроизойдет (n – 2) раза и не произойдет 2 раза; Pm = Cnm · pm · (1 – p) n – m — вероятность того, что в n испытаниях событие Aпроизойдет m раз и не произойдет (n – m) раз; (1 – p) n — вероятность того, что в n испытаниях событие A не произойдет ни разу; — число сочетаний из n по m.

Математическое ожидание M биномиального распределения равно:

M = n · p,

где n — число испытаний, p — вероятность появления события A.

Среднеквадратичное отклонение σ:

σ = sqrt(n · p · (1 – p)).

Пример 1. Вычислить вероятность того, что событие, имеющее вероятность p = 0.5, в n = 10испытаниях произойдет m = 1 раз. Имеем: C ₁₀¹ = 10, и далее: P ₁ = 10 · 0.5¹ · (1 – 0.5)^{10 – 1} = 10 · 0.5¹⁰ = 0.0098. Как видим, вероятность наступления этого события достаточно мала. Объясняется это, во-первых, тем, что абсолютно не ясно, произойдет ли событие или нет, поскольку вероятность равна 0.5 и шансы здесь «50 на 50»; а во-вторых, требуется исчислить то, что событие произойдет именно один раз (не больше и не меньше) из десяти.

Пример 2. Вычислить вероятность того, что событие, имеющее вероятность p = 0.5, в n = 10испытаниях произойдет m = 2 раза. Имеем: C ₁₀² = 45, и далее: P ₂ = 45 · 0.5² · (1 – 0.5)^{10 – 2} = 45 · 0.5¹⁰ = 0.044. Вероятность наступления этого события стала больше!

Пример 3. Увеличим вероятность наступления самого события. Сделаем его более вероятным. Вычислить вероятность того, что событие, имеющее вероятность p = 0.8, в n = 10 испытаниях произойдет m = 1 раз. Имеем: C ₁₀¹ = 10, и далее: P ₁ = 10 · 0.8¹ · (1 – 0.8)^{10 – 1} = 10 · 0.8¹ · 0.2⁹ = 0.000004. Вероятность стала меньше, чем в первом примере! Ответ, на первый взгляд, кажется странным, но поскольку событие имеет достаточно большую вероятность, вряд ли оно произойдет только один раз. Более вероятно, что оно произойдет большее, чем один, количество раз. Действительно, подсчитывая P ₀, P ₁, P ₂, P ₃, …, P ₁₀ (вероятность того, что событие в n = 10 испытаниях произойдет 0, 1, 2, 3, …, 10 раз), мы увидим:

C ₁₀⁰ = 1, C ₁₀¹ = 10, C ₁₀² = 45, C ₁₀³ = 120, C ₁₀⁴ = 210, C ₁₀⁵ = 252,
C ₁₀⁶ = 210, C ₁₀⁷ = 120, C ₁₀⁸ = 45, C ₁₀⁹ = 10, C ₁₀¹⁰ = 1;

P ₀ = 1 · 0.8⁰ · (1 – 0.8)^{10 – 0} = 1 · 1 · 0.2¹⁰ = 0.0000…;
P ₁ = 10 · 0.8¹ · (1 – 0.8)^{10 – 1} = 10 · 0.8¹ · 0.2⁹ = 0.0000…;
P ₂ = 45 · 0.8² · (1 – 0.8)^{10 – 2} = 45 · 0.8² · 0.2⁸ = 0.0000…;
P ₃ = 120 · 0.8³ · (1 – 0.8)^{10 – 3} = 120 · 0.8³ · 0.2⁷ = 0.0008…;
P ₄ = 210 · 0.8⁴ · (1 – 0.8)^{10 – 4} = 210 · 0.8⁴ · 0.2⁶ = 0.0055…;
P ₅ = 252 · 0.8⁵ · (1 – 0.8)^{10 – 5} = 252 · 0.8⁵ · 0.2⁵ = 0.0264…;
P ₆ = 210 · 0.8⁶ · (1 – 0.8)^{10 – 6} = 210 · 0.8⁶ · 0.2⁴ = 0.0881…;
P ₇ = 120 · 0.8⁷ · (1 – 0.8)^{10 – 7} = 120 · 0.8⁷ · 0.2³ = 0.2013…;
P ₈ = 45 · 0.8⁸ · (1 – 0.8)^{10 – 8} = 45 · 0.8⁸ · 0.2² = 0.3020… (самая большая вероятность!);
P ₉ = 10 · 0.8⁹ · (1 – 0.8)^{10 – 9} = 10 · 0.8⁹ · 0.2¹ = 0.2684…;
P ₁₀ = 1 · 0.8¹⁰ · (1 – 0.8)^{10 – 10} = 1 · 0.8¹⁰ · 0.2⁰ = 0.1074…

Разумеется, P ₀ + P ₁ + P ₂ + P ₃ + P ₄ + P ₅ + P ₆ + P ₇ + P ₈ + P ₉ + P ₁₀ = 1.

Нормальное распределение

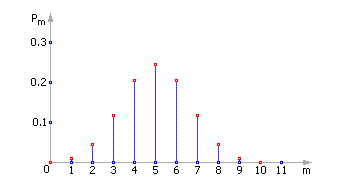
Если изобразить величины P ₀, P ₁, P ₂, P ₃, …, P ₁₀, которые мы подсчитали в примере 3, на графике, то окажется, что их распределение имеет вид, близкий к нормальному закону распределения (см. рис. 27.1) (см. лекцию 25. Моделирование нормально распределенных случайных величин).

Рис. 27.1. Вид биномиального распределения вероятностей для различных m при p = 0.8, n = 10

Биномиальный закон переходит в нормальный, если вероятности появления и непоявления события A примерно одинаковы, то есть, условно можно записать: p ≈ (1 – p). Для примера возьмем n = 10 и p = 0.5 (то есть p = 1 – p = 0.5).

Содержательно к такой задаче мы придем, если, например, захотим теоретически посчитать, сколько будет мальчиков и сколько девочек из 10 родившихся в роддоме в один день детей. Точнее, считать будем не мальчиков и девочек, а вероятность, что родятся только мальчики, что родится 1 мальчик и 9 девочек, что родится 2 мальчика и 8 девочек и так далее. Примем для простоты, что вероятность рождения мальчика и девочки одинакова и равна 0.5 (но на самом деле, если честно, это не так, см. курс «Моделирование систем искусственного интеллекта»).

Ясно, что распределение будет симметричное, так как вероятность рождения 3 мальчиков и 7 девочек равна вероятности рождения 7 мальчиков и 3 девочек. Наибольшая вероятность рождения будет у 5 мальчиков и 5 девочек. Эта вероятность равна 0.25, кстати, не такая уж она и большая по абсолютной величине. Далее, вероятность того, что родится сразу 10 или 9 мальчиков намного меньше, чем вероятность того, что родится 5 ± 1 мальчик из 10 детей. Как раз биномиальное распределение нам поможет сделать этот расчет. Итак.

C ₁₀⁰ = 1, C ₁₀¹ = 10, C ₁₀² = 45, C ₁₀³ = 120, C ₁₀⁴ = 210, C ₁₀⁵ = 252,
C ₁₀⁶ = 210, C ₁₀⁷ = 120, C ₁₀⁸ = 45, C ₁₀⁹ = 10, C ₁₀¹⁰ = 1;

P ₀ = 1 · 0.5⁰ · (1 – 0.5)^{10 – 0} = 1 · 1 · 0.5¹⁰ = 0.000977…;
P ₁ = 10 · 0.5¹ · (1 – 0.5)^{10 – 1} = 10 · 0.5¹⁰ = 0.009766…;
P ₂ = 45 · 0.5² · (1 – 0.5)^{10 – 2} = 45 · 0.5¹⁰ = 0.043945…;
P ₃ = 120 · 0.5³ · (1 – 0.5)^{10 – 3} = 120 · 0.5¹⁰ = 0.117188…;
P ₄ = 210 · 0.5⁴ · (1 – 0.5)^{10 – 4} = 210 · 0.5¹⁰ = 0.205078…;
P ₅ = 252 · 0.5⁵ · (1 – 0.5)^{10 – 5} = 252 · 0.5¹⁰ = 0.246094…;
P ₆ = 210 · 0.5⁶ · (1 – 0.5)^{10 – 6} = 210 · 0.5¹⁰ = 0.205078…;
P ₇ = 120 · 0.5⁷ · (1 – 0.5)^{10 – 7} = 120 · 0.5¹⁰ = 0.117188…;
P ₈ = 45 · 0.5⁸ · (1 – 0.5)^{10 – 8} = 45 · 0.5¹⁰ = 0.043945…;
P ₉ = 10 · 0.5⁹ · (1 – 0.5)^{10 – 9} = 10 · 0.5¹⁰ = 0.009766…;
P ₁₀ = 1 · 0.5¹⁰ · (1 – 0.5)^{10 – 10} = 1 · 0.5¹⁰ = 0.000977…

Разумеется, P ₀ + P ₁ + P ₂ + P ₃ + P ₄ + P ₅ + P ₆ + P ₇ + P ₈ + P ₉ + P ₁₀ = 1.

Отразим на графике величины P ₀, P ₁, P ₂, P ₃, …, P ₁₀ (см. рис. 27.2).

Рис. 27.2. График биномиального распределения при параметрах p = 0.5 и n = 10, приближающих его к нормальному закону

Итак, при условиях m ≈ n /2 и p ≈ 1 – p или p ≈ 0.5 вместо биномиального распределения можно использовать нормальное. При больших значениях n график сдвигается вправо и становится все более пологим, так как математическое ожидание и дисперсия возрастают с увеличением n: M = n · p, D = n · p · (1 – p).

Кстати, биномиальный закон стремится к нормальному и при увеличении n, что вполне естественно, согласно центральной предельной теореме (см. лекцию 34. Фиксация и обработка статистических результатов).

Теперь рассмотрим, как изменится биномиальный закон в случае, когда p ≠ q, то есть p –> 0. В этом случае применить гипотезу о нормальности распределения нельзя, и биномиальное распределение переходит в распределение Пуассона.

Распределение Пуассона

Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и при p –> 0 (редкие события)).

Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:

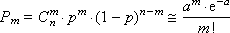
где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию. Приведем математические выкладки, поясняющие этот переход. Биномиальный закон распределения

P_m = C_n^m · p^m · (1 – p) ^{n – m}

может быть написан, если положить p = a / n, в виде

или

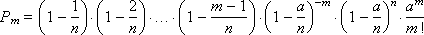
Так как p очень мало, то следует принимать во внимание только числа m, малые по сравнению с n. Произведение

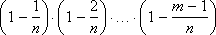
весьма близко к единице. Это же относится к величине

Величина

очень близка к e ^{– a} . Отсюда получаем формулу:

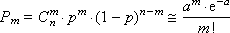
Пример. В ящике находится n = 100 деталей, как качественных, так и бракованных. Вероятность достать бракованное изделие составляет p = 0.01. Допустим, что мы вынимаем изделие, определяем, бракованное оно или нет, и кладем его обратно. Поступая таким образом, получилось, что из 100 изделий, которые мы перебрали, два оказались бракованными. Какова вероятность этого?

По биномиальному распределению получаем:

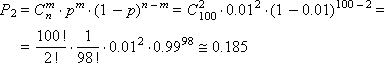
По распределению Пуассона получаем:

Как видно, величины получились близкими, поэтому в случае редких событий вполне допустимо применять закон Пуассона, тем более что он требует меньших вычислительных затрат.

Покажем графически вид закона Пуассона. Возьмем для примера параметры p = 0.05, n = 10. Тогда:

C ₁₀⁰ = 1, C ₁₀¹ = 10, C ₁₀² = 45, C ₁₀³ = 120, C ₁₀⁴ = 210, C ₁₀⁵ = 252,
C ₁₀⁶ = 210, C ₁₀⁷ = 120, C ₁₀⁸ = 45, C ₁₀⁹ = 10, C ₁₀¹⁰ = 1;

P ₀ = 1 · 0.05⁰ · (1 – 0.05)^{10 – 0} = 1 · 1 · 0.95¹⁰ = 0.5987…;
P ₁ = 10 · 0.05¹ · (1 – 0.05)^{10 – 1} = 10 · 0.05¹ · 0.95⁹ = 0.3151…;
P ₂ = 45 · 0.05² · (1 – 0.05)^{10 – 2} = 45 · 0.05² · 0.95⁸ = 0.0746…;
P ₃ = 120 · 0.05³ · (1 – 0.05)^{10 – 3} = 120 · 0.05³ · 0.95⁷ = 0.0105…;
P ₄ = 210 · 0.05⁴ · (1 – 0.05)^{10 – 4} = 210 · 0.05⁴ · 0.95⁶ = 0.00096…;
P ₅ = 252 · 0.05⁵ · (1 – 0.05)^{10 – 5} = 252 · 0.05⁵ · 0.95⁵ = 0.00006…;
P ₆ = 210 · 0.05⁶ · (1 – 0.05)^{10 – 6} = 210 · 0.05⁶ · 0.95⁴ = 0.0000…;
P ₇ = 120 · 0.05⁷ · (1 – 0.05)^{10 – 7} = 120 · 0.05⁷ · 0.95³ = 0.0000…;
P ₈ = 45 · 0.05⁸ · (1 – 0.05)^{10 – 8} = 45 · 0.05⁸ · 0.95² = 0.0000…;
P ₉ = 10 · 0.05⁹ · (1 – 0.05)^{10 – 9} = 10 · 0.05⁹ · 0.95¹ = 0.0000…;
P ₁₀ = 1 · 0.05¹⁰ · (1 – 0.05)^{10 – 10} = 1 · 0.05¹⁰ · 0.95⁰ = 0.0000…

Разумеется, P ₀ + P ₁ + P ₂ + P ₃ + P ₄ + P ₅ + P ₆ + P ₇ + P ₈ + P ₉ + P ₁₀ = 1.

Рис. 27.3. График распределения Пуассона при p = 0.05 и n = 10

При n –> ∞ распределение Пуассона переходит в нормальный закон, согласно центральной предельной теореме (см. лекцию 34. Фиксация и обработка статистических результатов).

Поток случайных событий

В предыдущих лекциях мы научились имитировать наступление случайных событий. То есть мы можем разыграть — какое из возможных событий наступит и в каком количестве. Чтобы это определить, надо знать статистические характеристики появления событий, например, такой величиной может быть вероятность появления события, или распределение вероятностей разных событий, если типов этих событий бесконечно много.

Но часто еще важно знать, когда конкретно наступит то или иное событие во времени.

Когда событий много и они следуют друг за другом, то они образуют поток. Заметим, что события при этом должны быть однородными, то есть похожими чем-то друг на друга. Например, появление водителей на АЗС, желающих заправить свой автомобиль. То есть, однородные события образуют некий ряд. При этом считается, что статистическая характеристика этого явления (интенсивность потока событий) задана. Интенсивность потока событий указывает, сколько в среднем происходит таких событий за единицу времени. Но когда именно произойдет каждое конкретное событие надо определить методами моделирования. Важно, что, когда мы сгенерируем, например, за 200 часов 1000 событий, их количество будет равно примерно величине средней интенсивности появления событий 1000/200 = 5 событий в час, что является статистической величиной, характеризующей этот поток в целом.

Интенсивность потока в некотором смысле является математическим ожиданием количества событий в единицу времени. Но реально может так оказаться, что в один час появится 4 события, в другой — 6, хотя в среднем получается 5 событий в час, поэтому одной величины для характеристики потока недостаточно. Второй величиной, характеризующей насколько велик разброс событий относительно математического ожидания, является, как и ранее, дисперсия. Собственно именно эта величина определяет случайность появления события, слабую предсказуемость момента его появления. Про эту величину мы расскажем в следующей лекции.

Итак.

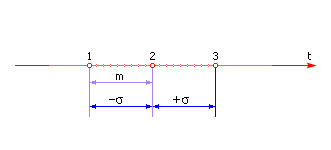
Поток событий — это последовательность однородных событий, наступающих одно за другим в случайные промежутки времени. На оси времени эти события выглядят как показано на рис. 28.1.

Рис. 28.1. Поток случайных событий

 

τj — интервал между событиями (случайная величина); t с i — момент совершения i -го события (отсчитывается от t = 0); T н — время наблюдения.

Примером потока событий могут служить последовательность моментов касания взлетной полосы самолетами, прилетающими в аэропорт.

Интенсивность потока λ — это среднее число событий в единицу времени. Интенсивность потока можно рассчитать экспериментально по формуле: λ = N / T _н, где N — число событий, произошедших за время наблюдения T _н.

Если интервал между событиями τ_j равен константе или определен какой-либо формулой в виде: t_j = f (t_{j – 1}), то поток называется детерминированным. Иначе поток называется случайным.

Случайные потоки бывают:

• ординарные: вероятность одновременного появления двух и более событий равна нулю;
• стационарные: частота появления событий λ (t) = const(t);
• без последействия: вероятность появления случайного события не зависит от момента совершения предыдущих событий.

Пуассоновский поток

За эталон потока в моделировании принято брать пуассоновский поток.

Пуассоновский поток — это ординарный поток без последействия.

Как ранее было указано, вероятность того, что за интервал времени (t ₀, t ₀ + τ) произойдет m событий, определяется из закона Пуассона:

где a — параметр Пуассона.

Если λ (t) = const(t), то это стационарный поток Пуассона (простейший). В этом случае a = λ · t. Если λ = var(t), то это нестационарный поток Пуассона.

Для простейшего потока вероятность появления m событий за время τ равна:

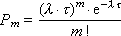
Вероятность непоявления (то есть ни одного, m = 0) события за время τ равна:

Рис. 28.2 иллюстрирует зависимость P ₀ от времени. Очевидно, что чем больше время наблюдения, тем вероятность непоявления ни одного события меньше. Кроме того, чем более значение λ, тем круче идет график, то есть быстрее убывает вероятность. Это соответствует тому, что если интенсивность появления событий велика, то вероятность непоявления события быстро уменьшается со временем наблюдения.

Рис. 28.2. График вероятности непоявления ни одного события во времени

Вероятность появления хотя бы одного события (P _ХБ1С) вычисляется так:

так как P _ХБ1С + P ₀ = 1 (либо появится хотя бы одно событие, либо не появится ни одного, — другого не дано).

Из графика на рис. 28.3 видно, что вероятность появления хотя бы одного события стремится со временем к единице, то есть при соответствующем длительном наблюдении события таковое обязательно рано или поздно произойдет. Чем дольше мы наблюдаем за событием (чем более t), тем больше вероятность того, что событие произойдет — график функции монотонно возрастает.

Чем больше интенсивность появления события (чем больше λ), тем быстрее наступает это событие, и тем быстрее функция стремится к единице. На графике параметр λ представлен крутизной линии (наклон касательной).

Рис. 28.3. График вероятности появления хотя бы одного события со временем

Если увеличивать λ, то при наблюдении за событием в течение одного и того же времени τ, вероятность наступления события возрастает (см. рис. 28.4). Очевидно, что график исходит из 0, так как если время наблюдения бесконечно мало, то вероятность того, что событие произойдет за это время, ничтожна. И наоборот, если время наблюдения бесконечно велико, то событие обязательно произойдет хотя бы один раз, значит, график стремится к значению вероятности равной 1.

Рис. 28.4. Влияние величины интенсивности потока на вероятность появления события в течение заданного интервала времени τ

Изучая закон, можно определить, что: m_x = 1/ λ, σ = 1/ λ, то есть для простейшего потока m_x = σ. Равенство математического ожидания среднеквадратичному отклонению означает, что данный поток — поток без последействия. Дисперсия (точнее, среднеквадратичное отклонение) такого потока велика. Физически это означает, что время появления события (расстояние между событиями) плохо предсказуемо, случайно, находится в интервале m_x – σ < τ_j < m_x + σ. Хотя ясно, что в среднем оно примерно равно: τ_j = m_x = T _н/ N. Событие может появиться в любой момент времени, но в пределах разброса этого момента τ_j относительно m_x на [– σ; + σ ] (величину последействия). На рис. 28.5 показаны возможные положения события 2 относительно оси времени при заданном σ. В данном случае говорят, что первое событие не влияет на второе, второе на третье и так далее, то есть последействие отсутствует.

Рис. 28.5. Иллюстрация влияния величины σ на положение события на временной шкале

По смыслу P равно r (см. лекцию 23. Моделирование случайного события. Моделирование полной группы несовместных событий), поэтому, выражая τ из формулы (*), окончательно для определения интервалов между двумя случайными событиями имеем:

τ = –1/ λ · Ln(r),

где r — равномерно распределенное от 0 до 1 случайное число, которое берут из ГСЧ, τ — интервал между случайными событиями (случайная величина τ_j).

Пример 1. Рассмотрим поток изделий, приходящих на технологическую операцию. Изделия приходят случайным образом — в среднем восемь штук за сутки (интенсивность потока λ = 8/24 [ед/час]). Необходимо промоделировать этот процесс в течение T _н = 100 часов. m = 1/ λ = 24/8 = 3, то есть в среднем одна деталь за три часа. Заметим, что σ = 3. На рис. 28.6 представлен алгоритм, генерирующий поток случайных событий.

Рис. 28.6. Алгоритм, генерирующий поток случайных событий в заданным λ

На рис. 28.7 показан результат работы алгоритма — моменты времени, когда детали приходили на операцию. Как видно, всего за период T _н = 100 производственный узел обработал N = 33 изделия. Если запустить алгоритм снова, то N может оказаться равным, например, 34, 35 или 32. Но в среднем, за K прогонов алгоритма N будет равно 33.33… Если посчитать расстояния между событиями t _{с i} и моментами времени, определяемыми как 3 · i, то в среднем величина будет равна σ = 3.

Рис. 28.7. Иллюстрация работы алгоритма, генерирующего поток случайных событий

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: