Представление информации в ЭВМ

Системы счисления

Системой счисления называется способ изображения чисел с помо­щью ограниченного набора символов, имеющих определенные количе­ственные значения. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора знаков (цифр).

Различают позиционные и непозиционные системы счисления. В по­зиционных системах каждая цифра числа имеет определенный вес, зависящий от позиции цифры в последовательности, изображающей чис­ло. Позиция цифры называется разрядом, В позиционной системе счис­ления любое число можно представить в виде

(2.1)

 

где: аi— i -я цифра числа;

k — количество цифр в дробной части числа;

т — количество цифр в целой части числа;

N — основание системы счисления.

Основание системы счисления N показывает, во сколько раз «вес» i-го разряда больше (i- 1) разряда. Целая часть числа отделяется от дробной части точкой (запятой).

Пример 2.1. A ₁₀=37.25.

В соответствии с формулой (2.1) это число формируется из цифр с весами разрядов:

A₁₀= 3●10¹ + 7●10°+2●10^-1 +5●10^-2.

Теоретически наиболее экономичной системой счисления является сис­тема с основанием е =2,71828..., находящимся между числами 2 и 3.

Во всех современных ЭВМ для представления числовой информации используется двоичная система счисления. Это обусловлено:

• более простой реализацией алгоритмов выполнения арифметических и логических операций;

• более надежной физической реализацией основных функций, так как они имеют всего два состояния (0 и 1);

• экономичностью аппаратной реализации всех схем ЭВМ.

При N=2 число различных цифр, используемых для записи чисел, ог­раничено множеством из двух цифр (нуль и единица). Кроме двоичной системы счисления широкое распространение получили и производные системы:

• двоичная—{0,1};

• десятичная, точнее, двоично-десятичное представление десятичных чисел— {О, 1,.... 9};

• шестнадцатеричная — {0, 1, 2,..., 9, А, В, С, D, Е, F}. Здесь шестнадца-теричная цифра А обозначает число 10, В — число 11,..., F — число 15;

• восьмеричная (от слова восьмерик) — {О, 1, 2, 3, 4, 5, 6, 7}. Она широко используется во многих специализированных ЭВМ. Восьмеричная и шестнадца-теричная системы счисления являются про­изводными от двоичной, так как 16 = 2⁴ и 8 = 2³. Они используются в ос­новном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков.

Пример 2.2. Число А₁₀ - 100.625 в двоичной, восьмеричной и шестнадцатеричной системах счисления имеет следующее представление:

A₂= 1100100.101;

А₈ = 144.5;

А₁₆ = 64.А;

А₂ = 1● 2⁶+1● 2⁵+0 • 2⁴+ 0 • 2³+1● 2²+0 •2¹+1●2°+1● 2^-1+0 • 2^-2+1● 2^-3;

A₈ =1●8²+4●8¹+4●8°+5●8^-1;

А₁₆ = 6 • 16¹+4● 16⁰+10● 16^-1.

Представление чисел в различных системах счисления допускает однозначное преобразование их из одной системы в другую. В ЭВМ перевод из одной системы в другую осуществляется автоматически, по специальным программам. Правила перевода целых и дробных чисел отличаются.

 

Перевод целых чисел.

Целое число с основанием N_l переводится в систему счисления с основанием N₂ путем последовательного деления числа A_n1, на основание N₂, записанного в виде числа с основанием N ₁, до получения остатка. Полученное частное следует вновь делить на основание N₂, и этот процесс надо повторять до тех пор, пока частное не станет меньше делителя. Полученные остатки от деления и последнее частное записываются в порядке, обратном полученному при делении. Сформированное число и будет являться числом с основа­нием N₂.

A₁₀=37 A₁₀=37

А₂= 100101 А₁₆ = 25

 

Перевод дробных чисел

Дробное число с основанием N₁ переводится в систему счисления с основанием N₂ путем последовательного умножения A_N1 на осно­вание N₂, записанное в виде числа с основанием N₁. При каждом умножении целая часть произведения берется в виде очередной цифры соответствующего разряда, а оставшаяся дробная часть принимается за новое множимое. Число умножений определяет разрядность по­лученного результата, представляющего число A_N1 в системе счис­ления N₂.

Пример 2.4. A₁₀= 0,625; A₂ =?; A ₁₆ =?

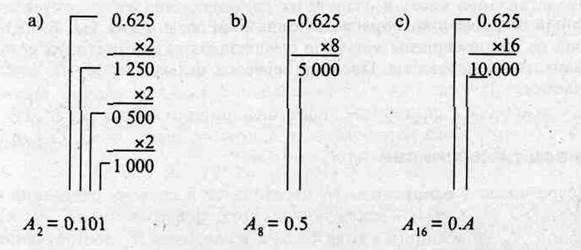
Так как двоичная, восьмеричная и шестнадцатеричная системы связаны через степени числа 2, то преобразования между ними можно выполнять другим, более простым, способом. Для перевода из шестнадцатеричной (восьмеричной) системы счисления в двоичную достаточно двоичным кодом записать шестнадцатеричные коды цифр тетрадами (по 4 двоичных разряда) и триадами (по 3 двоичных разряда) — для восьмеричных цифр. Обратный перевод из двоичного кода производится в обратном порядке: двоичное число разбивается влево и вправо от границы целой и дробной частей: на тетрады — для последующей записи цифр в шестнадцатеричном представлении; на триады — для записи их значений восьмеричными цифрами.

Представление информации в ЭВМ

Информация — это сведения об окружающем мире и протекающих в нем процессах, воспринимаемые человеком или специализированным устройством, например ЭВМ, для обеспечения целенаправленной деятельности.

Информация может быть по своей физической природе: числовой, текстовой, графической, звуковой, видео и др. Она также может быть постоянной (не меняющейся), переменной, случайной, вероятностной. Наибольший интерес представляет переменная информация, так как она позволяет выявлять причинно-следственные связи в процессах и явлениях. Существуют различные способы оценки количества инфор­мации. Классическим является подход, использующий формулу К.Шеннона. Применительно к двоичной системе она имеет вид

H = log₂N,

где: Н — количество информации, несущей представление о состоянии, в котором находится объект;

N — количество равновероятных альтернативных состояний объекта.

Любая информация, обрабатываемая в ЭВМ, должна быть пред­ставлена двоичными цифрами {0,1}, т.е. должна быть закодирована ком­бинацией этих цифр. Различные виды информации (числа, тексты, гра­фика, звук) имеют свои правила кодирования. Коды отдельных значе­ний, относящиеся к различным видам информации, могут совпадать. Поэтому расшифровка кодированных данных осуществляется по кон­тексту при выполнении команд программы.

123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: