 |
Понятие о минимизации логических функций
|
|
|
|
Проблема минимизации логических функций решается на основе применения законов склеивания и поглощения с последующим перебором получаемых дизъюнктивных форм и выбором из них оптимальной (минимальной). Существует большое количество методов минимизации ЛФ. Все они отличаются друг от друга спецификой применения операций склеивания и поглощения, а также различными способами сокращения переборов. Среди аналитических методов наиболее известным является метод Квайна — МакКласки, среди табличных — метод с применением диаграмм Вейча [6]. Графические методы минимизации отличаются большей наглядностью и меньшей трудоемкостью, однако их применение эффективно при малом числе переменных n≤5.
Рассмотрим последовательность действий минимизации ЛФ на примере.
Пример 2.15. Найти минимальную дизъюнктивную форму функции, заданной таблицей истинности (табл. 2.6).
Таблица 2.6 Таблица истинности функции У=f(x1, x2, x3)
| Х1 | Х2 | Xз | Y |
Эта функция интересна тем, что имеет несколько минимальных форм. По данным таблицы запишем аналитическое выражение: 
Пунктирными линиями в этом выражении отмечены пары конъюнкций, к которым можно применить операцию склеивания типа Fx V Fx =F. Особенно хорошо это видно при использовании диаграммы Вейча, в которой «склеиваемые» конъюнкции находятся по соседству друг с другом. Диаграмма Вейча просто по-другому интерпретирует таблицу истинности (табл. 2.7).
Та б л и ц а 2.7 Диаграмма Вейча функции у
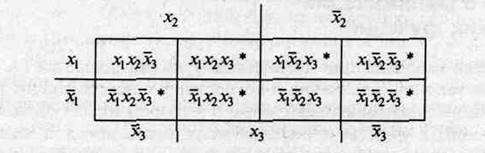
После выделения конъюнкций (они отмечены звездочкой), видно, какие конъюнкции могут образовывать пары для склеивания.
|
|
|
В результате применения операций склеивания и поглощения можно получить другое аналитическое выражение:

в котором отсутствуют возможности дальнейших склеиваний и поглощений. Однако последнее выражение является избыточным, так как отдельные конъюнкции могут быть «лишними», т.е. их «составные части» могут включаться в другие конъюнкции. У данной функции существует пять безызбыточных дизъюнктивных форм, из которых только две являются минимальными:

Из приведенных зависимостей видно, что только функции у1 и у4 являются минимальными формами функций, так как они содержат наименьшее число конъюнкций и имеют минимальный ранг этих конъюнкций.
Минимизация «вручную» возможна только для функций, зависящих от 4—5 переменных, так как трудоемкость переборов растет в квадратичной зависимости от числа переменных. Применение мощных ЭВМ для этих целей позволяет расширить границы до n=12—15. Если при этом учесть, что функции могут быть частично определены (значения функций на некоторых наборах переменных можно определять произвольно), а также, что иногда приходится решать задачи совместной минимизации систем ЛФ, то минимизация ЛФ становится сложной инженерной, практической и научной проблемой.
Техническая интерпретация
Логических функций
По логическим выражениям проектируются схемы ЭВМ. При этом надо придерживаться определенной последовательности действий.
1. Словесное описание работы схемы.
2. Формализация словесного описания.
3. Запись функций в дизъюнктивной (конъюнктивной) совершенной нормальной форме по таблицам истинности.
4. Минимизация логических зависимостей с целью их упрощения.
5. Представление полученных выражений в выбранном логически полном базисе элементарных функций.
6. Построение схемы устройства.
|
|
|
7. Проверка работоспособности полученной схемы. Покажем взаимосвязь перечисленных этапов на примере.
Пример 2.16. Спроектировать схему, фиксирующую появление «неправильной» тетрады в двоично-десятичном представлении чисел.
1. Каждая тетрада двоично-десятичного представления числа содержит десятичные цифры 0—9, что соответствует двоичным числам 0000—1001. Значения тетрады, соответствующие двоичным числам 1010—1111 (шестнадцатеричные цифры А—F), не должны появляться при представлении десятичных чисел.
2. Составим таблицу истинности функции (табл. 2.8), которая принимает значения, равные единице, при появлении «неправильных» тетрад. Разряды тетрады обозначим переменными х, у, z, и.
Таблица 2.8 Таблица истинности функции F

3. Исходная совершенная дизъюнктивная нормальная форма записы вается как

4. Эта форма функции допускает упрощение, что видно по диаграмме Вейча (табл.2.9). Этот же результат может быть получен аналитически.
Таблица 2.9 Диаграмма Вейча для функции F
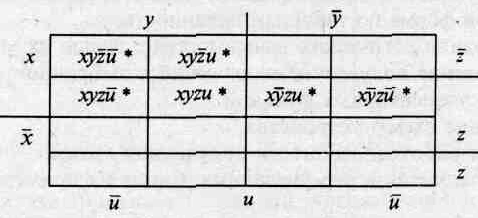
5. Минимальная форма функции F в логически полном базисе {&, v, [} будет иметь вид:

Для представления этой же схемы в другом полном базисе, например {& }, воспользуемся правилом де Моргана:

6. По полученным зависимостям можно построить схемы фиксации «неправильных» тетрад (рис. 2.2).
7. Проверить работоспособность построенных схем можно путем задания различных комбинаций переменных х, у, z, и и определения реакции на выходе схемы F.

Рис. 2.2. Схема фиксации «неправильных» тетрад:
а — схема в базисе ([, &, v),
б — схема в базисе (&)
Контрольные вопросы
1.Что понимается под системой счисления?
2. Сформулируйте правила перевода целых и дробных чисел из одной системы счисления в другую.
3. Как переводятся числа в системах счисления с основаниями, кратными степени 2?
4. В чем заключается различие между представлениями чисел в формах с фиксированной и плавающей точкой (запятой)?
5. Каким образом представляется в ЭВМ текстовая и графическая информация?
6. Каково назначение обратного и дополнительного кодов? Каково назначение модифицированных обратного и дополнительного кодов?
7. Приведите примеры выполнения арифметических операций над числами с фиксированной и плавающей точкой.
|
|
|
8. Как выполняются операции над двоично-кодированными десятичными числами? В чем сущность проведения коррекций?
9. Что понимается под логическими функциями?
10. Приведите примеры выполнения логических операций над двоичными кодами.
11. Что понимается под термином «минимизация логических выражений»?
12. Что такое логически полный базис?
13. Какова связь логических выражений со схемами ЭВМ?
|
|
|


