Определение реакций в кинематических парах

 

Определение реакций в кинематических парах начинаем с рассмотрения равновесия группы Ассура (2-3).

На звенья этой группы действуют силы: движущая сила F_д, силы тяжести G ₃, G ₂, результирующие силы инерции Ф _{u 3}, Ф_u2, реакция R ₀₃, заменяющая действие стойки 0 на ползун 3 и реакция R ₁₂, заменяющая действие кривошипа 1 на шатун 2.

Силы, приложенные в точке B, приводим к одной силе F ₃. Величину этой силы определяем по формуле:

(41)

F₃=+___+___+___=____ Н.

Знак (+) показывает, что сила F ₃ направлена вверх.

Условие равновесия группы (2-3) выражается следующим образом:

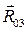+ + + + =0. (42)

Реакцию R ₁₂ раскладываем на две составляющие: R – действующая вдоль оси звена AB и R – перпендикулярно звену AB.

Составляющую R определяем из уравнения суммы моментов всех внешних сил относительно точки B, действующих на шатун AB.

Применительно к рассматриваемой схеме механизма это уравнение можно записать так:

R × l₂-Ф_u2×h₁-G₂×h₂=0, (43)

откуда

R =(Ф_u2×h₁+G₂×h₂)l₂; (44)

R = (__×__+__×__)___=____ Н.

План сил (42) строим в масштабе: m_F =___ Н/мм.

Из произвольной точки Р последовательно откладываем вектора R , F ₃+ G ₂, Ф_u2. Через конечную точку вектора Ф_u2 проводим линию действия реакции R ₀₃, а через начальную точку вектора R -линию действия силы R . Получим точку пересечения. Соединив конечную точку вектора Ф_u2 с точкой пересечения, получим вектор R ₀₃. Соединив точку пересечения с конечной точкой вектора R , получим вектор R ₁₂.Умножив соответствующие длины на масштабный коэффициент, получим: R ₀₃ = _ H; R ₁₂ = _ H.

По результатам расчета программы ТММ1 строим годограф реакции R ₁₂ в масштабе m_R =_ Н/мм.

Если в каждом из двенадцати положений ползуна отложить вектор R ₀₃ и соединить их конечные точки плавной кривой, то получим годограф реакции R ₀₃.

По результатам расчета программы ТММ1 строим годограф реакции R ₀₃= R ₀₃(S_B) в масштабе m_R =_Н/мм, m_S =_м/мм.

Реакцию R ₃₂ в паре шатун – ползун определяем из условия равновесия ползуна:

+ + =0 (45)

и равенства:

, (46)

или

(47)

Тогда

R_23X =R₀₃ =_ H;

R_23Y =F₃ =_ H;

R₂₃= (48)

R₂₃= =_ Н;

R₃₂ =_ Н.

По результатам расчета программы ТММ1 строим диаграмму реакции R ₃₂= R ₃₂(j ₁) в масштабе: m_R =__ Н/мм.

 

 

Силовой расчет механизма 1 класса

К кривошипу приложена сила тяжести G ₁, известная реакция . Неизвестная по значению и направлению реакция R ₀₁:

Чтобы кривошип мог совершать вращение по заданному закону, к нему со стороны отделенной части машинного агрегата должна быть приложена реактивная нагрузка в виде уравновешивающей силы F_y. Допустим, что неизвестная по модулю уравновешивающая сила приложена перпендикулярно кривошипу в точке А.

 

Определение сил тяжести

Силу тяжести кривошипа определяем по формуле:

G₁=m₁×g, (49)

где m ₁ – масса кривошипа;

g – ускорение силы тяжести.

G₁=_×9,81=_ Н.

Определение реакций в кинематических парах

Реакция R ₀₁ в паре кривошип-стойка и уравновешивающий момент M_y определяем из условия равновесия кривошипа ОА:

=0. (50)

Силу F_y находим из условия:

F_y× l₁ –R₂₁×h₃=0. (51)

Откуда

F_y=R₂₁×h₃/l₁; (52)

F_y=_×_/_=_ Н.

План сил строим в масштабе: m_F =_ Н/мм.

Из произвольной точки последовательно откладываем вектора R ₂₁, G ₁. Соединив конечную точку вектора G ₁ с начальной точкой вектора R _21, получим вектор R ₀₁. Умножив полученную длину на масштабный коэффициент, получим: R ₀₁=___Н. По результатам расчета программы ТММ1 строим диаграмму реакции R ₀₁= R ₀₁(j ₁) в масштабе m_R =__ Н/мм.

Уравновешивающий момент M_y определяется по формуле:

M_y=F_y×l₁; (53)

M_y=_×_=_Н×м.

По результатам расчета программы ТММ1 строим диаграмму уравновешивающего момента M_у = M_у (j ₁) в масштабе: m_M =___ Н×м/мм.

Рычаг Жуковского

С целью проверки правильности силового расчета механизма уравновешивающий момент M_y определяем с помощью рычага Жуковского.

На план скоростей, предварительно повёрнутый на 90 градусов вокруг полюса, в соответствующие точки переносим все заданные силы, включая силы инерции и уравновешивающую силу F_y. Из условия равновесия плана скоростей, как рычага, определяем уравновешивающую силу F_y, прикладывая ее в точке a, считая ее как бы приложенной в точке A кривошипа, и направляем перпендикулярно линии кривошипа ОА.

Таким образом:

F_y×Pa+Ф_u2×h₄+G₂×h₅-F₃×Pb=0. (54)

Откуда:

F_y=(- Ф_u2×h₄-G₂×h₅+F ×Pb)/Pa; (55)

F =(__×__ - __×__ + __×__)/___=____ Н.

Определяем величину уравновешивающего момента:

M =F ×l ; (56)

M =__×__=___ Н×м.

Таблица 3

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: