 |
Методические рекомендации к выполнению контрольной работы №2
|
|
|
|
Методические рекомендации к выполнению контрольной работы №2
Указания к решению задач № 1 и №2
В контрольную работу №2 входят задачи по трехфазным цепям переменного тока. Расчет цепей переменного тока базируется на знании законов Ома и Кирхгофа, особенностей этих цепей в связи с фазовыми сдвигами, которые вызываются реактивными сопротивлениями. По этой причине уравнения по законам Кирхгофа будут справедливы в векторной форме; а при определении модулей векторов приходится прибегать к помощи геометрических и тригонометрических выражений.
Типовой пример к задаче №1
Трехфазная цепь, изображенная на рис. 15, подключена в линию с линейным напряжением UЛ = 380 В. Известны сопротивления, включенные в фазы: R1=R2=Rз =12 Ом; ХC=9 ХL = 5 Ом.
Определить линейные токи и полную мощность цепи; построить в масштабе векторную диаграмму и объяснить ее построение.
Рис. 15
Решение
1. Определяем полное сопротивление фаз:
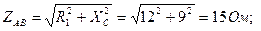
ZCA=R3= 12 Ом.
2. Определим фазные токи:
3. Определим углы сдвига фаз напряжения и тока в каждой фазе:
4. Активные мощности фаз и всей цепи:
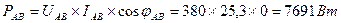
5. Реактивные мощности фаз и всей цепи:
5. Полные мощности фаз и всей цепи:
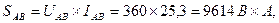
7. Строим векторную диаграмму напряжений и токов (рис. 16):
- принимаем масштабы: МU = 76 В/см; МI = 10 А/см;
- первым строим векторы фазных (они же линейные) напряжений в виде треугольника в целях компактного расположения; при таком расположении векторов углы сдвигов между фазами 120° соблюдаются, в чем легко убедиться, если все векторы мысленно совместить своими началами;
|
|
|
- строим векторы фазных токов с учетом сдвигов между напряжением и током в каждой фазе цепи. Ток в фазе АВ опережает напряжение ( 
вследствие наличия емкости в этой фазе, поэтому вектор IАВ строим левее (против хода часовой стрелки) вектора UАВ; ток в фазе ВС отстает от напряжения 
вследствие наличия индуктивности в этой фазе, поэтому вектор Iвс строим правее вектора UВС; ток в фазе СА совпадает по фазе с напряжением 
, поэтому вектор IСА строим вдоль вектора UСА в том же направлении;
- строим векторы линейных токов на основе векторных уравнений, связывающих линейные и фазные токи в каждом узле цепи:
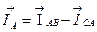
Эти уравнения составлены согласно 1-му закону Кирхгофа с учетом направлений токов относительно узлов а, b, с. Векторы линейных токов строятся как замыкающие двух векторов фазных токов, один из которых обратный (рис. 16). Обратные векторы на диаграмме показаны пунктиром.
Рис. 16
7. Определяем величины токов с помощью векторной диаграммы:
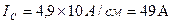
Типовой пример к задаче №2
Для схемы цепи, приведенной на рис. 17, начертить в масштабе векторную диаграмму и определить графически ток в нулевом проводе. Как изменится этот ток при отключении линейного провода А? Линейное напряжение сети UЛ = 380 В.
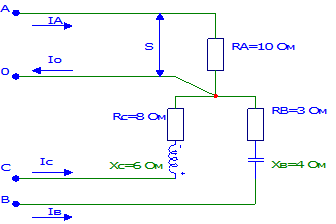
Рис. 17
Решение
1. Полное сопротивление фаз:
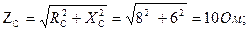
2. Фазные (они же линейные) токи:
,
,
.
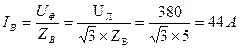3. Углы сдвига фаз между током и фазным напряжением в каждой фазе:
4. Построение векторной диаграммы начинаем с векторов фазных напряжений UА, UВ, UС (рис. 18), располагая их под углом 120° относительно друг друга. Чередование фаз принято обычным: за фазой А фаза В, за фазой В - фаза С. Под углами φ А, φ В, φ С к соответствующим векторам фазных напряжений откладываем векторы линейных токов IА, IВ, IС.
|
|
|
Их геометрическая сумма равна току в нулевом проводе,
I0 = 48А. При построении векторной диаграммы были приняты масштабы:
МU = 50 В/см, MI = 10 А/см.
Ток в фазе А совпадает с фазным напряжением UA 
; ток в фазе В опережает фазное напряжение Uв 
; ток в фазе С отстает от фазного напряжения Uс 
.
На этой же диаграмме показаны векторы линейных напряжений UАВ, UBC, UCA.
При отключении линейного провода А линейный ток IA =0, а токи IВ и IC не меняют своей величины. Ток в нулевом проводе в этом случае равен геометрической сумме токов IВ и IС (см. построение на рис. 18). Из диаграммы графически находим: I0 =30 A.
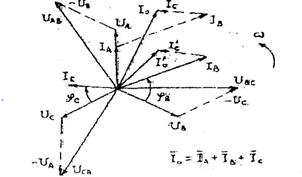Рис. 18
|
|
|
