 |
Использование решателей систем ОДУ
|
|
|
|
В описанных далее функциях для решения систем ДУ приняты следующие обозначения и правила:
• tspan вектор, определяющий интервал интегрирования [ t 0 tfinal ]. Для получения решений в конкретные моменты времени t 0, t 1, …, tfinal (расположенные в порядке уменьшения или увеличения) нужно использовать tspan = [ t 0 t 1 … tfinal ];
• y 0 вектор начальных условий;
• options аргумент, создаваемый функцией odeset (еще одна функция odeget или bvpget (только для bvp4c) позволяет вывести параметры, установленные по умолчанию или с помощью функции odeset/bvpset);
• p 1, p 2,… произвольные параметры, передаваемые в функцию F;
• T, Y матрица решений Y, где каждая строка соответствует времени, возвращенном в векторе-столбце T.
Перейдем к описанию синтаксиса функций для решения систем ДУ (под именем solver подразумевается любая из представленных выше функций).
• [ T, Y ]=solver(@ F, tspan, y 0) интегрирует систему ДУ вида y ′ = F (t, y) на интервале tspan с начальными условиями y 0. @ F дескриптор ОДУ-функции (можно также задавать функцию в виде ' F '). Каждая строка в массиве решений Y соответствует значению времени, возвращаемому в векторе-столбце T.
• [ T, Y ]=solver(@ F, tspan, y 0,options) дает решение, подобное описанному выше, но с параметрами, определяемыми значениями аргумента options, созданного функцией odeset. Обычно используемые параметры включают допустимое значение относительной погрешности RelTol (по умолчанию 1e3) и вектор допустимых значений абсолютной погрешности AbsTol (все компоненты по умолчанию равны 1e6).
• [ T, Y ]=solver(@ F, tspan, y 0,options, p 1, p 2…) дает решение, подобное описанному выше, передавая дополнительные параметры p 1, p 2, … в m -файл F всякий раз, когда он вызывается. Используйте options=[], если никакие параметры не задаются.
|
|
|
Решение ОДУ первого порядка
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучить теоретическую часть. Выполните задания, соответствующие номеру Вашего варианта, и продемонстрируйте их преподавателю.
2. Оформите отчет по лабораторной работе, который должен содержать:
· титульный лист;
· исходные данные варианта;
· решение задачи;
· результаты решения задачи.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Пример
Найти решение дифференциального уравнения 
на отрезке [1,7; 2,7], для которого у (1,7) = 5,3.
Создаем в Command Window функция пользователя
g=@(x,y)[x-cos(y/pi)];
В синтаксисе функции @(x,y) x независимая переменная, y зависимая переменная, x -cos(y / pi) правая часть ДУ.
Процесс решения осуществляется обращением в Command Window к решателю (солверу) следующим оператором:
[x,ya]=ode23(g,[1.7,2.7],[5.3]);
Построение графика с сеткой осуществляется следующими операторами:
plot(x,ya)
grid on
Результат представлен на рис. 1.1
Рис. 1.2.1. Визуализация численного решения
ЗАДАНИЕ
1. Найдите решения ДУ первого порядка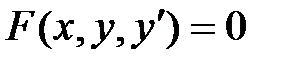 
, удовлетворяющего начальным условиям у(х 0 ) = у 0 на промежутке [ a, b ].
2. Построить графики функции.
Варианты заданий.
| № варианта | 
| у(х 0 )=у 0 | [ a, b ] |
| y 0(1,8)=2,6 | [1,8; 2,8] | |
| y 0(0,6)=0,8 | [0,6; 1,6] | |
| y 0(2,1)=2,5 | [2,1; 3,1] | |
| y 0(0,5)=0,6 | [0,5; 1,5] | |
| y 0(1,4)=2,2 | [1,4; 2,4] | |
| y 0(1,7)=5,3 | [1,7; 2,7] | |
| y 0(1,4)=2,5 | [1,4; 2,4] | |
| y 0(1,6)=4,6 | [1,6; 2,6] | |
| y 0(1,8)=2,6 | [1,8; 2,8] | |
| y 0(1,7)=5,3 | [1,7; 2,7] | |
| y 0(0,4)=0,8 | [0,4; 1,4] | |
| y 0(1,2)=1,4 | [1,2; 2,2] |
Лабораторная работа № 2
Решение систем ОДУ
ЦЕЛЬ РАБОТЫ
Сформировать у студентов представления о применении систем ДУ в различных областях; привить умения решать задачу Коши для систем ДУ.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучить теоретическую часть. Выполните задания, соответствующие номеру Вашего варианта, и продемонстрируйте их преподавателю.
|
|
|
2. Оформите отчет по лабораторной работе, который должен содержать:
· титульный лист;
· исходные данные варианта;
· решение задачи;
· результаты решения задачи.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Пример
Решить систему 
при данных начальных условиях 
с использованием решателя ode23().
Решение:
1. Создать в редакторе m-файл функции вычисления правых частей ДУ.
Пусть имя в редакторе файла sisdu.m, тогда функция может иметь следующий вид:
function z=sisdu(t,y)
z1=-3*y(2)+cos(t)-exp(t);
z2=4*y(2)-cos(t)+2*exp(t);
z=[z1;z2];
Следует иметь в виду, что для того чтобы MATLAB работал корректно необходимо придерживаться следующих правил.
Исполняемая функция и обращающаяся к ней программа (m-файл) должны находится в папке пользователя. Эту папку следует предварительно создать и указать путь к ней.
Это осуществляется в несколько шагов.
На первом шаге в папке Мои документы создаем папку с названием группы.
Затем, в Command Window MATLAB через пиктограмму обозревателя (сразу справа от окна указателя рабочего каталога) находим созданную папку и нажимаем ОК. В окне указателя рабочего каталога должен появиться адрес этой рабочей папки.
Сохраняем созданную функцию в этой папке.
2. Выполнить следующие действия:
>> t0=0;tf=5;y0=[-3/17,4/17];
>> [t,y]=ode23('sisdu',[t0,tf],y0);
>> plot(t,y)
>>grid on
Рис. 1.3.1. Визуализация численного решения, полученного с помощью функции ode23.
ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ
1. Что значит решить задачу Коши для системы ДУ?
2. Какие существуют методы решения систем ДУ?
ЗАДАНИЕ
1. Найдите решение системы ДУ
удовлетворяющее начальным условиям 
на промежутке [0, 1];
2. Построить графики функций.
Для примера приводится функция решения 8-го варианта:
function z=ssisdu(t,y)
% вариант 8
a=0.8;m=2.7;
z1=-a*y(1)+a*y(2);
z2=a*y(1)-(a-m)*y(2)+2*m*y(3);
z3=a*y(2)-(a-m)*y(3)+3*m*y(4);
z4=a*y(3)-3*m*y(4);
z=[z1;z2;z3;z4];
>> [t,y]=ode23('ssisdu',[0 1],[1 0 0 0]);
>> plot(t,100*y)
>>grid on
Рис. 1.3.2. Визуализация численного решения, полученного с помощью функции ode23.
Варианты заданий.
| № варианта | Задания | |
| a | m | |
| 0,1 | 1,2 | |
| 0,2 | 1,5 | |
| 0,3 | 1,7 | |
| 0,4 | 1,9 | |
| 0,5 | ||
| 0,6 | 1,9 | |
| 0,7 | 2,3 | |
| 0,8 | 2,7 | |
| 0,9 | ||
| 0,1 | 1,5 | |
| 0,2 | 1,1 | |
| 0,3 |
|
|
|
Лабораторная работа № 3
1.4Решение ОДУ n -го порядка
ЦЕЛЬ РАБОТЫ
Сформировать у студентов представления о применении ДУ высших порядков в различных областях; привить умения решать задачу Коши для ДУ высших порядков с помощью прикладных программ; развить навыки проверки полученных результатов.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучить теоретическую часть. Выполните задания, соответствующие номеру Вашего варианта, и продемонстрируйте их преподавателю.
2. Оформите отчет по лабораторной работе, который должен содержать:
· титульный лист;
· исходные данные варианта;
· решение задачи;
· результаты решения задачи.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Пример 1.
Решить ДУ второго порядка 
при данных начальных условиях 
.
Решение:
Сначала приведем ДУ к системе:
1. Создать m-файл функции вычисления правых частей ДУ.
Пусть имя файла sisdu_3.m, тогда функция может иметь следующий вид:
function z=sisdu_3(x,y)
z1=y(2);
z2=6*x*exp(x)+2*y(2)+y(1);
z=[z1;z2];
2. Выполнить следующие действия:
>> x0=0;xf=10;y0=[0,1];
>> [x,y]=ode23('sisdu_3',[x0,xf],y0);
>> plot(x,y(:,1))
>>grid on
Рис. 1.4.1. Визуализация численного решения, полученного с помощью функции ode23.
ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ
1. Что значит решить задачу Коши для ДУ высших порядков?
2. Как привести ДУ m -го порядка к системе ДУ?
ЗАДАНИЕ
1. Найдите решение ДУ, удовлетворяющее начальным условиям на промежутке [0, 10].
2. Построить графики функций.
Варианты заданий.
| № варианта | Задания | |
| Уравнения | Начальные условия | |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
|
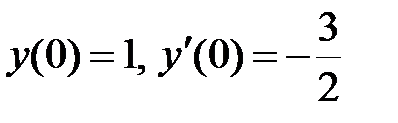
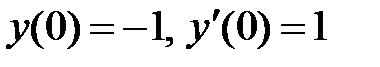
Лабораторная работа № 4 – 5
Динамические системы (ДС)
ЦЕЛЬ РАБОТЫ
Знакомство студентов с основными понятиями ДС, их классификация, фазовое пространство ДС, кинематическая интерпретация системы ДУ, эволюция ДС. Уравнение движения маятника. Динамика осциллятора Ван дер Поля.
2. Динамическая система (ДС) математический объект, соответствующий реальным системам (физическим, химическим, биологическим и др.), эволюция которых однозначно определяется начальным состоянием. ДС определяется системой уравнений (дифференциальных, разностных, интегральных и т.д.), допускающих существование на бесконечном интервале времени единственность решения для каждого начального условия.
|
|
|
Состояние ДС описывают набором переменных, выбираемых из соображений естественности их интерпретации, простоты описания, симметрии и т.п. Множество состояний ДС образует фазовое пространство, каждому состоянию отвечает точка в нём, а эволюция изображается (фазовыми) траекториями. Чтобы определить близость состояний, в фазовом пространстве ДС вводят понятие расстояния. Совокупность состояний в фиксированный момент времени характеризуется фазовым объёмом.
Описание ДС в смысле задания закона эволюции также допускает большое разнообразие: оно осуществляется с помощью дифференциальных уравнений, дискретных отображений, с помощью теории графов, теории марковских цепей и т.д. Выбор одного из способов описания задает конкретный вид математической модели соответствующей ДС.
Математическая модель ДС считается заданной, если введены динамические переменные (координаты) системы, определяющие однозначно ее состояние, и указан закон эволюции состояния во времени.
В зависимости от степени приближения одной и той же системе могут быть поставлены в соответствие различные математические модели. Исследование реальных систем идет по пути изучения соответствующих математических моделей, совершенствование и развитие которых определяется анализом экспериментальных и теоретических результатов при их сопоставлении. В связи с этим под динамической системой мы будем понимать именно ее математическую модель. Исследуя одну и ту же ДС (к примеру, движение маятника), в зависимости от степени учета различных факторов мы получим различные математические модели.
|
|
|
