 |
Кинематическая интерпретация системы ДУ
|
|
|
|
Рассмотрим ДС, моделируемые конечным числом обыкновенных дифференциальных уравнений (ОДУ). Применительно к таким системам сохранились представления и терминология, первоначально возникшие в механике. В рассматриваемом случае для определения ДС необходимо указать объект, допускающий описание состояния заданием величин x 1, x 2, …, xn в некоторый момент времени t = t 0. Величины xi могут принимать произвольные значения, причем двум различным наборам величин xi и xi ’ отвечают два разных состояния. Закон эволюции динамической системы во времени описывается системой ОДУ
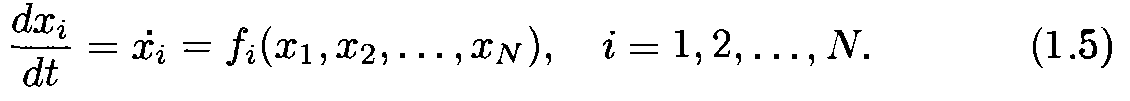
Если рассматривать величины х 1, х 2,..., xN как координаты точки x в N -мерном пространстве, то получается наглядное геометрическое представление состояния динамической системы в виде этой точки. Последнюю называют изображающей, а чаще фазовой точкой, а пространство состояний фазовым пространством динамической системы. Изменению состояния системы во времени отвечает движение фазовой точки вдоль некоторой линии, называемой фазовой траекторией. В фазовом пространстве системы уравнениями (1.5) определяется векторное поле скоростей, сопоставляющее каждой точке x выходящий из нее вектор скорости F (x), компоненты которого даются правыми частями уравнений (1.5):
Динамическая система (1.5) может быть записана в векторной форме:
где F (x) вектор-функция размерности N. Необходимо уточнить взаимосвязь понятий числа степеней свободы и размерности фазового пространства динамической системы. Под числом степеней свободы понимается наименьшее число независимых координат, необходимых для однозначного определения состояния системы. Под координатами первоначально понимались именно пространственные переменные, характеризующие взаиморасположение тел и объектов. В то же время для однозначного решения соответствующих уравнений движения необходимо, помимо координат, задать соответствующие начальные значения импульсов или скоростей. В связи с этим система с n степенями свободы характеризуется фазовым пространством размерности в два раза большей (Ν = 2 n).
|
|
|
2.4. Эволюция ДС. Качественные особенности эволюции ДС проявляются в характере фазовых траекторий. Например, состоянию равновесия отвечает вырожденная траектория точка в ФП, периодическому движению замкнутая траектория. Траектория квазипериодического движения с т несоизмеримыми частотами wi (т.е. такими, что не существует отличных от нуля целых чисел ki, удовлетворяющих равенству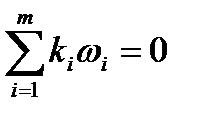 
) сколь угодно близко проходит около любой точки m -мерного тора (всюду плотна на нём). Вообще, для стационарного режима (установившегося движения системы) характерны траектории, плотные в некотором подмножестве фазового пространства, а для переходного процесса траектории, не возвращающиеся в окрестность своих начальных точек.
2.5. Уравнения движения маятника
Рассмотрим движение маятника без трения (Higham, Higham 2005 (177-179)). Уравнение движения в этом случае имеет вид:
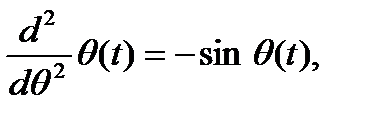
здесь θ – угол отклонения маятника от вертикали.
Определив y 1(t) = θ (t) и y 2(t) = dθ (t)/ dt, можно ОДУ 2-го порядка записать как систему из двух ОДУ первого порядка:
| ||
|
Эта система уравнений может быть запрограммирована следующей m–функцией:
function yprime=pendd(t,y)
yprime=[y(2);-sin(y(1))];
Следующий m-файл дает возможность вычислить движение маятника на временном интервале 0 < t < 8 для трех различных начальных условий yazero=[1;1], ybzero=[-5;2], yczero=[5;-2].
Первая строка это название m-файла. Третий оператор снизу дает возможность поместить на график с помощью мыши название соответствующим графикам. Оператор xlim([-5 5]) ограничивает отображение интервала колебаний маятника.
|
|
|
%ppend
tspan=[0 8];
yazero=[1;1];
ybzero=[-5;2];
yczero=[5;-2];
[ta,ya]=ode45(@pendd,tspan,yazero);
[tb,yb]=ode45(@pendd,tspan,ybzero);
[tc,yc]=ode45(@pendd,tspan,yczero);
hold on
plot(ya(:,1),ya(:,2))
plot(yb(:,1),yb(:,2))
plot(yc(:,1),yc(:,2))
xlim([-5 5])
xlabel('угол'); ylabel('скорость');
gtext('колебание');gtext('вращение');
hold off
grid on
Результат вычислений можно видеть на рисунке 1.
Рис. 1.
Предположим, что величина сил трения, которые, в конечном счете, приводят к остановке маятника, пропорциональна скорости маятника (Hunt et al. 2008 (сс. 216-220)). Предположим также, что длина маятника равна 1 м, масса на конце маятника составляет 1 кг, а коэффициент трения примем равным 0.5. В таком случае, уравнения движения для маятника будут следующими.
| (1) |
где t представляет время в секундах, х обозначает угол отклонения маятника от вертикальной линии в радианах (то есть х = 0 – это исходное положение), y выражает угловую скорость маятника в радианах в секунду, а постоянная 9.81 – это приблизительное ускорение, вызванное действием силы тяжести, в метрах в секунду в квадрате.
На переменную g в Command Window (CW) запрограммирована система уравнений (1):
g = @(t,x)[x(2);-0.5*x(2)- 9.81*sin(x(1))];
Возьмем в качестве начального положения х (0) = 0 и начальной скоростью у (0) = 5 и введем в CW следующую последовательность операторов:
[t, xa] = ode45(g, [0:0.01:20], [0 5]);
plot(xa(:, 1), xa(:, 2))
grid on
На рис. 2 показан график х и у как функции от t на промежутке времени 0 < t <20 для этих начальных данных. (Чтобы использовать инструмент среды MATLAB для численного решения дифференциальных уравнений ode45, мы объединим х и у в один вектор х – смотрите оперативную справку для команды ode45.)
Начав в точке (0; 5), по мере увеличения t, мы следуем за кривой, в то время как она закручивается по часовой стрелке к точке (0; 0). Маятник колеблется назад и вперед, но с каждым колебанием угол отклонения становится меньше, пока маятник совсем не вернется в состояние покоя ко времени t = 20. Одновременно скорость также периодически изменяется, достигая своих наибольших значений в течение каждого колебания, когда маятник находится в середине своего колебания (угол близок к нулю), и достигает нуля, когда маятник находится в конце своего колебания.
|
|
|
Рис. 2.
Увеличим начальную скорость до 10.
[t, xa] = ode45(g, [0:0.01:20], [0 10]);
Рис. 3.
На этот раз (Рис. 3.) угол увеличивается до значения, превышающего 14 радиан, перед тем, как кривая подходит к точке примерно (12.5; 0). Если быть более точными, кривая закручивается к точке (4π; 0), потому что 4π радиан представляет то же самое положение маятника, что и 0 радиан. Маятник выполнил два полных оборота перед началом своих затухающих колебаний. Скорость сначала уменьшается, но затем повышается после того, как угол проходит через π, поскольку маятник проходит вертикальное положение и получает импульс. Импульса маятника будет достаточно только чтобы еще раз пройти через вертикальное положение в угле 3π.
|
|
|
