Теоретические сведения о нелинейных системах

Нелинейные системы при некоторых допущениях можно аппроксимировать линейными уравнениями, но есть такие типы нелинейностей, которые нельзя свести к линейному описанию.

Примеры систем с существенными нелинейностями:

- различные виды реле (с зоной нечувствительности, гистерезисом и т. д.);

- клапаны (зоны нечувствительности, насыщение);

- нелинейные деформации механических пружин;

- падение давления в сужении трубы;

- силы трения;

- аэродинамическое сопротивление;

- свойства пара;

- двигатели постоянного тока с последовательной обмоткой возбуждения (момент – функция квадрата тока роторной цепи);

- двигатели переменного тока.

Библиотека блоков VisSim, представленная в позиции Bloks меню и инструментальными панелями, содержит «том» Nonlinear – блоки нелинейных операций и создания нелинейных систем.

Рассмотрим нелинейную систему, представленную на рис. 2.1. Эта система дополнена блоком нелинейности с порогами ограничения ±10. Поведение системы довольно необычно – вначале развиваются нарастающие колебания, но затем система вдруг залипает в стабильном состоянии с отрицательным уровнем сигнала.

Р и с. 2.1. Нелинейная система

Назвать причину этого явления с первого взгляда трудно. Между тем она заключается в специфике выбора передаточных характеристик. Оба примененных звена пропускают постоянную составляющую сигнала. И если петлевое усиление системы выше 1 (что и имеет место), то нелинейная система будет иметь два устойчивых состояниями равновесия (подобно триггеру в электронике). После некоторых колебаний она и попадает в одно из таких состояний. В нем дифференциальный коэффициент передачи прямого нелинейного канала падает до 0, и это состояние оказывается стабильным.

На рис. 2.2 приведена нелинейная система, в которой использовано единственное инерционное звено, передаточная характеристика которого имеет пик на некоторой частоте и затем падает вплоть до 10 по, обе стороны от пика. В итоге функциями триггера система не обладает и может выполнять функции автогенератора стабильных по амплитуде почти синусоидальных колебаний. На это и показывают осциллограммы выходных сигналов этой системы.

Р и с. 2.2. Нелинейная система

Рассмотрим систему автоматического регулирования температуры поточного нагревателя, представленного на рис. 2.3. Водонагреватель выполнен в виде емкости, в которой на токопроводящих стержнях 2 (рис. 2.3) и проходных изоляторах 3 подвешены пластины 1. К пластинам через изоляторы подводится переменное напряжение.

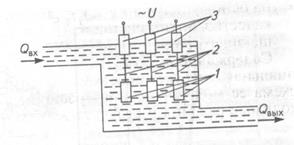
Р и с. 2.3. Поточный электродный водонагреватель

В результате протекания тока через воду она нагревается. Для стабилизации температуры воды водонагреватель оснащен бесконтактным регулятором температуры БРТ. Структурная схема САР температуры показана на рис. 2.4, где: – заданная температура; U – напряжение на электродах; – сигнал рассогласования; W(s) – передаточная функция водонагревателя; F( ) – релейная характеристика терморегулятора.

Р и с. 2.4. Структурная схема САР без учета возмущений

Передаточная функция водонагревателя по каналу регулирующего воздействия (2.1):

, (2.1)

где k –передаточный коэффициент водонагревателя, °С/В; T₁, Т₂ – постоянные времени, зависящие соответственно от массы электродов и массы воды в водонагревателе.

Значения k и T₁, Т₂ зависят от расхода (производительности) проточного водонагревателя (рис. 2.5). Релейная характеристика терморегулятора показана на рис. 2.6.

Р и с. 2.5. Зависимости параметров передаточной

функции W(s) от производительности водонагревателя

Р и с. 2.6. Релейная характеристика

терморегулятора

Структурная схема моделирования с заданными значениями параметров элементов САР представлена на рис. 2.7.

Р и с. 2.7. Модель САР

Существуют САР с элементами, статические характеристики которых описываются нелинейными аналитическими функциональными зависимостями. Такие нелинейные элементы линеаризуются на основе ряда Тейлора, в результате чего получается приближенная математическая модель системы в виде структурной схемы линеаризованной САР.

Рассмотрим ещё один пример нелинейной системы − САР температуры в инкубационной камере. Объектом регулирования в данной САР является инкубационная камера с лотком и яйцами, уложенными на нем. Регулируемая величина температура в камере _К зависит от возмущающего воздействия – температуры окружающей среды ₀. Величину _К можно регулировать, изменяя регулирующее воздействие – температуру нагревательного элемента _н.

Принципиальная схема САР температуры в камере инкубатора представлена на рис. 2.8.

Р и с. 2.8. Принципиальная схема САР температуры

в камере инкубатора

В состав данной схемы входят: 1 – инкубационная камера; 2 – термопара; 3 – лоток с яйцами; 4 – нагревательный элемент; 5 – исполнительный орган; 6 – силовой блок; 7 – блок управления тиристорами; 8 – электронный усилитель постоянного тока; 9 – задающий резистор.

Данная САР работает следующим образом. Для измерения температуры в инкубационной камере 1 имеется термопара 2, сигнал которой ЭДС Е сравнивается с задающим (опорным) сигналом U₀. Изменяя опорное напряжение U₀ с помощью резистора 9, подключенного к стабилизированному источнику постоянного тока, задают необходимую температуру в камере инкубатора ( = 37,5 ± 0,2 °С).

При этом входные и выходные величины элементов САР () будут иметь определенные значения, соответствующие заданному значению температуры в инкубаторе. Задача построения математической модели данной САР состоит в определении уравнений, отображающих взаимосвязи в объекте регулирования регулируемой величины _К с входными воздействиями _н и ₀, а в остальных элементах системы соответственно выходных величин с входными в динамическом режиме.

Передаточные функции объекта регулирования (регулирующего и воспринимающего органа) определяют на основе уравнения теплового баланса. С учетом зависимости , отображающей обратную связь в системе, математическая модель САР температуры в инкубаторе может быть представлена следующей системой уравнений:

(2.2)

Анализ данной системы уравнений показывает, что рассматриваемая САР нелинейная. Ее нелинейность обусловлена наличием нелинейного алгебраического уравнения, описывающего зависимость мощности нагревательного элемента от приложенного к нему напряжения .

С целью реализации данной нелинейности можно воспользоваться блоками, реализующими математическую обработку или воспользоваться интеграцией VisSim с матричной системой MATLAB.

Система визуального блочного математического моделирования VisSim, обеспечивает интеграцию с системой компьютерной математики MATLAB. В позиции Blocks существует отдел библиотеки блоков MATLAB Interface. Этот отдел содержит четыре блока.

MATLAB Expression – задание выражения, записанного на языке системы MATLAB.

MATLAB Read Variable – импорт значения MATLAB переменной.

MATLAB Write Variable – экспорт в MATLAB переменной.

About VisSim/ MATLAB Interfase – вывод окна с информацией о версии интерфейса связи систем VisSim и MATLAB.

Рассмотрим пример связи системы VisSim и MATLAB. Имея созданную переменную в рабочем пространстве VisSim, произведем вычисления с этой переменной в системе MATLAB, затем снова проведем считывание новой переменной из пространства VisSim. В приведенном на рис. 2.9 примере массив – матрица [1 2; 3 4] – присваивается переменной Xmatlab системы MATLAB. Для этого надо ввести этот массив как константу VisSim, а затем ввести блок MatLab Write Variable. В окне его свойств нужно задать имя переменной – Xmatlab, после чего оно и появится в графическом изображении блока, заменив первоначальное имя блока. При исполнении этого примера в рабочем пространстве системы MATLAB будет создана данная переменная с заданным значением. В MATLAB над ней можно будет проделывать любые численные операции, например, вычислить детерминант матрицы, осуществить ее транспозицию и инвертирование и т. д.

Этот пример иллюстрирует также считывание переменной Xmatlab из рабочего пространства памяти системы MATLAB. Для этого используется блок MatLab Read Variable, в окне которого надо задать имя переменной – Xmatlab (рис. 2.10). Считанное значение индицируется цифровым индикатором системы VisSim. Вы можете задать запуск создания MATLAB переменной или ее считывание только при первом запуске VisSim, точнее, при первом шаге моделирования. Соответствующая опция есть в левом нижнем углу окон свойств переменных.

Р и с. 2.9. Задание и считывание переменной MATLAB

Р и с. 2.10. Окно свойств переменной Xmatlab

Все это будет иметь место после пуска моделирования и загрузки системы MATLAB. Однако нетрудно убедиться в том, что переменная матричного типа Xmatlab действительно создана в рабочем пространстве памяти системы MATLAB. Для этого достаточно исполнить в окне MATLAB команду

>> Xmatlab

Тут же будет выведен следующий результат:

Xmatlab =

1 2

3 4

Можно также создавать в окне MATLAB новые переменные и вообще использовать любые доступные в этой системе команды.

Для рассматриваемой САР температуры в инкубаторе, передаточные функции будут иметь вид:

W = = 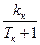– передаточная функция камеры инкубатора по регулирующему воздействию;

W = = – передаточная функция камеры инкубатора по возмущающему воздействию;

W = = – передаточная функция термопары;

W 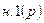= = – передаточная функция нагревателя по каналу мощности P;

W = = – передаточная функция нагревателя по каналу температуры _К;

W = = 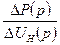– передаточная функция, соответствующая линеаризованному уравнению ;

W 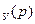= = 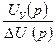– передаточная функция электронного усилителя;

W = = – передаточная функция теристорного регулятора напряжения.

Схема нелинейной САР представлена на рис. 2.11.

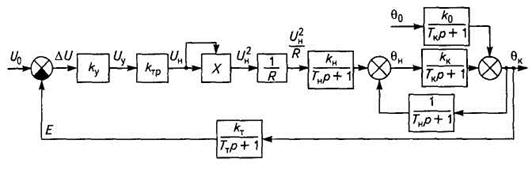
Р и с. 2.11. Структурная схема нелинейной САР

температуры в инкубаторе

Задание на выполнение лабораторной работы

Задание 1

Необходимо смоделировать работу проточного нагревателя. В процессе моделирования САР проточного нагревателя определите зависимости параметров автоколебаний (амплитуды A и частоты автоколебаний) варьируемого параметра релейного регулятора – зоны нечувствительности регулятора. По результатам моделирования постройте графики зависимостей А = f( ) и = f () и на их основе определите рациональное значение зоны нечувствительности для исследуемой системы, исходя из показателей ее надежности и требований технологического процесса, которые должны обеспечиваться соответствующими показателями качества САР. Одно из технологических требований – точность стабилизации регулируемой величины. Для автоматической системы стабилизации температуры воды на выходе водонагревателя допускаются отклонения температуры от заданного значения в пределах ±10%. Варианты заданий, составленные с учетом графических зависимостей (см. рис. 2.5), приведены в табл. 2.1.

Таблица 2.1