 |
Теоретические сведения о структурах управления
|
|
|
|
При неизменных свойствах объекта качество регулирования в АСР зависит от свойств остальных её элементов, в первую очередь регулятора. Свойства регулятора определяются характером преобразования его входного сигнала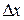 
в выходной z.
Несмотря на большое разнообразие объектов регулирования, характерные их свойства, имеющие существенное значение для целей управления, немногочисленны, как и сами способы управления объектами. Для создания систем управления могут использоваться блоки стандартной библиотеки блоков VisSim. В дополнительных библиотеках и примерах применения системы VisSim существует набор специальных блоков (C:\VisSim45\Toolbox\Controls). Рассмотрим некоторые специальные блоки.
Блок пропорционального регулятора. Для создания систем с обратной связью приходится использовать структуру пропорционального регулятора, представленную на рис. 3.1.
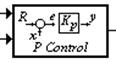
Р и с. 3.1. Блок П-регулятора
Данный блок содержит суммирующе-вычитающее устройство с двумя входами и умножитель. Коэффициент передачи устройства задается параметром Proportional Gain, значение которого задано равным 1, но может меняться. На рис. 3.2 представлена диаграмма пропорционального регулятора.
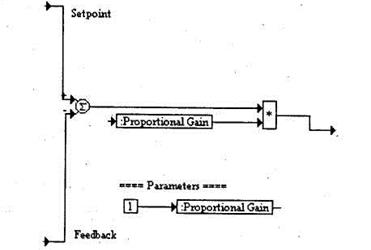
Р и с. 3.2. Диаграмма пропорционального
регулятора
Организация линейной системы с помощью этого блока представлена на рис. 3.3.
Р и с. 3.3. Структурная схема САР
с использованием П-регулятора
Кроме блока Proportional Gain используется блок задания передаточной функции, что позволяет учесть инерционность системы.
Блок ПИ-регулятора. Многие системы строятся с регуляторами, в которых, помимо пропорционального звена, включается интегрирующее звено. Такие регуляторы принято называть пропорционально-интегрирующимиили регуляторами ПИ (PI) типа. Блок ПИ-регулятора представлен на рис. 3.4.
|
|
|
Р и с. 3.4. Блок ПИ-регулятора
Структурная схема блока PI Control такого типа представлена на рис. 3.5.
Р и с. 3.5. Структурная схема блока ПИ-регулятора
Блок ПИД-регулятора. В задачах управления объектами часто используются пропорционально-интегро-дифференциальные регуляторы ПИД (PID). Такие регуляторы реализует блок PID Control, представленный на рис. 3.6.
Р и с. 3.6. Блок ПИД-регулятора
Применение блока PID Control заметно упрощает построение систем на базе ПИД-регуляторов. Структурная схема блока PID Control представлена на рис. 3.7.
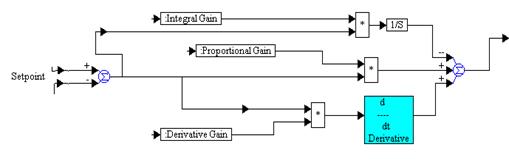
Р и с. 3.7. Структурная схема блока PID Control
Оптимизация завершенной модели является целью многих задач моделирования. В VisSim она реализуется особым построением модели, в которую включаются специальные блоки для многократного моделирования с изменяющимися параметрами. Оптимизация модели заключается в подборе её параметров, при котором обеспечивается минимум некоторой целевой функции.
Установку общих параметров оптимизации можно выполнить из окна установок оптимизации, которое выводится командой Optimization properties … в позиции Simulation меню. В этом окне можно выбрать метод оптимизации:
Powel – безградиентный метод Поувелла, в котором вычисления производных выполняются по упрощенным разностным формулам, что обеспечивает повышенную скорость оптимизации;
Polak-Rabiere – градиентный метод Полака-Райбера, оптимизированный под поиск минимума функций, близкий к квадратичным зависимостям в окрестности точки минимума;
Fletcher-Reeves – градиентный метод Флетчера-Ривеса, имеющий лучшую сходимость, чем метод Полака-Райбера, но несколько меньшую скорость поиска;
User Method – оптимизация методом пользователя.
Для включения оптимизации надо задать опцию Perform Optimization. В окне установок параметров оптимизации можно также задать максимальное количество итераций Max Iterations и допуск ошибки.
|
|
|
Error Tolerance (разность значений целевой функции для двух последних итераций). По умолчанию эти параметры равны 50 и 1 соответственно. Задание большего Error Tolerance позволяет уменьшить число итераций и полезно в случаях, когда оптимизаторы «зацикливаются».
Рассмотрим блоки оптимизации. Блок задаваемых ограничений constraint служит для задания при оптимизации необходимых ограничений. Он используется решателями, задающими решение итерационными методами уравнений без использования производных. Блок используется в паре с блоком unknown.
Блок cost служит для задания целевой функции. Он используется оптимизаторами системы VisSim, обеспечивающими автоматический подбор параметров системы в итерационном процессе. Блок используется в паре с блоком parameterUnknown.
Блок globalConstraint предназначен для создания связи с собственным оптимизатором пользователя, написанным на языке С ++, Паскаль и др.
Блок parameterUnknown используется оптимизаторами для подстановки в блок схем, подбираемых ими в итерационном процессе повторного моделирования со значениями параметров системы, минимизирующими целевую функцию. Блок используется в паре с блоком-датчиком целевой функции.
Блок unknown используется неявными решателями для подстановки в блок-схему начальных значений неизвестных величин. Цель применения пары блоков unknown и constraint – решение уравнений, которые не содержат производные.
Рассмотрим пример оптимизации системы с ПИД-регулятором (рис. 3.8). Модель представляет собой типичную линейную замкнутую систему, имеющую заданную блоком Plant передаточную характеристику и ПИД-регулятор в цепи обратной связи. Назначение модели – создание системы, переходная характеристика которой должна быть монотонной и обеспечивать минимальное время нарастания.
Решается задача оптимизации коэффициентов, которые в модели обозначены P, I, D. Критерием оптимизации является получение минимального времени установления переходного процесса при заданном выбросе на вершине в 10%. Процесс начинается при значениях P, I, D, равных 1, а заканчивается при оптимальных значениях этих коэффициентов.
Р и с. 3.8. Модель системы с ПИД-регулятором
|
|
|
Субмодель ObjectiveFunction (рис. 3.9) служит для задания целевой функции и блок cost для оптимизации. Благодаря средствам оптимизации данная модель обеспечивает неоднократное вычисление переходной характеристики данной замкнутой системы и выводит графики ошибки и графики вычисленных переходных характеристик.
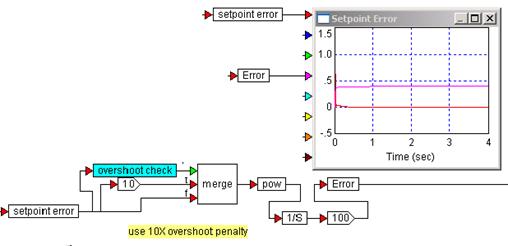
Р и с. 3.9. Субмодель ObjectiveFunction
Диаграмма субмодели Meassuement показана на рис. 3.10. С помощью субблока Plant (рис. 3.11) задается вполне определенная передаточная характеристика. Реализованное в блоке задание передаточной характеристики является альтернативным вариантом применения блока Тransfer Function. На рис. 3.12 показан график переходного процесса системы на момент окончания оптимизации. Демонстрационный пример оптимизации модели находится VisSim/Appexmpl/Optimize/Pidtunez.
Р и с. 3.10. Диаграмма блока измерений Meassuement
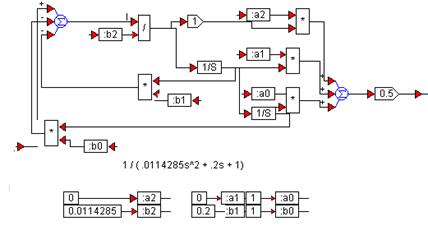
Р и с. 3.11. Диаграмма субмодели Plant
Р и с. 3.12. График переходного процесса
Задание на выполнение лабораторной работы
Задание 1
Одна из основных стадий производства экстракционной фосфорной кислоты (ЭФК.) – сернокислотное разложение фосфатного сырья в реакторе с мешалкой. Стабилизация заданной концентрации ионов SO 
в жидкой фазе пульпы в реакторе должна обеспечить наилучшие условия разложения фосфатного сырья и кристаллизацию сульфата кальция. На рис. 3.13 представлена схема реактора.
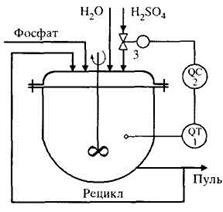
Р и с. 3.13. Схема реактора
разложения фосфатного сырья
Исследования реактора как объекта автоматического управления показали, что передаточная функция, связывающая концентрацию SO в зоне реакции с расходом H2SO4 с достаточной для практики точностью может быть представлена в следующем виде (3.1):
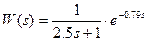. (3.1)
А. Регулирование концентрации ионов SO в реакторе с мешалкой осуществляется с помощью расхода H2SO4. В систему регулирования, кроме реактора, входят также измерительный прибор (автоматический анализатор, построенный на базе кондуктометра), регулятор 2, формирующий пропорциональный закон регулирования и исполнительный механизм с регулирующим клапаном 3. Их передаточные функции заданы в таком виде (3.2), (3.3), (3.4):
|
|
|
; (3.2)
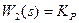; (3.3)
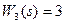. (3.4)
Определите коэффициент усиления Кр регулятора для условий регулирования с 50% запасом устойчивости по амплитуде.
Б. Для улучшения качества регулирования вместо П-регулятора установили ПИ-регулятор (3.5):
. (3.5)
Для нескольких значений времени изодрома 
определите коэффициент усиления регулятора, обеспечивающий запас устойчивости по амплитуде 50% запасом устойчивости по амплитуде.
В. Решите задачу оптимизации коэффициентов регуляторов.
Задание 2
Функциональная схема регулирования концентрации в реакторе приведена на рис. 3.14.
Р и с. 3.14. Система регулирования концентрации
В реакторе идеального смешения происходит непрерывная каталитическая реакция. Концентрация продукта на выходе из реактора регулируется изменением расхода катализатора F, что приводит к изменению его концентрации в реакторе 
(3.6):
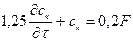. (3.6)
При этом концентрация продукта в выходящем из реактора потоке с, зависящая от концентрации катализатора тоже будет изменяться: (постоянные времени даны в минутах) (3.7):
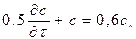. (3.7)
Кроме реактора в систему регулирования также входят:
1. Измерительное устройство 1, состоящее из безынерционного измерительного прибора с коэффициентом усиления 
и системы отбора проб, создающей транспортное запаздывание 
= 0,3 мин.
2. Регулятор 2.
3. Исполнительное устройство 3 (исполнительный механизм с регулирующим клапаном), по динамическим свойствам аналогичное статическому звену нулевого порядка с коэффициентами усиления К3 = 5.
А. Как будет меняться концентрация катализатора в реакторе ск(
), если в условиях, когда система находилась в статическом режиме, а регулятор был отключен, произошло ступенчатое изменение расхода катализатора F от 20 кг/мин до 24 кг/мин?
Б. Определите, будет ли система регулирования устойчива, если регулятор реализует:
ПИ-закон регулирования (Кр = 2; T 
= 0,2);
ПИД-закон регулирования (Кр = 2; Т = 0,2; Т 
= 1).
В. Решите задачу оптимизации коэффициентов регуляторов.
Порядок выполнения работы
1. Ознакомиться со всеми пунктами методических указаний.
2. Получить у преподавателя вариант задания на выполнение лабораторной работы.
3. Составить функциональную схему САР исследуемой системы.
4. Заполнить схемное окно пакета VisSim необходимыми типовыми блоками.
5. Придайте используемым блокам нужную ориентацию и осуществите соединение блоков.
6. Согласно вашему варианту задания введите необходимые параметры структурной схемы, используя диалоговые окна.
7. Установите параметры моделирования.
8. Запустите модель и проанализируйте полученные результаты.
|
|
|
9. Покажите преподавателю результаты работы.
Содержание отчета
1. Номер, название и цель работы.
2. Задание на выполнение лабораторной работы (функциональная схема САР, структурная схема САР, параметры передаточных функций САР).
3. Модель САР.
4. Результаты, полученные в процессе моделирования.
5. Выводы по выполненной работе.
6. Ответы на контрольные вопросы.
Контрольные вопросы
1. Дайте определение процессу оптимизации системы?
2. Каков принцип работы САР концентрации в реакторе?
3. Перечислите способы регулирования расхода.
4. Как реализуется дифференцирующее звено в системе VisSim?
5. Какие специальные блоки оптимизации существуют в системе VisSim?
6. Назовите методы оптимизации, в чем их отличие?
Лабораторная работа № 4
МОДЕЛИРОВАНИЕ СОБЫТИЙНО-УПРАВЛЯЕМЫХ СИСТЕМ В ПАКЕТЕ STATEFLOW СИСТЕМЫ MATLAB
Цель работы: овладеть навыками работы с инструментом проектирования событийно-управляемых систем, характеризующихся сложным поведением.
|
|
|
