 |
В пакете Fuzzy Logic Toolbox
|
|
|
|
Гибридная сеть – это многослойная нейронная сеть специальной структуры без обратных связей, в которой используются обычные (не нечеткие) сигналы, веса и функции активации, а выполнение операции суммирования основано на применение фиксированной Т-формы, или некоторой другой непрерывной операции. При этом значения входов, выходов и весов гибридной нейронной сети представляют собой вещественные числа из отрезка [0, 1].
В основе модели гибридных сетей лежит идея о возможности использования существующей выборки данных для определения параметров функции принадлежности, которые наилучшим образом соответствуют проектируемой системе нечеткого вывода. При этом для нахождения параметров функции принадлежности используются известные процедуры обучения нейронных сетей.
В пакете Fuzzy Logic Toolbox гибридные сети реализованы в форме так называемой адаптивной системы нейронечеткого вывода ANFIS. Гибридная сеть ANFIS представляет собой нейронную сеть с единственным выходом и несколькими входами, которые представляют собой нечеткие ЛП. Термы входных ЛП описываются стандартными для системы MATLAB функциями принадлежности, а термы выходной переменной представляются линейной или постоянной функциями принадлежности.
Кроме того, гибридная сеть ANFIS представляет собой систему нечеткого вывода FIS типа Сугено 0-го или 1-го порядка, в которой каждое правило нечетких продукций имеет постоянный вес, равный единице. Гибридные сети ANFIS можно настраивать и редактировать аналогично системам нечеткого вывода FIS, используя все средства пакета Fuzzy Logic Toolbox. В пакете Fuzzy Logic Toolbox гибридные сети реализованы в форме адаптивных систем нейронечеткого вывода ANFIS. При этом разработка и исследование гибридных сетей может осуществляться: в интерактивном режиме с помощью специального графического редактора адаптивных сетей – редактора ANFIS; в режиме командной строки с помощью ввода имен соответствующих функций непосредственно в окно команд системы MATLAB.
|
|
|
Редактор ANFIS позволяет создавать или загружать конкретную модель адаптивной системы нейронечеткого вывода, выполнять ее обучение, визуализировать ее структуру, изменять и настраивать ее параметры, использовать настроенную сеть для получения результатов нечеткого вывода. Графический интерфейс ANFIS вызывается функцией anfisedit в режиме командной строки (рис. 5.1).
Главное меню редактора ANFIS предназначено для работы с предварительно созданной системой нечеткого вывода. Основную часть графического интерфейса занимает окно визуализации данных, расположенное ниже главного меню. Это окно не содержит никаких данных для вновь создаваемой гибридной сети.
Для создания гибридной сети необходимо загрузить данные. Для этого предназначена кнопка Load Data в левой нижней части графического окна. При этом данные могут быть загружены:
- из внешнего файла (disk);
- из рабочей области (worksp.).

Р и с. 5.1. Графический интерфейс редактора ANFIS
В данной лабораторной работе предлагается использовать нечеткие алгоритмы управления для САР. При создании САР звено регулятора заменяется блоком нечетких высказываний. Рассмотрим в качестве примера САУ, представленную на рис. 5.2.

Р и с. 5.2. Структурная схема САУ
При создании адаптивной системы нейронечеткого вывода необходимо иметь исходные данные, в виде числовых матриц, необходимые для обучения.
Для сохранения данных в виде матриц соответствующего формата можно использовать блоки сохранения То File и То Workspace (рис. 5.3). Блоки получателей информации содержит библиотека Sinks. На каждом такте моделирования формируется колонка, содержащая время такта и входные данные. Блок То File записывает полученную матрицу в файл с указанным именем.
|
|
|

Р и с. 5.3. Окно параметров блока То File
В этом окне задается имя файла, максимальное число строк, разрядность в десятичных долях времени в тактах эталонное время (чтобы зафиксировать состояние системы при t=0, это время по умолчанию задается равным -1). Блок То Workspace записывает указанную матрицу (но без строки отсчетов времени) в рабочее пространство.
Полученные данные можно просматривать и редактировать с помощью графического интерфейса редактора Array Editor (рис. 5.4). Здесь помимо уже описанных параметров задается формат записи: структура Structure, структура со временем Structure with time и массив Array.
При загрузке данных, необходимых для обучения, из внешнего файла, необходимо предварительно создать файл с исходными данными – файл с расширением .dat.
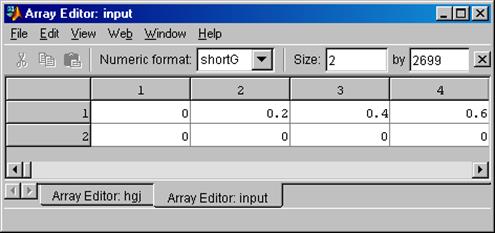
Р и с. 5.4. Графический интерфейс редактора Array Editor
Исходные данные представляют собой обычную числовую матрицу размерности т(п+1), в которой количество строк т соответствует объему выборки, первые п столбцов – значениям входных переменных модели, а последний столбец – значению выходной переменной. При этом отдельные значения матрицы отделяются друг от друга пробелами, а каждая строка матрицы завершается «переводом каретки» (клавиша Enter ) (рис. 5.5).
Принято считать, что качество обучения гибридной сети и точность получаемых результатов пропорционально зависят от объема обучающей выборки, т. е. чем больше количество строк матрицы исходных данных, тем лучше.
Загружаемые данные могут иметь следующий тип:
- обучающие данные (Training) – обязательные данные, используемые для построения гибридной сети;
- тестовые данные (Testing) – данные, применяемые для тестирования построенной гибридной сети с целью проверки качества функционирования построенной гибридной сети;
- проверочные данные (Checking) – данные, используемые для проверки построенной гибридной сети с целью выяснения факта переобучения гибридной сети;
- демонстрационные данные (Demo) – позволяют загрузить один из демонстрационных примеров гибридной сети.
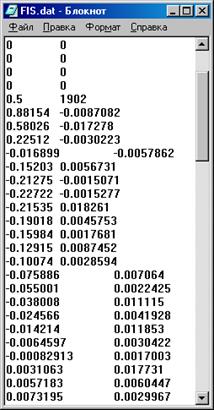
Р и с. 5.5. Обучающие данные для демонстрации
|
|
|
возможностей обучения гибридной сети ANFIS
Для редактирования данных может быть использован любой текстовый редактор. После загрузки обучающих данных, в рабочем окне редактора ANFIS будет отражена их структура (рис. 5.6.).

Р и с. 5.6. Графический интерфейс редактораANFIS
после загрузки файла с обучающими данными
Исходный график можно дополнить проверочными данными.
После подготовки и загрузки обучающих данных можно сгенерировать структуру нечеткого вывода типа Сугено, нажав кнопку Generate FIS в нижней части рабочего окна редактора. При этом две первые опции относятся к предварительно созданной структуре гибридной сети, а две последние – к форме разбиения входных переменных модели.
Структура уже созданной ранее FIS может быть загружена:
- с диска (Load from disk);
- из рабочей области (Load from worksp.).
При нажатии на кнопку Generate FIS вызывается диалоговое окно с указанием числа и типа функций принадлежности (ФП) для отдельных термов входных переменных и выходной переменной (рис. 5.7).

Р и с. 5.7. Диалоговое окно для задания количества
и типа функций принадлежности
При этом можно выбрать любой тип ФП из реализованных в системе MATLAB. После генерации структуры гибридной сети можно вывести на экран ее структуру, нажав кнопку Structure в правой части графического окна. Структура сгенерированной системы нечеткого вывода выводится в новом диалоговом окне и тривиальна по своему виду (рис. 5.8).
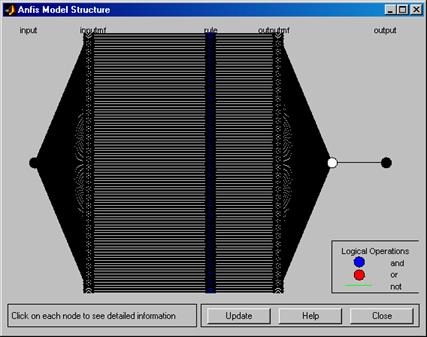
Р и с. 5.8. Структура сгенерированной системы нечеткого вывода
с одной входной переменной с 250 термами, 250 правилами
Перед обучением гибридной сети следует, используя группу опций в правой нижней части рабочего окна, задать параметры обучения:
- выбрать метод обучения гибридной сети – обратного распространения (backpropa) или гибридный (hybrid), представляющий собой комбинацию метода наименьших квадратов и метода убывания обратного градиента;
- установить уровень ошибки обучения (Error Tolerance) – по умолчанию равен нулю (изменять его не рекомендуется);
- задать количество циклов обучения (Epochs).
|
|
|
Для обучения сети следует нажать кнопку Train Now. При этом процесс обучения отображается в окне визуализации в виде графика зависимости ошибки обучения от циклов обучения (рис. 5.9). Дальнейшая настройка параметров построенной и обученной гибридной сети может быть выполнена с помощью стандартных средств пакета Fuzzy Logic Toolbox.

Р и с. 5.9. График зависимости ошибки обучения
от количества циклов обучения системы
Функция Fuzblock вызывает систему Simulink, в которой содержатся три специальных блока (рис. 5.10):
- контроллер нечеткой логики (Fuzzy Logic Controller);
- контроллер нечеткой логики с окном просмотра правил (Fuzzy Logic Controller with Rule Viewer);
- блок функций принадлежности MF.
При этом созданная FIS должна быть сохранена во внеш-нем файле с расширением .fis, а затем загружена в редактор систем нечеткого вывода FIS (рис. 5.11). Вызов графических средств FIS возможен непосредст-венно из главного меню редактора ANFIS.

Р и с. 5.10. Графический интерфейс блоков
нечеткой логики системы Simulink

Р и с. 5.11. Графический интерфейс редактора FIS
для системы нечеткого вывода
После всех выполненных операций рабочее пространство системы MATLAB содержит входные, выходные данные и модель FIS (АС2) (рис. 5.12).

Р и с. 5.12. Браузер просмотра ресурсов
рабочей области Workspace
После того как система нечеткого вывода создана, дополним структурную схему САР блоком Fuzzy Logic Controller, исключив из схемы регулятор и блоки получателей информации То File.
Результирующая структурная схема САР будет иметь вид, представленный на рис. 5.13, после чего можно осуществить запуск модели.

Р и с. 5.13. Структурная схема системы
нечеткого регулирования в среде Simulink
Результаты моделирования (рис. 5.14) показывают, что нечеткая САР не уступает по качеству регулирования САР, реализуемой известным способом. К преимуществам нечеткого регулирования систем следует отнести, что при наличии современных систем программирования ПЛК со встроенными библиотеками нечеткого управления, имеющих хороший графический интерфейс, очень легко и наглядно представляется и корректируется вид функций принадлежности и НВ. Следовательно, упрощается построение и на-стройка САР.

Р и с. 5.14. График переходного процесса нечеткой САР
Порядок выполнения работы
1. Ознакомиться со всеми пунктами методических указаний.
2. Получить у преподавателя задание на выполнение лабораторной работы.
3. Создать модель САР используя Simulink.
4. Снять необходимые для создания гибридной сети данные, используя блоки to File.
5. Создать файл с обучающимися данными – файл с расширением.dat.
6. Загрузить обучающие данные в окно редактора ANFIS.
|
|
|
7. Загрузить проверочные данные в редактор ANFIS.
8. Задать количество и тип функций принадлежности с необходимым количеством терм. Исследовать несколько вариантов системы нечеткого вывода для рассматриваемого примера: одна входная переменная с 10 термами, 10 правил нечетких продукций, одна выходная переменная с 10 термами; одна входная переменная с 50 термами, 50 правил нечетких продукций, одна выходная переменная с 50 термами; одна входная переменная с 200 термами, 200 правил нечетких продукций, одна выходная переменная с 200 термами.
9. Сгенерировать структуру нечеткого вывода.
10. Выполнить дополнительные этапы тестирования для проверки гибридной сети.
11. Проанализировать графики зависимости ошибки обучения от количества циклов обучения.
12. Сохранить созданную модель во внешнем файле с расширением.fis, а затем загрузить в редактор системы нечеткого вывода FIS.
13. Запустить модель и проанализировать полученные результаты.
Содержание отчета
1. Номер, название и цель работы.
2. Задание на выполнение лабораторной работы (функциональная схема САР, структурная схема САР, параметры передаточных функций САР).
3. Модель САР.
4. Результаты, полученные в процессе моделирования, сохраненные во внешнем файле с расширением .fis.
5. Выводы по выполненной работе.
6. Ответы на контрольные вопросы.
Контрольные вопросы
1. Дайте определение термину «нейронная сеть».
2. Что входит в состав структуры искусственного нейрона?
3. В чем отличие нейронной сети прямого распространения от рекуррентной сети?
4. Назовите графические средства, входящие в состав пакета Fuzzy Logic Toolbox используемые для разработки систем нечеткого вывода?
5. Дайте определение многослойной нейронной сети.
6. Назовите методы обучения гибридной сети.
7. Каким образом происходит обучение нейронной сети в MATLAB?
8. Чему равен уровень обучения, установленный по умолчанию?
Лабораторная работа № 6
ИСПОЛЬЗОВАНИЕ АЛГОРИТМОВ НЕЧЕТКОГО ВЫВОДА ПРИ МОДЕЛИРОВАНИИ СИСТЕМ В СРЕДЕ MATLAB
Цель работы:
ü изучить метод построения нечёткой системы средствами инструментария Fuzzy Logic в системе MATLAB.
ü освоить методы построения нечётких множеств с иcпользованием различных типов функций принадлежности и ознакомиться с наиболее распространенными логическими операциями над нечёткими множествами.
|
|
|


