 |
Сохранить статистический анализ подгонки моделей.
|
|
|
|
Процедура 1. Проведение анализа подгонки моделей, расчет критерия согласия χ2
Вызов анализа осуществляется командой – Describe ® Numeric Data ® Distribution Fitting (Описание ® Числовые данные ® Подгонка моделей) (Рис. 42)
. 
Рис. 42. Процедура вызова анализа подгонки модели
На экране появляется окно ввода вектора данных с одноименным названием Distribution Fitting. В поле с именем [Data:] (Данные) введите имя вектора данных, по которому необходимо провести анализ (Рис.43).


Рис.43. Ввод переменной в анализ Подгонки модели
После нажатия клавиши [OK] появляется первое окно анализа подгонки моделей – [Analysis Summary] (Рис.44). Оно говорит по какой переменной проводится анализ – [Data variable:]. Далее программа рассчитывает параметры распределения. По умолчанию видно, что расчет идет для нормального распределения [normal distribution:], оно является двухпараметрическим. Вычислены параметры нормального распределения:
[mean] – среднее,
[standart deviation] – стандартное (среднеквадратическое) отклонение.


Рис.44. Окно Analysis Summary
Для определения согласия между эмпирическим рядом распределения и теоретической моделью необходимо рассчитать критерий согласия χ2. Для этого нажмите кнопку на панели инструментов [Tabular Options] анализа подгонки моделей (Рис.44). Появится диалоговое окно (Рис.45), где необходимо отметить, кроме пункта меню (Analysis Summary), пункт (Goodness of-Fit Tests) (Тесты на согласие модели). После этого нажмите клавишу [OK].

Рис. 45. Выбор расчета критерия согласия
В появившемся окне (Рис.46) проведите коррекцию количества классов, нижнего и верхнего действительных значений классов в полях ввода (см. пояснения к рис. 23). После корректировки параметров таблицы частотной табуляции, таблица расчета критерия согласия χ2 имеет вид (Рис.47).
|
|
|
|
|


Рис. 46. Окно расчета критерия согласия χ2


Рис. 47. Окно расчета критериев согласия для нормального распределения после корректировки параметров частотной табуляции
Основное место на рис.47 занимает таблица расчета критерия согласия χ2 [Chi-Square Test]. В таблице пять столбцов:
1-й – нижние действительные значения разрядов;
2-й – верхние действительные значения разрядов;
3-й – эмпирические частоты по разрядам (ni);
4-й – теоретические частоты по разрядам ( );
);
5-й –критерий согласия χ2выч по разрядам.
Под таблицей рассчитано χ2 выч =3,03; число степеней свободы df =4, уровень значимости p-Value =0,55.
Процедура 2. Графическое изображение результатов подгонки моделей
Для получения графика результатов анализа нажмите клавишу [Graphical Options] на панели инструментов (см. рис. 44), в появившемся окне отметьте пункт [Frequency Histogram] (Рис. 48).

Рис. 48. Вызов операции подгонки распределений
На экране появится гистограмма эмпирического ряда распределения по исследуемому признаку и теоретическая кривая модельного распределения (Рис.49).
|
|


Рис. 49. График отображения теоретической модели нормального распределения на гистограмме ряда распределения
По результатам проведенного анализа заполняется табл. 1, для этого выпишите для исследуемого вектора данных значения χ 2выч и число степеней свободы df по подгоняемому теоретическому распределению (Рис.47) (по умолчанию система Statgraphics Plus производит подгонку по модели нормального распределения (Normal)).
Для смены теоретического распределения в окне расчета критерия согласия χ2 (Рис.47) вызовите контекстное меню. Выберите в нем команду (Analysis Options). Появится окно диалога (Distribution Fitting Options) (Рис. 50).
|
|
|
Программа Statgraphics Plus позволяет рассчитывать подгонку по 5 теоретическим моделям распределений. Все они могут быть применены для непрерывных данных. После выбора модели нажмите клавишу [OK], система выведет на экран рассчитанные параметры выбранного модельного распределения (Рис.51).
Таблица 1
Сводная таблица результатов анализа подгонки моделей теоретических распределений
| Вид распределения | D, см | H, м | V, м3 | |||
| значение χ2 | число степеней свободы df | значе-ние χ2 | число степеней свободы df | значе-ние χ2 | число степеней свободы df | |
| нормальное (Normal) | 3,029 | |||||
| логарифмически нормальное (Lognormal) | 6,020 | |||||
| Вейбулла (Weibull) | 3,412 | |||||
| экспоненциальное (Exponentional) | 144,076 |
Рис. 50. Переход к другой модели
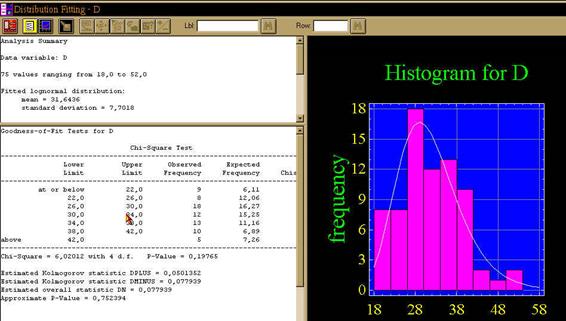
Рис. 51. Результаты подгонки логарифмически-нормального распределения
Необходимо выбрать закон распределения, который наилучшим образом описывает эмпирические данные, для этого используем таблицу значений χ2 при различных уровнях значимости (Прил.1).
|
|
|


