 |
Циркуляция тепла в одномерном потоке теплопроводного газа как причина генерации энергии и основа возникновения самоподдерживающегося течения.
|
|
|
|
Циркуляция тепла в одномерном потоке теплопроводного газа как причина генерации энергии и основа возникновения самоподдерживающегося течения.
Далее мы покажем, что внутренняя циркуляция тепла в прямолинейном течении может вызвать генерацию механической энергии. В первую очередь, следует подчеркнуть, что при энергоизолированном течении теплопроводного газа можно наблюдать странный процесс падения температуры, который существенно отличается от процесса адиабатного ускорения (дросселирования) тем, что процесс падения температуры одновременно сопровождается падением энтропии -. иными словами, мы покажем, что в теплопроводной системе на самом деле можно осуществить процесс имплозии, который на рис. 4, б выражается линией a-b. В T-s координатах такой процесс протекает подобно процессу с охлаждением извне.
Рис. 5. Ускорение теплопроводного газа
Рассмотрим процесс ускорения газа, который характеризуется высоким коэффициентом теплопроводности. Как известно, для анализа процессов в энергоизолированном потоке газа применяется условие сохранения энергии в виде:
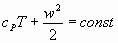(4)
Отсюда следует, что при увеличении скорости вдоль течения температура потока будет уменьшаться. Следовательно, если температура падает, то согласно закону Фурье должен возникнуть тепловой поток, который будет направлен также вдоль течения (по течению):
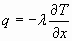(5)
Несмотря на то, что теплопроводность газов невелика, если мы хотим найти такой процесс охлаждения, при котором падение температуры сопровождается снижением энтропии, то нужно рассмотреть процесс теплопроводности. Для этого необходимо рассмотреть такое ускорение газа, в котором при падении температуры вдоль течения возникает нарастающий поток тепла, при этом внутреннее перераспределение тепла не будет нарушать условие баланса энергии - общий поток энергии в любом сечении будет оставаться одинаковым:
|
|
|
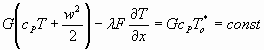( 6)
Последний член в данном уравнении отражает суммарный тепловой поток, который проходит через произвольное сечение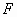 
. Изменение энтропии из-за перераспределения тепла зависит от характера изменения теплового потока вдоль течения:
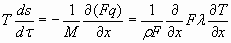, ( 7 )
Или
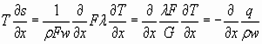. (8)
Если последнее уравнение проинтегрировать в пределах от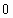 
до 
(где - координата рассматриваемого сечения), то получим:
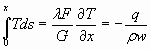(9)
Таким образом, если в произвольном сечении тепловой поток направлен в сторону потока массы, то процесс характеризуется уменьшением энтропии на рассматриваемом участке, а уравнение энергии (6) примет вид:
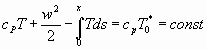. (10)
Следовательно, если в каком-то резервуаре находится теплопроводный газ с температурой окружающей среды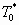 
, то процесс истечения газа из такого резервуара на участке ускорения потока будет характеризоваться не только падением температуры, но и снижением энтропии (рис. 6):
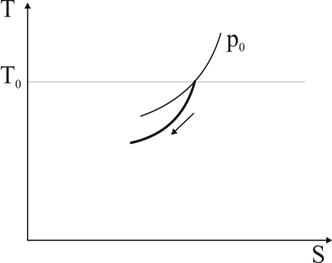
Рис. 6. Истечение теплопроводного газа как пример одновременного снижения энтропии и охлаждения ниже температуры окружающей среды – имплозия.
Таким образом, при ускорении теплопроводного газа налицо процесс падения температуры ниже 
одновременно со снижением энтропии без передачи тепла окружающему пространству. А это значит, что аккумулированная в потоке тепла q тепловая энергияможет вновь возвращаться потоку массы М без потерь в процессе торможения - учитывая, что рассмотренный процесс похож на процесс охлаждения извне, можно сказать, что имеет место кажущийся эффект охлаждения. Иными словами, течение теплопроводного газа на участке ускорения сопровождается имплозией. Возможность охлаждения рабочего тела со снижением энтропии без потерь энергии в окружающую среду, путём внутренней циркуляции тепла означает, что цикл Карно не является оптимальным, так как не учитывает подобные особенности неравновесной термодинамики:
|
|
|
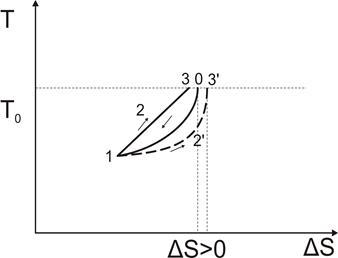
Рис. 7. Диаграмма ускорения и торможения теплопроводного газа.
Задача оптимального торможения теплопроводного газа и самоподдерживающийся поток. Видно, что налицо некий процесс 0-1 (рис. 7), который с позиции равновесной термодинамики требует отнятия тепла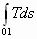 
в окружающую среду. Однако тепло 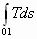уходит не в окружающую среду, а накапливается в нарастающем вдоль течения тепловом потоке. Следовательно, в процессе торможения газа, когда градиент температуры становиться положительным и 
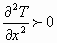, должен осуществиться процесс роста энтропии, который закончится тогда, когда поток полностью затормозится и наступит условие 
, 
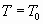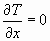. Данный процесс роста энтропии (линия 123) будет выражать собой кажущийся эффект нагрева, так как никакого притока тепла извне здесь не существует - в этом процессе лишь вновь возвращается к частицам газа отнятое потоком тепло:
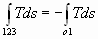. (11)
Таким образом, налицо процесс внутренней циркуляции тепла, который накладывает свой отпечаток на конечное значение энтропии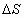 
. Ставится вопрос, как будет протекать процесс торможения газа и как изменится в итоге суммарная энтропия? Если процесс сжатия осуществляется в соответствии с линией 123, то в конце торможения - в точке 3 - давление торможения окажется выше исходного, а контур 01230 будет выражаться как цикл вечного двигателя второго рода, что “категорически недопустимо”. Согласно принципам классической термодинамики, данный процесс должен завершится ростом энтропии ( 
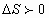), а соответствующая линия торможения должна проходить всегда ниже линии 0-1 ( линия 
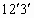). Вместе с тем, структура уравнений (8)-(9) свидетельствует, что в зависимости от характера ускорения (изменения площади потока) линию 0-1 можно изменять произвольно, и её форма может быть сильно искривленной – например, процесс торможения можно организовать так, что линия 123 будет выпуклой. Поэтому абсолютно непонятно, почему линия торможения должна проходить ниже линии ускорения 01.
На самом деле, как показано в работе [14], если теплопроводный газ ускоряется до сверхзвукового режима и затем появляется прямой скачок уплотнения, то, согласно условиям сохранения массы, энергии и импульса, процесс сжатия газа в прямом скачке в T-s координатах характеризуется линией, которая проходит выше линии ускорения, и конечное значение давления (точка 3) выше, чем начальное (точка 0) - таким образом, после разгона сильно теплопроводного газа до сверхзвукового режима может наступить течение, которое будет существовать бесконечно долго уже без применения нагнетателя! При этом будет осуществляться цикл вечного двигателя второго рода 01230, который вырабатывает энергию за счет поглощения тепла окружающей среды в процессе 3-0.
|
|
|
Из-за низкой теплопроводности реальных газов осуществление такого эффекта в малых масштабах невозможно, тем более, что в малых масштабах слабые положительные эффекты будут подавляться наличием трения. Но давайте рассмотрим течения больших масштабов. Во первых, при высоких числах Рейнольдса влияние трения резко падает. В условиях интенсивной турбулентности тепло распространяется очень быстро даже при малых градиентах температуры - это вызвано наличием турбулентной конвекции тепла. Следовательно, при интенсивной турбулентности газ приобретает свойства высокой эффективной теплопроводности. Вместе с тем, по имеющимся литературным данным, внутри торнадо скорость потока часто достигает сверхзвуковых значений. Следовательно, в вертикальном восходящем потоке вполне могут возникать скачки уплотнения и, помимо сосущего эффекта, который создаётся закрученным периферийным потоком, в центре торнадо можно предполагать наличие дополнительного самоподдерживающего эффекта, что ещё более усиливает устойчивость торнадо.
|
|
|
