 |
Особенности изменения энтропии в открытых неравновесных системах.
|
|
|
|
Особенности изменения энтропии в открытых неравновесных системах.
Как мы видели, процесс восстановления равновесия в замкнутом, изолированном пространстве сопровождается ростом энтропии, что отражает процесс деградации исходной системы. Описанный процесс находится в полном соответствии с требованиями второго закона в существующей формулировке. Вместе с тем, проведенный анализ показал, что в процессе изменения энтропии уровень механического неравновесия (градиенты плотности и давления) играет гораздо существенную роль, чем уровень температурной неуравновешенности. Такой результат позволяет поставить под сомнением теорию Карно и принципы энтропийного анализа тепловых процессов Клаузиуса, которые, при оценке предельной эффективности тепловых процессов, рассматривают упрощенную систему тел (Рабочее тело, источник тепла, охладитель), характеризующихся различными температурами.
Ниже мы увидим, что уровень механического неравновесия играет особенно существенную роль для открытых систем, и ее влияние дает результаты, которые противоречат существующей формулировке второго закона.
Рассмотрим объем сжимаемой жидкости с площадью поверхности 
(рис 2), который расширяется на величину 
. Средняя толщина данного элементарного объема определяется как соотношение:
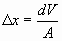. (19)
Естественно, что поверхность, которая выражается прерывистой линией на рис. 2, является условной. В реальности данная поверхность будет иметь другую форму, а приращение объема будет определяться из уравнения:
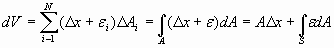. (20)
Рис. 2. Открытая термодинамическая система со свободной поверхностью.
Видно, что реальное изменение формы и объема рассматриваемой массы выражается малым отклонением 
, которое удовлетворяет условие:
|
|
|
. (21)
Предположим, что на поверхности объема действуют только силы давления. В таком случае, в процессе расширения, масса жидкости будет совершать работу:
. (22)
Давление 
, которое действует в произвольной точке поверхности, можно представить в виде суммы среднего по поверхности давления 
и локальногоотклонения 
, для которого соблюдается условие:
. (23)
Следовательно, элементарную работу можно определить из уравнения:
. (24)
Или, с учетом (21) и (23):
. (25)
Естественно, что если внутри рассматриваемого объема отсутствуют любые движения, кроме хаотических движений молекул, то данная работа может совершаться за счет внутренней тепловой энергии 
, и будем иметь:
. (26)
Последние уравнения позволяют заключить, что справедливо выражение:
. (27)
С другой стороны, путем дифференцирования (8) можно установить, что справедливо выражение:
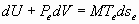. (28)
Что позволяет заключить, что, в отличие от процессов в замкнутом объеме, процессы в открытых объемах, со свободной поверхностью, сопровождаются изменением энтропии равновесного состояния, и данное изменение определяется из условия:
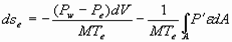. (29)
Последнее выражение является весьма интересным, так как, в отличие от случая замкнутых систем, оно противоречит принципам неуклонного роста энтропии и допускает нарушение второго закона в принятой формулировке. Действительно, из уравнений (21) и (23) следует, что функции и 
являются знакопеременными. При этом, из элементарных принципов механического равновесия, элементарные частицы будут расширяться интенсивно и будут иметь положительные отклонения ( 
) там, где они имеют положительное избыточное давление ( 
) и наоборот. Т. е. произведение 
, в большинстве случаев будет иметь положительное значение и должно соблюдаться условие:
. (30)
Уравнение (29) показывает, что разность между давлением на поверхности и внутри объема (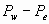 
) может оказать также весьма существенное влияние на характер изменения энтропии. Важность данного фактора подтверждается и другими методами анализа. В частности, влияние разности средних давлений на поверхности и внутри наглядно подтверждается при анализе течения газа в конических каналах с вращением потока.
|
|
|
Уравнение (29) позволяет сделать очень интересные выводы:
- В открытых теплоизолированных термодинамических системах поверхностные эффекты могут привести к снижению энтропии.
- В теплоизолированных термодинамических системах процессы изменения объема (адиабатные процессы) могут протекать изоентропно, если как внутри объема, так и на поверхности давление везде одинаково (
, 
). - В процессе изменения энтропии равновесного состояния теплоизолированной системы основную роль играет неравномерность давления внутри системы, а влияние неравномерности температуры не проявляется никак.
Естественно, что наличие теплообмена с окружающей средой и наличие движений внутри объема, вносит заметные изменения. Если предположим, что через ограничивающую поверхность рассматриваемого объема масса газа получает тепло ( 
), то суммарная энергия, которую получает жидкость извне, будет иметь значение 
. Рассматриваемая энергия будет вызывать изменение полной энергии жидкости, которая, в общем случае, представляет сумму внутренней энергии 
и кинетической энергии макроскопических движений вихревого и турбулентного характера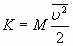 
, где - 
- средняя кинетическая энергия рассматриваемой массы газа. Соответственно, условие баланса энергии дает:
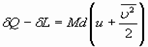. (31)
И вместо уравнения (26) будем иметь:
, (32)
Соответственно, для определения характера изменения энтропии равновесного состояния системы будем иметь:
. (33)
Для определения характера изменения энтропии неравновесной системы продифференцируем уравнение (16 ) и учтем (33):
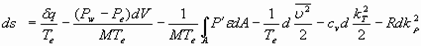. (34)
Как видим, первые три члена в правой части данного уравнения отражают внешние поверхностные воздействия. При этом первые два члена, в теплоизолированной системе, можно не учитывать. В таком случае третий член показывает, что изменение формы поверхности приводит к снижению энтропии. Последние три члена уравнения (34) отражают наличие кинетической энергии и неравномерности температуры и плотности. Уравнение подтверждает, что возникновение относительных движений в объеме и нарушение термодинамического равновесия приводят к снижению энтропии и наоборот, стремление системы к покою и равновесию сопровождается увеличением энтропии.
|
|
|
Проведенный анализ, в частности, позволяет заключить, что при быстром адиабатическом сжатии газа возникновение завихренности и нарушение равномерности параметров состояния приводит к процессу, который не является изоэнтропным. При этом вся парадоксальность такого процесса заключается в том, что в изолированной системе может происходить снижение энтропии.
Полученный теоретический результат подтверждает, что принцип неуклонного роста энтропии не является универсальным, и результат находится в согласии с работами тех ученых, которые отрицают существующую формулировку второго закона.
Чтобы ещё раз убедиться в правильности результата, проверим принятые нами допущения. Очевидно, что исходное уравнение сохранения энергии (31) не может подвергаться сомнению. Следовательно, правильность преобразования данного уравнения в уравнение (33) зависит от того, насколько правильно определена работа поверхностных сил 
. Как мы увидели, при определении данной работы нами было сделано допущение, что на ограничивающую поверхность действуют только силы давления. Отмеченное является единственным допущением, которое может повлиять на правильность полученного результата. В реальности, на поверхности объема действуют и вязкие силы, и для определения нужно учесть, что для определения потока механической энергии через ограничивающую поверхность нужно пользоваться полным удельным потоком механической энергии, который определяется как произведение тензора напряжений 
на локальную скорость 
:
. (35)
При этом нормальная составляющая данного вектора определяется как:
. (36)
где n - нормальный вектор поверхности.
Как известно, тензор напряжений можно выразить в виде суммы давления и тензора вязких напряжений 
:
|
|
|
. (37)
В таком случае за малый промежуток времени 
на единицу поверхности совершается работа:
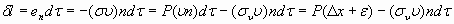. (38)
А работа по всей поверхности имеет значение:
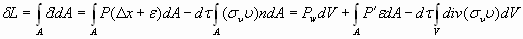. (39)
Учёт последнего уравнения вместо (25) позволяет заключить, что в реальных условиях изменение энтропии определяется из выражения:
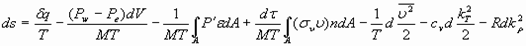(40)
Как мы видим, влияние реальных физических свойств газа проявляется в виде работы трения на поверхностности рассматриваемой системы, и данное трение может полностью перекрыть влияние тех эффектов, которые приводят к снижению энтропии. Вместе с тем, существует целый ряд процессов, в которых трение на поверхности незначительно. В частности, в работах [3, 4, 5] показано, что в течениях
больших масштабов влияние таких эффектов не ощутимо, и для открытых систем крупных масштабов нарушения второго закона можно воспринимать как вполне закономерное явление.
|
|
|
