 |
Диссипативный цикл быстрого сжатия и расширения
|
|
|
|
Диссипативный цикл быстрого сжатия и расширения
Если допустим, что в теплоизолированных процессах энтропия только растет, то процесс быстрого сжатия и расширения невозможно выразить в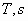 
координатах. Такая возможность создается только в том случае, если изменение энтропии происходит в соответствии с уравнением (40). При этом, для замкнутого объема в уравнении можно оставить только последние 3 члена:
(41)
Рис. 3. Цикл быстрого сжатия и расширения.
В процессе быстрого сжатия и расширения внутри объема появляется завихренность и неравномерность параметров состояния. Такой процесс можно выразить линиями 012 которые отражают кажущийся эффект охлаждения (рис. 3). В реальности, тепло от массы газа не отнимается, а соответствующая энергия переходит в энергию вихрей и термодинамических возмущении. Следовательно, в конце расширения, в точке 2, будем иметь энергию возмущении, которая соответствует площади под линией 012. Далее, если системе дадим возможность вернуться в состояние покоя в условиях постоянного объема, то энергия возмущений превратится в тепло, и будет происходить возрастание энтропии (линия 2-3). Возвращение в исходное состояние (точка 0) означает охлаждение газа (процесс 30), и в окружающее пространство будет выделяться тепло, которое равняется работе цикла (площадь цикла 0120).
Цикл быстрого сжатия и медленного расширения – «странный» цикл теплового двигателя
Как мы увидели, в процессе теплоизолированного сжатия теоретически можно наблюдать уменьшение энтропии. Роль теплового насоса в таком процессе играют возмущения внутри объема, которые способны аккумулировать тепловую энергию и создавать кажущийся эффект охлаждения.
|
|
|
Вместе с тем, если предположим, что процесс быстрого сжатия с уменьшением энтропии (процесс 01) существует, то приходим к явному нарушению второго закона термодинамики. Допустим, что процесс 01 существует, и состояние рабочего тела характеризуется точкой 1 (рис. 4), в таком случае, газ можно оставить в условиях постоянного объема 
сравнительно долго, и внутри объема наступит покой. Следовательно, энергия вихрей и других возмущений вновь превратится в тепло, и процесс будет выражаться линией 12.
Вся парадоксальность такого процесса заключается в том, что если газ расширим медленно (линия 23), то его температура в точке 3 будет ниже исходной температуры 
, и для возвращения в исходное состояние надо его нагреть за счет тепла окружающей среды (процесс 30). Т. е. налицо цикл двигателя, который вырабатывает энергию за счет природного тепла. В этом и заключается парадоксальность уравнения (40).
Рис. 4. Цикл быстрого сжатия и медленного расширения.
По нашему мнению, реальное осуществление такого цикла довольно трудно, так как относительно слабая энергия вихрей и термодинамических возмущений, по всей видимости, не сможет преодолеть затраты на трение механизма сжатия и расширения. Вместе с тем, приведенные рассуждения наглядно показывают, что человек может добывать энергию из равновесной окружающей среды.
Заключение.
Если внешние механические воздействия вызывают возмущения внутри системы, а трение с окружающими телами несущественно, то энтропия системы может уменьшаться. Следовательно, в теплоизолированных системах с внешним механическим воздействием процессы не всегда протекают с соблюдением принципа неуклонного роста энтропии, и может наблюдаться явное нарушение второго закона термодинамики.
|
|
|
