 |
Результаты и их обсуждения. Рис.1. Замкнутая неравновесная термодинамическая система.
|
|
|
|
Результаты и их обсуждения
В условиях неравновесия в термодинамических системах параметры состояния неодинаковы в различных точках пространства. Чтобы оценить уровень неравновесия таких систем, в первую очередь, следует внести понятие суммарной энтропии неравновесных систем.

Рис. 1. Замкнутая неравновесная термодинамическая система.
Если внутри ограниченного, замкнутого пространства (рис. 1) в произвольно выбранном малом объёме с массой 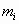 энтропия имеет значение
энтропия имеет значение 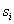 , то, как известно, суммарная энтропия системы, определяется как сумма энтропий всех частиц:
, то, как известно, суммарная энтропия системы, определяется как сумма энтропий всех частиц:
 . (1)
. (1)
Соответственно, среднее значение энтропии для такой неравновесной системы будет иметь вид:
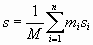 . (2)
. (2)
Как известно, для элементарной массы рабочего тела, внутри которой отсутствуют всякие движения, кроме теплового движения молекул, элементарное приращение энтропии определяется формулой:
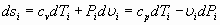 . (3)
. (3)
Соответственно, энтропия такой малой однороднойсреды определяется из уравнения:
 , (4)
, (4)
где 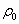 и
и  - выражают состояние среды, при котором энтропия равняется нулю. Обычно,
- выражают состояние среды, при котором энтропия равняется нулю. Обычно, 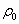 и
и  соответствуют параметрам окружающей среды. Учитывая последнее выражение, энтропию неравновесной системы можно определить из уравнения:
соответствуют параметрам окружающей среды. Учитывая последнее выражение, энтропию неравновесной системы можно определить из уравнения:
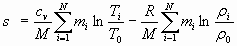 . (5)
. (5)
Проанализируем, на основе уравнения (5), как влияет наличие неравновесия на суммарную энтропию системы.
Влияние неравновесия на изменение энтропии в замкнутой системе постоянного объема. Замкнутая неравновесная система, представленная на рис 1, при отсутствии постоянно действующих возмущений, не может существовать стабильно, и она постепенно превратится в равновесную систему, путем выравнивания давления и температуры по всему объему. Из элементарных условий сохранения энергии и массы следует, что после выравнивания параметров рабочее тело в объеме будет иметь температуру и плотность, которые определяются из уравнений:
|
|
|
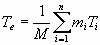 , (6)
, (6)
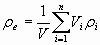 . (7)
. (7)
Отмеченные параметры выражают состояние равновесной среды в данном объеме, и они будут сохраняться сколь угодно долго, если замкнутый постоянный объем одновременно является и теплоизолированным. Энтропия равновесного состояния такой системы будет определяться из уравнения:
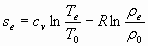 . (8)
. (8)
Определим, как изменяется энтропия системы в процессе восстановления равновесия, или в процессе выравнивания параметров состояния - для этого надо определить разность 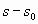 на основе уравнений (5) и (8):
на основе уравнений (5) и (8):
 . (9)
. (9)
При умеренных относительных отклонениях температуры и плотности (в пределах 10-15 %) с достаточно высокой точностью можно применять приближение:
 , (10)
, (10)
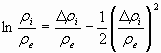 . (11)
. (11)
С учетом (6) будем иметь:
 . (12)
. (12)
Соответственно, при сравнительно малых отклонениях, приращение энтропии будет определяться из уравнения:
 . (13)
. (13)
или
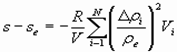 (14)
(14)
Последние выражения позволяют сделать интересные выводы:
1. В изолированной системе энтропия неравновесного состояния ниже, чем ее энтропия в равновесном состоянии.
2. Малые отклонения температуры в неравновесной системе не вызывают ощутимые изменения энтропии в процессе восстановления равновесия.
3. На характер изменения энтропии газовой среды уровень механического неравновесия (разность плотностей или разность давления) оказывает гораздо существенное влияние, чем уровень теплового неравновесия (разность температур).
Как видим, в интегральном виде уравнение (9) имеет вид:
 . (15)
. (15)
Если предположить, что отклонения малы, то с учётом (10)-(11) получим:
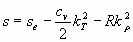 . (16)
. (16)
 . (17)
. (17)
 . (18)
. (18)
Таким образом, при малых возмущениях приращение энтропии зависит от коэффициентов, которые выражают неравномерность параметров состояния, или уровень неравновесия системы. Следует учитывать, что при малых отклонениях плотности в газовой среде (в воздухе) отклонения температуры примерно 2, 5 раза ниже, чем отклонения плотности, а среднеквадратичные отклонения отличаются почти на порядок, поэтому в правой части уравнения (16) второй член значительно отстаёт от третьего. Следовательно, уравнение (16) по своему смыслу совпадает с уравнением (13) и показывает, что при малых отклонениях от равновесия изменения плотности (или давления) играют более существенную роль, чем изменения температуры.
|
|
|
|
|
|


