 |
Понятие о частотных характеристиках.
|
|
|
|
Частотные характеристики звеньев и систем отражают зависимость установившихся параметров выходного сигнала для гармонического входного воздействия, при изменении частоты входного сигнала ω от 0 до ∞.
Пусть на вход звена или системы подается входной сигнал: x(t)=Aвхejωt, e±α = cosα ± jsinα ф-ла Эйлера. α=П, то eп+1=0. Если система устойчива, то с течением времени на выходе устанавливается колебания той же частоты, но с другой амплитудой и фазой. y(t)=Aвыхe(jωt+φ). Свяжем это решение с диф. ур-ем системы: dy/dt=pY=d/dt(Aвыхe(jωt+φ)) = Aвых (jω)ejωt+φ = (jω)*y; d2y/dt2=p2Y=…= (jω)2*y; dny/dtn =pnY=…= (jω)n*y. dx/dt=pX=d/dt(Aвхejωt) =Aвх(jω)ejωt = (jω)*x; d2x/dt2=p2X=…= (jω)2*x; dmx/dtm =pmx=…= (jω)m*x. Подставив найденое выр-е в ур-е an* (dny (t) /dtn) + an-1*(dn-1y(t)/dtn-1)+…+ a1*(dy(t)/dt)+ a0 *y(t) = bm*(dmu(t)/dtm) + bm-1* (dm-1 u(t)/dtm-1)+…+ b1*(du(t)/dt)+ b0*u(t) получим [an*(jω)n + an-1*(jω)n-1 +…+ a1*(jω)+ a0]*y = [bm*(jω)m + bm-1*(jω)m-1 +…+ b1*(jω)+ b0]*u, D(jω)* Aвыхejωt+φ = K*(jω) Aвхejωt. Комплексный коэфф. передачи звена или системы будет равен: Aвыхejωt+φ/ Aвхejωt =K(jω)/D(jω) = (Aвых/Aвх)* ejφ = W(jω). Эта ф-я назыв. комплексно частотной хар-ой (или амплитудно фазовая хар-ка) АФХ, КЧХ. Для каждого значения частоты ω, ф-я W(jω) представляет собой комплексную ф-ю (число), модуль которого равен отношению амплитуды вх. сигнала к амплитуде вых. сигнала, а аргумент равен углу сдвига фазы вых. сигнала относительно входного.
Ф-ю можно представить в виде вектора комплексной плоскости:
|
поворачиваться и его годограф будет представлять собой геометр. образ КЧХ или АФХ. Для отрицательных знач-й частот ω от 0 до -∞, график АФХ будет выглядеть зеркально относительно вещественной. Выводы: а) аналитически выражение АФХ и КЧХ формально можно получить из передат. ф-ии подстановкой в место p=jω. б) АФХ может быть получено экспериментально: 1.1
|
|
|
подаем на вход сигнал т.е x(t)=Aвыхsinωt. 1.2 после установления колебаний на выходе измеряем Авых, Авх, ω1, φ(ω1). 1.3 вычисляем модуль А(ω1)=Авых/Авх и строим т.АФХ
1.4 Повторяемопыт для ω2, ω3, ω4,… и соеденим точки пунктирной линией (рис). Как любая комплексная ф-я АФХ
может быть записана в показат. и в алгебраичской форме: W(jω)=A(ω)ejφ(ω) = P(ω) +jQ(ω). A(ω)-АЧХ- зависимость отношения амплитуды вых. сигнала к амплитуде вход. сигнала от частоты. φ(ω) –ФЧХ- зависимость сдвига фазы выходного сигнала от частоты. Р(ω)- ВЧХ(веществ. част. хар.). Q(ω)-МЧХ- мнимая частотная хар-ка.
A(ω)= P2(ω)+ Q2(ω);
φ(ω)=arctg(Q(ω)/P(ω));
P(ω)=Aωcosφ(ω); Q(ω)=A(ω)sinφ(ω). В инжинерной практике
широко применяются ЛЧХ. Для построения частотных хар-к в логарифмическом масштабе используют спец-е еденицы. В качестве еденицы логарифмического масштаба АЧХ используется [дБ]. L(ω)=20ℓgA(ω).
Для логарифмической еденицы частоты наибольшее распространение в автоматике получила Декада.
 |
Одна декада соотв-ет изменению частоты ω в 10 раз.
Типовые динамические звенья (временные и частотные характеристики, передаточные функции).
|
|
При исследов. сложных технич. систем широко применяется принцип декомпозиции тюе разбиение сложного на простые составляющие. Теория управ-я использует разбиение сложных САУ на элементарные звенья назыв. типовыми динамическими звеньями. Типовыми назыв. звенья динамика которых описыв. диф. ур-ми не выше второго порядка. Для описания большинсва реально технических систем достаточно типовых динам. звеньев: 1) Безинерц. усилит. звено: m=0, n=0 (b1=0, a2= a3=0). a0Y(t)=b0X(t). Выходной сигнал пов-яет без искажения по ф-ме и без сдвига по времени входной сигнал|
|
|
у(t)=(b0/a0)*x(t), b0/a0=k[ед.изм.вых/ед.изм.вх.];
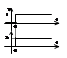x(t)=1(t), h(t)=k*1(t)
OФ: Y(p)=kX(p);
ПФ: W(p)=Y(p)/X(p)=k;
АФХ: W(jω)=k;
ВЧХ: P(ω)=k;
МЧХ: Q(ω)=0;
АЧХ: A(ω)= P2+Q2 =P
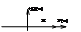ФЧХ: φ(ω)=arctgQ/P=artcg0=0.
АФХ
2) Инетгрирующее звено: m=0,n=1,a0=0. a1p*Y= b0x. a1*(dy/dt)=b0x/a1, b0/a1=Kи [1/c]-коэф. добротности. 1/Ки=Ти [c], ∫dy=∫Киxdt, y(t)=Ки∫xdt.
Ω=dα/dt, α=∫Ωdt. W(p)= Zoc/Zвх, Zвх=R, Zвх=1/Cp, Rc=Tи. W(p)=1/Rcp=1/Тиp= Ки/р. П.Х. x(t)=1(t),
y(t)=Ки∫1dt = Ки*t=t/Ти.Ки- коэф. добротности влияет на наклон переход. характеристики. Ти- равно времени за которое входная величина
меняется на1. dy/dt=Ки*х. p*Y= Ки*х. ПФ. W(p)
=Y(p)/X(p)=Ки/p=1/Тир- перед. ф-я
интегрирующего звена. АФХ W(jω)=1/jTω=-j* 1/Tω. Видно что АФХ расположена на отриц. мнимой оси.
ВЧХ: P(ω)=0; МЧХ: Q(ω)=-1/Tω; АЧХ: A(ω)= P2+Q2 =|Q|, A(ω)=1/Tk*ω=Ки/ω; ФЧХ: φ=arctgQ/P =arctg(-∞)=-П/2. A(ω)=Ки/ω, L(ω)=20lgA(ω)= 20lgКи - 20lgω. L(1)=20lgКи. 3) Дифф-ое звено
описывается уравнением: a1*(dY/dt)+ a0Y = b1*(dY/dt) или a1*PY+a0*Y=b1*PX, в канонической форме: (TP+1)Y=KPX где T=a1/a0, K=b1/b0, передат-я ф-я звена Y/X=Wрд(p)=K*P/T*P+1. Реальные дифференцирующие звенья имеют такую передаточную функцию. Очевидно, что чем меньше Т, тем ближе реальное звено по свойствам приближается к идеальному.
4) Апериодич. звено I-го порядка
a1*(dY/dt)+ a0Y = b0Х. Это уравнение является линейным дифференциальным уравнением первого порядка. Для того, чтобы определять свойства звена по величине его параметров, уравнение представляется в канонической форме
T*(dY/dt)+Y=K*X или TPY+Y=K*X, где T= a1/a0 [c]-пост. врем. Звена, K=b0/a0-коэф. передачи звена. В частности, при T ® 0 получаем безинерционное звено. Получаем: Y/X= Wа(p)=K/TP+1 5) Интегрир. звено II-го порядка: а) апериод. звено II-го порядка, б) колебат. звено II-го порядка:
описыв. ур-ем a2*(dY2/dt2)+ a1*(dY/dt)+ a0Y = b0*Х но не выполн. условие а2р2+ а1р+ а0=0, тогда в канонической форме T2P2Y2+ 2ρ*TPY=КХ, где Т
= a2/a0 – пост. времени, ρ=а1/2* а2 – показ. колебательности,
|
|
|
|
τ=ℓ/υ, y(t)=χ(t-τ),
h(t)=1(t-τ). В
операт. виде:
y(t)=х(t-τ), Y(p)=
X(p)e-τp. ПФ: W(p) =
Y(p)/X(p)=e-τp; АФХ: W(iω)=e-τiω=cosωτ – jsinωτ; ВЧХ: P(ω)=cosωτ; МЧХ:Q(ω)=-sinωτ; АЧХ: A(ω)=
|
P2+Q2 = cos2ωτ+sin2ωτ =1; ФЧХ: φ(ω)=arctgQ/P = arctg –sinωτ/cosωτ = -arctg tgωτ=-ωτ; ЛАЧХ: L(ω)=20lg(ω)=0.
|
|
|
