Преобразование структурных схем САУ. Связь структурных схем с графами.

Любую САУ можно рассматривать как комбинацию динамических звеньев. Изображение САУ в виде совокупности динамических звеньев с указателями связей между ними назыв. структурной схемой. 1) звено с 1 входом и выходом для него Y(p)=W(p) *X(p) 2) звено с 2-мя входами

 

для него Y(p)=W1(p)*X1(p)+ W(p)*X2(p). Его можно представить и в другом виде:

 

3) Узел х1=х2=х3

 

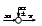
4) Сумматор y=x1±x2

или или

 

Правило преобраз. структурных схем: 1) перестановка однотипных элементов: а) узлы с узлами, б) сумматоры с сумматорами, в) звенья со звеньями:

 

= =

 

 

 

= 2) Перенос узла череззвено: а) с выхода на вход б) со входа

на выход =

 

=

 

Х3

Х1

W1

3) Перенос сумматора через звено: а) со входа на выход б) с выхода на вход =

Х2

 

 

у

х

W(р)

Структурные схемы САУ могут быть изображены в виде сигнальных графов. Def Графом назыв. множество вершин и ребер. Каждому ребру соотв. 2 вершины: начало и конец ребра. Каждая вершина отмеченная на графе кружком или точкой соотв. некоторой переменной рассматр. системы. Каждое ребро изображается в виде линии со стрелкой указывающее направление прохождения сигнала, имеет вершину начало вход. вел. и вершину конец выходной вел. Между структурной схемой и графом имеется след-е соотв-е: прямоуг-к структ-ой схемы соотв. ребру графа, а стрелки на структ-й схеме соотв. вершинам графа его граф

Пример:

 

 

 

Передаточные функции группы звеньев при последовательном, параллельном и встречно-параллельном соединении звеньев.

1) Последовательное соед. Называется соединение при котором выходной сигнал предыдущего яв-ся входным для последующего.

 

 

Y_i(p)=W_i*X_i(p), x=x1, x=x2, y=y3, y3=y. Y(p)= Y₃(p)= W₃(p)*X₃(p)=Y₂(p)*W₃(p)=W₂(p)*W₃(p)* X₂(p)=W₂(p)*W₃(p)*Y₁(p)=W₁(p)*W₂(p)* W₃(p) * X(p). W_э(p)=Y(p)/X(p)=W1(p)*W2(p)*W3(p)=

Πⁿ_i=1Wi(p). Вывод: П.Ф. группы послед. соед. звеньев = произв. передат. ф-ий отдельных звеньев. 2) Параллельное соед. Назыв. соединение при котором входной сигнал яв-ся общим для всех звеньев, а выходной яв-ся суммой всех выходных звеньев.

Y_i(p)=W_i*X_i(p), x=x1=x2=х3; y=y1=y2=y3. Y(p)=Y₁(p)+ Y₂(p)+Y₃(p)=W₁(p)*X(p)+ W₂(p)*X(p)+W₃(p)*X(p) = [W₁(p)+W₂(p)+W₃(p)]*X(p).

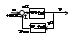W_э(p)=Y(p)/X(p)=W₁(p)+W₂(p)+W₃(p)=Σⁿ_i=1W_i(p). П.Ф. группы параллельно соед. звеньев равна сумме отдельных параллельных звеньев. 3) Встречно- параллельное соед. (Соед. с ОС)

Схема при которой сигнал с выхода звена или всей системы через какое-либо другое звено подается

опять опять на вход назыв. соед. с обратной связью. Если сигнал обрат. связи складыв. со входным, то ОС назыв. положительная, если вычит. то отрицательная. х1=х±у_ос. y(p)=W₁(p)* X₁(p), x₁=x±y_oc, Y_oc(p)=W_oc(p)*Y(p). Y(p) = W₁(p)* X₁(p)= W₁(p)* X(p)± W₁(p)* Y_oc(p)= W₁(p)* X(p)± W₁(p)* W_oc(p)* Y(p). [1±W₁(p)*W_oc(p)]Y(p)= W₁(p)* X(p). W_э(p)=Y(p)/X(p)= W₁(p)/1±W₁(p) * W_oc(p). Частный случай: 1-я обратная связь.

W_з(p) = W_р(p)/1+W_р(p), W_oc(p)=1.

 

 

14. Передаточные функции замкнутой САУ по управлению, по возмущению и по ошибке.

Uз

а) передаточная

ф-я разомкн-й

системы. Размыкаем главную

обратную связь,

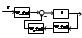тогда выходной сигнал будет равен суперпозиции реакции системы на возмущ. и управ-ее воздействие. Y(p)=W_y(p)*W_oy(p)* U_з(p)+W_of(p)* f(p). Обозначим W_y(p)* W_oy(p)= W_p(p) как W_p(p)= M(p)/D(p).- предат. ф-я разомкнутой системы. б) П.Ф. замкнутой системы по управленитю f=0. W_зу(p)=Y(p)/U_з(p)=W_р(p)/(1+W_р(p)*W_д(p))= учитывая W_p(p)= M(p)/D(p) получим = M(p)/(D(p)+M(p)*W_д(p)). в) П.Ф. замкнутой системы по возмущению. U_з=const. Вход-f, выход-Y.

W_зf(p)=W_of(p)/(1+ W_p(p)*W_д(p))= учитывая W_p(p)= M(p)/D(p)

получим = D(p)*W_зf(p)/(D(p)+M(p)*W_д(p)). г) П.Ф. замкнутой системы по ошибке Е, f=0, Выход -Е, Вход-U_з(p).

W_зЕ(p)=1/(1+ W_p(p) * W_д(p))= учитывая W_p(p)= M(p)/D(p)получим =

 

D(p)/(D(p)+M(p)*W_д(p)).

 

 

Понятие устойчивости САУ.

Под действием возмущений управ-я вел-на отклоняется от заданного состояния. В ответ на это УУ (регулятор) формирует управл-е воздействие на объект стремясь вернуть регулир-ую величину к заданному значению. В результате совместного действия управл-его и возм-его воздействий в системе происходит переходный процесс. Возможны 4 варианта его протекания: 1) с течением времени управл-я велич. возвращается с некоторой точностью в заданное равновесное состояние. Такой переходный процесс назыв. сходящимся, а система устойчивой.

Геометр. интерпретация системы:

 

 

2) Система не может восстановить равновесное состояние. Управляемая вел-на все больше удал-ся от заданного значения. Такой перех. процесс назыв. расходящимся, а система не устойчивой.

Геометр. интерпр.

 

3) Пограничный между 1и2. В системе возникают незатухающие колебания регулируемой величины. Такой перех. процесс назыв. незатух-им колебат., а система считается находящимся на границе устойчивости.

Геометр. интерпр.

 

4) В системе не возникает переходного процесса. Значение управл. переменной остается на том же уровне при котором оно достигло под действ. возмущения. Это будет нейтрально устойчивая система.

Вывод: устойчивость- это способность САУ возвращаться с некоторой точностью в заданное равновесное состояние после того как она была выведена из него в результате какого-либо воздействия. Более точная математ-я формулировка понятие точности принадлежит А.А. Ляпунову. Def невозмущенное движение y(t) (установив. режим) будет устойчивым если для любого наперед заданного положительного числа δ как бы оно мало не было можно выбрать другое положит. число λ(δ) такое что для любого возмущения удовлет. условию: Σⁿ_i=1Δ²f_io< λ(δ), то возмущенное движение будет удовлет. условию Σⁿ_i=1Δ²y_i<δ начиная со времени t>t₀. Геометр. это выглядит так:

Эта формулировка отражает то что при нарушении равновесия абсолютная величина отклонения управляемой переменной

должна по истечению достаточно длительного промежутка времени стать меньше некоторого заранее заданного числа δ. Понятие устойчивости можно сформулировать: линейное САУ назыв. устойчивой если ее выходная величина остается огран. при любых ограниченных по величине возмущениях. Следует отметить что геометр. интерпретация устойчивости соотв. линейным системам. Реальные системы как правило не линейны и характер устойчивости САУ может иметь след. вид:

Определение устойчивости САУ: а) прямые т.е путем решения диф. ур. системы и анализа системы, б) по корням харак-го

уравнения, в) с помощью критерия устойчивости.

 

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: