Дифференциальные уравнения равновесия жидкости. Основное уравнение гидростатики.

 

Выделим в покоящейся жидкости при точке А элементарный объем в виде параллелепипеда и составим условия его равновесия (рис.2).

Рис 2

 

На параллелепипед действуют поверхностные силы гидростатического давления и объемные силы. Если принять, что давление в центре параллелепипеда в точке А равно p_A, то давление в центре левой грани p₁ будет:

,

 

а сила давления на всю грань

.

 

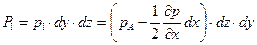Аналогично, сила давления на правую грань:

 

.

 

Здесь 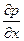- изменение гидростатического давления по оси х на единицу длины. Знак этой величины определяется направлением перемещения от точки А к граням. Объемные силы в проекции на ось х будут равны ρXdxdydz.

Тогда уравнение равновесия будет

 

.

 

Подставляя значения P₁ и P₂ и приводя подобные члены, получим

- ,

 

или, сокращая на объем параллелепипеда dxdydz, получим уравнение, в котором действующие силы отнесены к единице объема жидкости

 

.

 

Уравнения равновесия для других осей координат напишем по аналогии:

(3.1)

.

 

Эти уравнения называются уравнениями Эйлера. Они показывают, что в состоянии покоя массовые силы, действующие на каждую частицу жидкости, уравновешиваются поверхностными силами (градиентами давления).

Для вывода основного уравнения гидростатики необходимо проинтегрировать полученные дифференциальные уравнения равновесия. Поэтому умножим каждое из уравнений Эйлера на dx,dy,dz соответственно и сложим почленно. В результате получим:

(3.2)

 

Очевидно, что правая часть уравнения представляет собой полный дифференциал давления dp, поскольку p=f(x,y,x),а так как ρ=const, то выражение в скобках левой части уравнения есть также полный дифференциал некоторой функции координат U=f(x,y,z), называемой силовой функцией. Эта функция обладает свойством:

 

 

Cилы, для которых такая функция существует, называются силами имеющими потенциал.

С учетом изложенного общее уравнение равновесия (3.2) можно записать в виде:

.

 

Следовательно, несжимаемая жидкость может находиться в равновесии только под действием объемных сил имеющих потенциал. К таким силам, в частности, относится сила тяжести и, если она является единственной из действующих массовых сил, то можно записать

 

X=0, Y=0, Z=-g,

 

и уравнение равновесия будет:

 

-ρgdz=dp или γdz=dp.

 

После интегрирования, считая γ = const, получим:

 

или . (3.3)

 

Отсюда видно, что давление в покоящейся жидкости есть функция одной координаты z. Располагая теперь начало координат на поверхности жидкости, где p=p₀, а z = O, получим для таких граничных условий, что const = -p_0. Подставляя это значение в (3.3) и используя новую переменную - глубину погружения h = - z, получим основное уравнение гидростатического давления

или . (3.4)

 

Следовательно, давление в любой точке жидкости, находящейся под действием силы тяжести, складывается из давления на поверхности и произведения объемного веса жидкости на глубину погружения данной точки. Из уравнения видно, что давление - линейная функция глубины погружения.

В открытых сосудах или водоемах давление на поверхности равно атмосферному, т.е. p₀=p_атм. В этом случае слагаемое γh называется избыточным давлением p_изб, а давление p - абсолютным давлением

 

p_абс=p_атм+γh.

 

Если давление в какой либо точке оказывается ниже атмосферного, т.е. p<p_атм, то разница между атмосферным давлением и давлением в этой точке называется вакуумом

 

p_вак=p_атм-р.

 

Избыточное и вакуумметрическое давление измеряются пружинными приборами - манометрами и вакуумметрами или с помощью трубок (пьезометров), присоединяемых к месту измерения давления. Пьезометры измеряют давление в единицах высоты (длины) подъема жидкости в трубках. Поэтому его называют пьезометрическим давлением или напором. Линейная размерность напора связана с размерностью напряжения простым соотношением:

или .

 

Пьезометрическое давление, отнесенное к какой-либо плоскости сравнения, называют гидростатическим напором относительно этой плоскости. Оказывается, что гидростатический напор для всех точек объема покоящейся жидкости одинаков. Действительно, для показанных на рис.3 точек А и В можно написать:

Рис.3

 

p_A=p_o+ρgh_A и p_B=p₀+ρgh_B,

 

а напор относительно плоскости сравнения О-О запишется так:

 

,

 

.

 

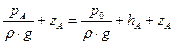Так как правые части равны, то

 

,

 

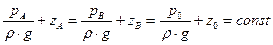или в общем виде

(3.5)

 

Это соотношение выражает гидростатический закон распределения давления в покоящейся жидкости.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: