 |
Обобщение уравнения Бернулли на целый поток реальной жидкости. Диаграмма уравнения Бернулли. Гидравлический и пьезометрический уклоны.
|
|
|
|
При выводе уравнение Бернулли для идеальной жидкости не учитывалась энергия, затрачиваемая на преодоление сил трения, возникающих при движении реальной (вязкой) жидкости. В случае реальной жидкости начальная энергия не остается постоянной по длине струйки или целого потока (состоящего из множества струек), а уменьшается в направлении течения из-за необратимого преобразования части механической энергии в тепловую энергию. Последняя безвозвратно рассеивается в окружающее пространство. Общие потери энергии в потоке складываются из потерь энергии отдельных элементарных струек. Величину энергии, потерянной целым потоком, отнесенную к единице веса протекающей жидкости, будем обозначать как hпот..
При распространении уравнения Бернулли на целый поток реальной жидкости кроме потерь необходимо учитывать ещё то обстоятельство, что скорости струек по сечению потока различны - у стенок или дна они меньше, а к центру потока увеличиваются. Поэтому в член уравнения Бернулли, выражающий удельную кинетическую энергию потока, вводится среднее по сечению потока значение скорости - υ.
Тогда уравнение Бернулли запишется так:
,
или
.
Вместе с тем, кинетическая энергия потока, рассчитанная по средней скорости (К.Э.)ср., не равна сумме кинетических энергий элементарных струек составляющих поток Σ(К.Э.)струек. Последняя оказывается больше, в связи с чем, в первый член уравнения Бернулли приходится вводить поправочный коэффициент α, называемый коэффициентом кинетической энергии или коррективом скорости
,
где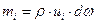 
- масса отдельных струек, 
- масса всего потока жидкости.
Для турбулентного течения в трубах и открытых каналах коэффициент α изменяется в пределах 1.02 – 1.12, в связи с чем, обычно принимается равным 1.0, а для ламинарных режимов течений, имеющих большую неравномерность распределения скоростей по сечению α = 2.0.
|
|
|
Что касается пьезометрического 
и геометрического напоров z, то их сумма для параллельно струйного или плавно изменяющегося движения, так же как и в гидростатике постоянна для всех точек поперечного сечения потока и, следовательно, при обобщении уравнения Бернулли на целый поток реальной жидкости запись этих членов не изменяется.
Таким образом, с учетом предыдущих замечаний, уравнение Бернулли для потока реальной жидкости при установившемся движении записывается в следующем виде:
, (9.1)
или
.
Так как в такой форме записи все члены уравнения Бернулли имеют линейную размерность, т.е. представляют собой напоры или высоты (§8), то в любом сечении потока произвольного очертания эти напоры можно отложить в виде соответствующих отрезков (рис.10):
Геометрический напор z отсчитывается от условной плоскости сравнения 0-0 до оси потока, далее вверх откладываются отрезки равные пьезометрическому напору и скоростному напору 
. Концы соответствующих отрезков в разных сечениях по длине потока соединяются линиями, которые называются пьезометрической линией и линией полной энергии. Константа в правой части уравнения Бернулли, характеризующая начальный запас энергии, образует горизонтальную линию начальной энергии. Расстояние между линиями полной и начальной энергий представляет собой потерянный напор hпот..
 |
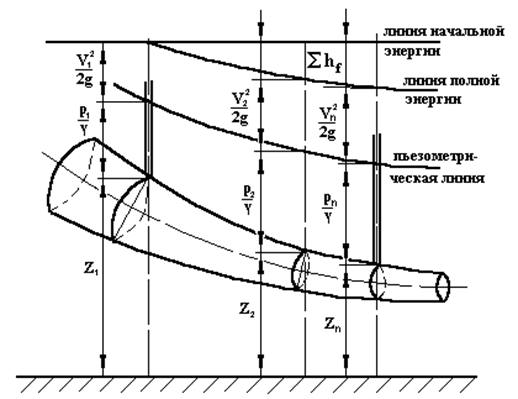Рис.10
Построенная диаграмма наглядно иллюстрирует преобразование удельной энергии потока при его движении, показывает переход одного вида энергии в другой. Например, при расширении поперечного сечения потока происходит увеличение потенциальной энергии давления (пьезометрического напора), а кинетическая энергия (скоростной напор) уменьшается. Обратная картина наблюдается при уменьшении сечения потока.
|
|
|
Важным обстоятельством является тот факт, что пьезометрическая линия по длине потока может повышаться и понижаться, в то время как линия полной энергии из-за непрерывного увеличения потерь постоянно снижается.
Падение линии полной энергии на единицу длины потока l называется гидравлическим уклоном i и выражается формулой:
. (9.2)
Следовательно, величина гидравлического уклона характеризует уменьшение полной удельной энергии потока.
Понятие уклона можно ввести и для пьезометрической линии. В этом случае уклон называется пьезометрическим и обозначается i*:
. (9.3)
Пьезометрический уклон может быть как положительным, так и отрицательным. В частном случае равномерного движения, когда скорость по длине потока постоянна, очевидно, что i = i*. Обычно это имеет место при напорном движении жидкости в трубах.
|
|
|
