 |
Давление на цилиндрические поверхности. Закон Архимеда
|
|
|
|
Выделим на цилиндрической поверхности произвольный участок АВ и найдем действующую на него силу гидростатического давления (рис.5)
 |
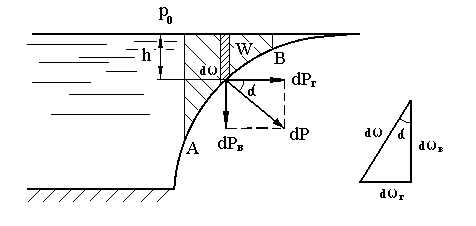Рис.5
На рассматриваемой поверхности возьмем элемент площади dω, кривизной которого можно пренебречь, и найдем действующую на него силу давления.
.
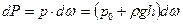Разложим эту силу на вертикальную и горизонтальную составляющую.
,
,
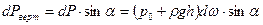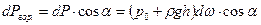но из рис.5 видно, что
,
.
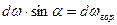Следовательно,
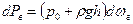
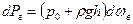. (5.1)
Используя эти зависимости, найдем сначала горизонтальную составляющую силы гидростатического давления на цилиндрическую поверхность
.
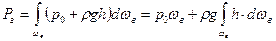Интегрирование производится по площади проекции цилиндрической поверхности АВ на вертикальную плоскость, т.е. по площади - ωв.
Второе слагаемое является статическим моментом площади ωг относительно оси, проходящей через точку О перпендикулярно плоскости чертежа. Его можно представить так:
,
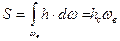где hс - глубина погружения центра тяжести площадки ωв. Тогда
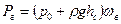. (5.2)
Определим теперь из (5.1) вертикальную составляющую силы давления
.
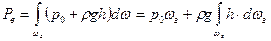Здесь ωг - проекция цилиндрической поверхности АВ на горизонтальную плоскость. Произведение hdωг во втором слагаемом представляет собой заштрихованный на рисунке элементарный объем, а значение интеграла равно всему объему, находящемуся над поверхностью АВ (на рисунке он показан крупной штриховкой). Таким образом
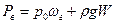. (5.3)
Полная сила Р гидростатического давления на цилиндрическую поверхность определяется составляющими Рг (5.2) и Рв (5.3) по правилу параллелограмма:
.
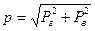Направление силы Р определится углом α, причем
.
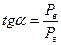Для цилиндрической поверхности сила Р всегда проходит через центр кривизны, так как все элементарные составляющие нормальны к поверхности стенки и проходят через ее центр тяжести.
|
|
|
При практическом определении вертикальной составляющей силы гидростатического давления необходимо знать общее правило, по которому находится объем тела давления. Объем тела давления ограничивается: цилиндрической поверхностью, двумя вертикальными плоскостями, проведенными из концов цилиндрической поверхности до свободной поверхности жидкости (рис.6-а) или ее продолжения (рис.6-б).
Из рисунка видно, что в первом случае объем тела давления находится внутри жидкости (действительное тело давления), а во втором - вне ее (фиктивное тело давления). Направления вертикальных составляющих оказываются противоположными, а величина их равна весу жидкости, находящейся в объеме тела давления.
 |
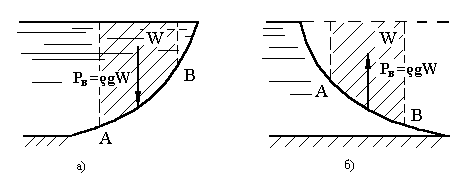Рис.6
Рассмотрим теперь погруженное тело произвольной формы (рис.7) и определим силы давления на него в проекциях на оси координат.
 |
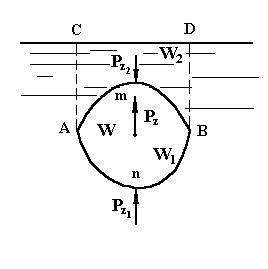Рис 7
Горизонтальные составляющие силы давления Рx будут одинаковы с обеих сторон тела, поскольку проекция его боковой криволинейной поверхности на вертикальную плоскость ωв, взятая справа и слева, будет одна и та же, Аналогично этому будут одинаковы и горизонтальные составляющие Рy в направлении оси y. Значит, горизонтальные составляющие сил гидростатического давления взаимно уравновешиваются и не влияют на равновесие погруженного тела. Вертикальные же составляющие будут различны. Действительно, сила давления на нижнюю часть поверхности тела Рz1,т.е. на поверхность АnВ будет направлена вверх и равна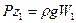 
, где W1 - объем, ограниченный поверхностью ACDBn. Сила давления на верхнюю часть тела Pz2, т.е. на поверхность AmB будет направлена вниз и равна 
, где W2 - объем, ограниченный поверхностью ACDBm. Результирующая вертикальная составляющая силы давления будет равна их разности, т.е.
|
|
|
,
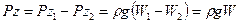где W - объем тела.
Полученная формула выражает закон Архимеда, согласно которому на тело погруженное в жидкость, действует направленная вверх выталкивающая сила, равная весу жидкости, вытесненной этим телом.
Из закона Архимеда следует условие плавания тел. Если вес тела G>ρgW, то тело тонет; при G<ρgW - тело всплывает; когда G=W, - тело находится во взвешенном состоянии.
Введение в гидродинамику.
Гидродинамикой называется раздел гидравлики, в котором изучаются законы движения жидкости. Эти законы сложнее законов покоящейся жидкости, состояние которой характеризуется лишь величиной гидростатического давления. При движении состояние жидкости определяется не только давлением, но и величинами и направлениями скоростей и ускорений отдельных частиц жидкости. Задача гидродинамики - установление связи в движущемся потоке между давлением и кинематическими характеристиками потока. Величины давлений, скоростей и ускорений могут изменяться в зависимости от времени и координат рассматриваемой точки. В связи с этим различают:
а) Установившееся и неустановившееся движение.
Если скорость и давление (напор) в любой точке потока несжимаемой жидкости с течением времени остаются неизменными, то такое движение называется установившемся. При установившемся движении скорость и давление зависят только от координат точки, т.е.
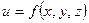и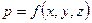 
.
Если давление и скорость в потоке зависят кроме координат ещё и от времени, т.е.
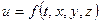и 
,
то такое движение называется неустановившимся. Примерами неустановившегося движения могут служить разгон или торможение жидкости в трубе при включении (выключении) насоса, движение воды во время паводка, истечение жидкости из резервуара через отверстие или сливную трубу и т.п.
б) Равномерное и неравномерное движение.
Равномерным называется движение, при котором скорости в сходственных точках поперечных сечений по длине потока не изменяются. Такое течение возможно в каналах постоянного сечения и трубах. Если же скорость по длине потока изменяется, то такое движение называется неравномерным. Такой характер движения наблюдается в реке при её сужении и расширении, на крутых поворотах, а также в конфузорах и диффузорах.
|
|
|
в) Напорное и безнапорное движение.
Напорным движением называется такое движение, при котором поток со всех сторон ограничен твердыми стенками (обычно течение в трубах при полном их заполнении). Движение происходит за счет избыточного давления, создаваемого насосом или водонапорным баком.
Движение, при котором поток лишь частично ограничен твердыми стенками и имеет свободную поверхность, называется безнапорным. Давление на свободной поверхности обычно равно атмосферному (река, водосливные лотки, канализационные трубы). Движение происходит за счет геометрического уклона русла, т.е. под действием силы тяжести.
В гидродинамике движущаяся жидкость рассматривается состоящей из совокупности множества элементарных струек, боковая поверхность которых образована линиями тока. Под линией тока подразумевается линия, касательная к которой в любой точке дает направление вектора скорости в данный момент времени. Следовательно, нормальные составляющие скорости при этом равны нулю, откуда следует отсутствие перетекания жидкости через боковую поверхность данной струйки в соседние с ней. Таким образом, жидкость протекает только через входное и выходное сечения струйки. Такое представление дает возможность использовать для элементарной струйки математический аппарат дифференциального исчисления с последующим интегрированием по сечению всего потока для получения уравнений и закономерностей движения жидкости.
Введем ещё некоторые понятия, используемые в механике жидкости. Так, расходом называется количество жидкости (в объёмных или весовых единицах) протекающей через поперечное сечение в единицу времени, т.е.
,
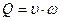где Q - расход,
υ - средняя по сечению скорость,
ω - площадь поперечного сечения потока.
Длина линии поперечного сечения, по которой жидкость соприкасается с твердой границей потока, называется смоченным периметром. Для трубы радиуса r, полностью заполненной жидкостью, смоченный периметр равен
|
|
|
.
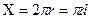Отношение площади сечения ω к смоченному периметру Χ называется гидравлическим радиусом R. Для круглой трубы
.
|
|
|
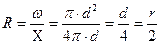