 |
Уравнение Бернулли для элементарной струйки идеальной жидкости (установившееся движение).
|
|
|
|
Уравнение Бернулли является основным уравнением гидравлики, широко используемым в практических приложениях. Для вывода его выделим в движущейся жидкости элементарную струйку (рис.9) и наметим в ней два сечения 1-1 и 2-2.
Площади этих сечений ω1 и ω2, а координаты их центров тяжести z1 и z2. В момент времени t масса жидкости на участке между сечениями 1-1 и 2-2 состояла из отсеков I и Ш. Через время dt эта масса жидкости переместится в новое положение и будет состоять из отсеков Ш и П.
 |
Рис 9
Применим к выделенной массе жидкости теорему механики о том, что приращение кинетической энергии за время dt равно работе внешних сил за тот же промежуток времени. Поскольку отсек Ш не изменяет своего положения, изменение кинетической энергии происходит за счет отсеков I и П, т.е.
.
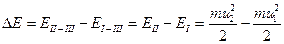У обозначения массы отсеков индексы опущены, так как из уравнения постоянства расхода следует, что массы отсеков I и П равны, т.е.
m1=m2=m=ρqdt.
Тогда
. (8.1)
Из внешних сил работу совершают поверхностные силы гидродинамического давления Р1 и Р2, действующие по торцевым сечениям на выделенный отсек жидкости со стороны отброшенной части потока, и массовые силы, из которых в случае установившегося движения учитываются только силы тяжести.
Работа сил гидродинамического давления:
. (8.2)
Работа силы тяжести состоит из перемещения массы жидкости из отсека I в отсек П, поскольку отсек Ш остается на месте. Следовательно, работу сил тяжести можно записать так:
ρgq(z1-z2)dt. (8.3)
Приравнивая изменение кинетической энергии (8-1) сумме работ внешних сил (8-2) и (8-3), находим:
. (8.4)
Если члены уравнения (8-4) отнести к единице веса протекающей жидкости. т.е. разделить их на ρgqdt (или, что тоже самое на γqdt), то после группировки членов, получим:
|
|
|
,
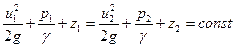или
. (8.5)
В такой форме записи уравнение Бернулли применяется для решения задач движения жидкости по трубам и каналам. Здесь члены уравнения имеют линейную размерность.
Физический смысл уравнения Бернулли заключается в том, что оно представляет собой закон сохранения энергии для частиц жидкости, движущихся вдоль линии тока. Все члены уравнения являются удельными энергиями, т.е. отнесенными к единице веса протекающей жидкости.
Так член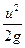 
характеризует удельную кинетическую энергию, член 
- потенциальную энергию давления, а z - потенциальную энергию положения, которая равна высоте расположения частиц над условно выбранной плоскостью сравнения.
Таким образом, анализируя уравнение Бернулли, заключаем, что при движении частицы жидкости по длине элементарной струйки сумма удельных энергий, т.е. полная механическая энергия частицы не изменяется. В этом заключается энергетический смысл уравнения Бернулли.
Члены уравнения Бернулли, записанные в форме (8-5) имеют ещё названия связанные с их линейной размерностью. Так, член 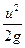называется скоростным напором, член - пьезометрическим напором (высотой), а z - геометрическим напором (высотой). Отсюда следует геометрический смысл уравнения Бернулли, заключающийся в том, что сумма высот скоростного, пьезометрического и геометрического напоров есть величина постоянная. Последние два члена, характеризующие потенциальную энергию, можно для сокращения записи объединить в один, обозначив
.
Тогда уравнение Бернулли (8.5) запишется так:
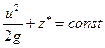. (8.6)
Уравнение Бернулли выведено нами для идеальной жидкости. Для распространения его на поток реальной, т.е. вязкой жидкости необходимо учитывать потери энергии, обусловленные возникновением сил трения. Однако, как показывает опыт, в тех случаях, когда силы трения малы по сравнению с массовыми силами, уравнение Бернулли, полученное для элементарной струйки идеальной жидкости, можно использовать для решения ряда частных задач движения реальной жидкости.
|
|
|
|
|
|
