 |
Обработка результатов прямого измерения
|
|
|
|
Результат многократного измерения, также как и результат однократного измерения, является случайным значением измеряемой величины, но его дисперсия в n раз меньше дисперсии однократного измерения.
Следовательно, точность значения измеряемой величины повышается в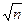 
раз.
При обработке результата измерения с равноточными значениями отсчёта следует выполнять следующие операции:
1. Результат каждого измерения А величины записывается в таблицу.
2. Вычисляется среднее значение из n измерений по формуле:
. (7)
3. Определяется среднеквадратичная ошибка среднего арифметического по формуле:
. (8)
где 
- погрешность отдельного измерения.
Погрешность отдельного измерения определяется по формуле:
. (9)
4. Исключение ошибок по правилу трёх сигм:
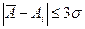. (10)
где σ – значение функции Лапласа при вероятности Р = 0,997.
Значение функции Лапласа определяется из уравнения (приложение А):
. (11)
Если отклонение результата отдельного измерения от среднего арифметического значения больше, чем три сигма, то его считают ошибочным и его отбрасывают, после чего повторяют операции 2, 3, 4.
Если отклонение результата отдельного измерения от среднего арифметического значения меньше, чем три сигма, то проводится проверка нормальности закона распределения вероятности результата измерения.
5. Проверка закона нормальности распределения вероятности результата измерения. Если массив экспериментальных данных n >40…50, то проверка нормальности закона распределения вероятности результата измерения проводится по критерию К Пирсона [4]:
. (12)
Если массив экспериментальных данных n < 40…50, но не больше 10…15, то проверка нормальности закона распределения вероятности результата измерения проводится по составному критерию.
|
|
|
Если же n < 10…15, то проверка нормальности закона распределения вероятности результата измерения не проводится, а гипотеза о нормальности закона распределения вероятности результата измерения принимается или отвергается на основании априорной информации.
6. Определение стандартного отклонения среднего арифметического.
Если распределение вероятности подчиняется нормальному закону, то стандартное отклонение среднего арифметического определяется по формуле:
. (13)
Если же распределение вероятности не подчиняется нормальному закону, то стандартное отклонение среднего арифметического определяется по формуле:
. (14)
7. Выбор доверительной вероятности р и определение параметра К. Если распределение вероятности результата измерения подчиняется нормальному закону, то параметр к определяется по табличным значениям функции Лапласа при заданной доверительной вероятности. Если распределение вероятности результата измерения не подчиняется нормальному закону, то параметр к определяется по табличным значениям неравенства Чебышева.
8. Определяется доверительный интервал (погрешность измерения):
. (15)
9. Если величина погрешности результата измерения δ окажется сравнимой с величиной погрешности прибора δ, то в качестве границы доверительного интервала принимаются:
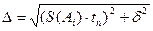. (16)
Если одна из ошибок меньше другой в три или более раз, то меньшую отбрасывают.
10. Окончательный результат запишите в виде
. (17)
11. Оценить относительную погрешность результата измерений:
. (18)
Рассмотрим на числовом примере применение приведенных выше формул.
Пример. Измерялся микрометром диаметр d стержня (систематическая ошибка измерения равна 0.005мм). Результаты измерений заносим во вторую графу таблицы, находим 
и в третью графу этой таблицы записываем разности 
, а в четвертую – их квадраты.
|
|
|
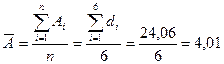мм.
мм.
Таблица 1 – Результаты измерения диаметра стержня
| N | D, мм |
| 
|
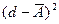
| 4.02 | + 0.01 | 0.0001 | |
| 3.98 | - 0.03 | 0.0009 | |
| 3.97 | - 0.04 | 0.0016 | |
| 4.01 | + 0.00 | 0.0000 | |
| 4.05 | + 0.04 | 0.0016 | |
| 4.03 | + 0.02 | 0.0004 | |
| Σ | 24.06 | – | 0.0046 |
Задавшись надежностью Р = 0,95, по таблице коэффициентов Стьюдента (приложение Б) для шести измерений найдем tn = 2,57. Абсолютная ошибка найдется по формуле:
мм.
Сравним случайную и систематическую ошибки:
.
Следовательно: δ = 0,005 мм можно отбросить.
Окончательный результат запишем в виде
D = (4,01 ± 0,04) мм при Р = 0,95.
.
|
|
|
