Косвенные измерения при нелинейной зависимости

 

При некоррелированных погрешностях измерений a_i используется метод линеаризации путём разложения функции f(а₁,…., а_m) в ряд Тейлора по формуле [4]:

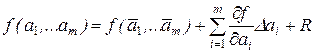, (23)

где Δа_i = a_i - – отклонение отдельного результата наблюдений a_i от ;

R – остаточный член.

Метод линеаризации допустим, если приращение функции f можно заменить её полным дифференциалом. Остаточным членом , пренебрегают, если .

где S(a_i) – оценка среднего квадратического отклонения случайных погрешностей результата измерения a_i.

При этом отклонения Δа_i должны быть взяты из возможных значений погрешностей и такими, чтобы они максимизировали r.

Результат вычислений вычисляют по формуле [4]:

. (24)

Оценку среднего квадратического отклонения случайной составляющей погрешности результата такого косвенного измерения S (A) вычисляют по формуле [4]:

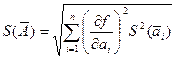, (25)

Значение границ не исключённой систематической погрешности и погрешности Δ (P) результата косвенного измерения при нелинейной зависимости вычисляются так же, как и при линейной зависимости, но с заменой коэффициентов b на .

Метод приведения (для косвенных измерений с нелинейной зависимостью) применяется при неизвестных распределениях погрешностей измерений a_i и при корреляции между погрешностями а_i для получения результата косвенного измерения и определения его погрешности. При этом предполагается наличие рада n результатов наблюдений а_ij измеряемых аргументов a_i. Сочетания а_ij, полученных в j – м эксперименте подставляют в формулу и вычисляют ряд значений А_i измеряемой величины А. Результат измерения а вычисляют по формуле (26) [4].

, (26)

где - доверительная граница случайной погрешности результата измерения;

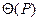- не исключённая систематическая погрешность;

;

;

S (Х) – результат измерения.

, (27)

Оценку среднего квадратического отклонения S (A) случайной составляющей погрешности а вычисляют по формуле [4]:

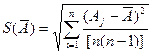, (28)

Границы не исключённой систематической погрешности 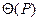и погрешности Δ (P) результата измерения A определяют описанными выше способами для линейной зависимости.

Частными случаями при определении погрешности косвенных измерений при не линейной зависимости можно считать уравнения вида Р = А и Р = А/В для которых значения среднеквадратического отклонения косвенного измерения величины Р можно определить из выражения:

, (29)

где S (A) _A и S (A) _B – средние квадратические отклонения измеряемых аргументов A и B соответственно.

Суммарная погрешность при данных видах нелинейной зависимости искомой величины определяется из выражения:

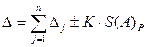, (30)

Пример:

Сопротивление нагрузки определяется по закону Ома R =U/I. Показания вольтметра U = 100 В, амперметра I = 2 А. Средние квадратические отклонения показании: вольтметра S(A)_U = 0,5 В, амперметра S(A) _I = 0,05 А. Доверительные границы истинного значения сопротивления с вероятностью Р = 0,95 (К = l,96) равны...

В данной задаче суммарная погрешность измерения будет определять из уравнения (30) но, так как систематическая погрешность исходя из условия задачи рана нулю уравнение примет следующий вид:

.

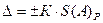Среднеквадратическое отклонение будет определяться из выражения (29):

.

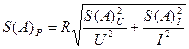В итоге получим, что суммарная погрешность определяется из выражения:

.

В свою очередь доверительные границы определяются из выражения:

,

.

Результат решения задачи следует записать в следующем виде:

при Р = 0,95.

Но не следует забывать, что при не линейной зависимости отличающейся от частных случаев зависимостей, оценка среднего квадратического отклонения проводится в соответствии с уравнением (25) либо (28) в зависимости от вида измерений аргументов а_i и наличия корреляции между ними.

Пример:

Сопротивление R_х измерено с помощью четырехплечего моста и рассчитано по формуле

R_х = R₂ R₄ / R₄.

Найдите относительную среднюю квадратическую погрешность результата измерения, если относительные средние квадратические погрешности сопротивлений R ₂, R ₃ и R ₄ соответственно равны 0,02; 0,01 и 0,01%.

Решение. Относительная средняя квадратическая погрешность сопротивления R_i равна:

S(A)_0i = (S(A) _i / R_i) 100%,

где S(A) _i – средняя квадратическая погрешность сопротивления R_i.

Воспользовавшись формулой среднего квадратического отклонения S(A) случайной погрешности результата косвенного измерения:

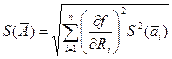
Частная производная берется в точке а₁, а₂, …, а_n, соответствующей результатам прямых измерений, получим:

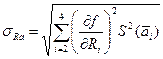
Для данной функции F:

(¶f/¶R ₂)² = (R ₃ / R ₄)² = R ² _х / R ²₂.

Аналогично:

(¶f/¶R ₃)²= R ²_х/ R ²₃,

(¶f / ¶R ₄)² = R ²_х / R ²₄.

Тогда:

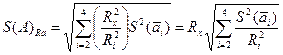
Откуда:

%.

Округление результатов

 

Обработка результатов измерений в лабораториях проводятся на калькуляторах и ПК, и просто удивительно, как магически действует на многих студентов длинных ряд цифр после запятой. «так точнее» – считают они. Однако легко видеть, например, что запись a = 2,8674523 ± 0,076 бессмысленна. При ошибке 0,076 последние пять цифр числа не означает ровно ничего.

Если мы допускаем ошибку в сотых долях, то тысячным, тем более десятитысячным долям веры нет. Грамотная запись результата была бы 2,87 ± 0,08. Всегда нужно производить необходимые округления, чтобы не было ложного впечатления о большей, чем это есть на самом деле, точности результатов.

 

Правила округления

 

1. Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу.

Примеры:

8,27 ≈ 9; 0,237 ≈ 0,3; 0,0862 ≈ 0,09; 0,00035 ≈ 0,0004; 857,3 ≈ 900; 43,5 ≈ 50.

2. Результаты измерения округляют с точностью «до погрешности», т.е. Последняя значащая цифра в результате должна находиться в том же разряде, что и в погрешности.

Примеры:

243,871 ± 0,026 ≈ 243,87 ± 0,03; 243,871 ± 2,6 ≈ 244 ± 3; 1053 ± 47 ≈ 1050 ± 50.

3. Округление результата измерения достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше 5.

Примеры:

8.337 (округлить до десятых) ≈ 8.3; 833.438 (округлить до целых) ≈ 833; 0.27375 (округлить до сотых) ≈ 0.27.

4. Если первая из отбрасываемых цифр больше или равна 5, (а за ней одна или несколько цифр отличны от нуля), то последняя из остающихся цифр увеличивается на единицу.

Примеры:

8,3351 (округлить дл сотых) ≈ 8,34; 0,2510 (округлить до десятых) ≈ 0,3; 271,515 (округлить до целых) ≈ 272.

5. Если отбрасываемая цифра равна 5, а за ней нет значащих цифр (или стоят одни нули), то последнюю оставляемую цифру увеличивают на единицу, когда она нечетная, и оставляют неизменной, когда она четная.

Примеры:

0,875 (округлить до сотых) ≈ 0.88; 0,5450 (округлить до сотых) ≈ 0,54; 275,500 (округлить до целых) ≈ 276; 276,500 (округлить до целых) ≈ 276.

Примечание.

a. Значащими называют верные цифры числа, кроме нулей, стоящих впереди числа. Например: 0,00807 – в этом числе имеется три значащих цифры: 8, ноль между 8 и 7; первые три нуля незначащие. 8.12 · 10³ – в этом числе 3 значащих цифры.

b. Записи 15,2 и 15,200 различны. Запись 15,200 означает, что верны сотые и тысячные доли. В записи 15,2 – верны целые и десятые доли.

c. Результаты физических экспериментов записывают только значащими цифрами. Запятую ставят сразу после отличной от нуля цифры, а число умножают на десять в соответствующей степени. Нули, стоящие в начале или конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записывают так: 4,35·10^-3 и 2,34·10⁵. Подобная запись упрощает вычисления, особенно в случае формул, удобных для логарифмирования.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: