Средняя скорость переменного движения

 

,

 

где - длина участка траектории, - продолжительность промежутка времени.

Модуль вектора скорости переменного движения

,

 

где - путь, проходимый точкой за время .

Закон сложения скоростей в классической механике

 

,

где - скорость тела относительно некоторой системы отсчета К₁,

- скорость системы К₁ относительно другой системы К₂.

Мгновенное ускорение

 

 

Модуль перемещения при равномерном прямолинейном движении

 

,

 

где 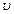- скорость тела, - время движения.

Уравнение равноускоренного прямолинейного движения

 

,

 

где - скорость тела в начальный момент времени.

Скорость при равноускоренном прямолинейном движении

 

 

Модуль перемещения при равноускоренном прямолинейном движении

 

 

Связь линейной и угловой скорости

 

,

 

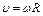где -радиус круговой траектории.

Центростремительное ускорение

 

 

Период вращения тела

 

 

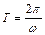
Плотность однородного тела

,

 

где - масса тела, - объем тела.

Импульс тела

,

 

где - масса тела, - скорость движения тела.

Закон сохранения импульса

 

,

 

где - массы соударяющихся тел, - скорости тел до соударения, 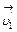, 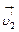- скорости тел после соударения.

Сила трения

,

 

где - коэффициент трения, - сила нормальной реакции опоры.

Сила упругости (закон Гука для пружины)

 

,

 

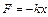где 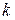- коэффициент жесткости пружины, - растяжение или сжатие пружины.

Сила тяжести

 

,

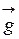- ускорение свободного падения.

Закон всемирного тяготения

 

,

 

где - гравитационная постоянная, 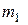и - массы тел, - расстояние между телами.

Ускорение свободного падения на планете

,

 

где G- гравитационная постоянная,

М – масса планеты,

R – радиус планеты.

Второй закон Ньютона

 

,

 

где - масса тела, - ускорение тела, - равнодействующая всех сил, действующих на тело.

Третий закон Ньютона

,

 

где - сила, действующая на первое тело со стороны второго, - на второе со стороны первого.

Импульс силы

 

,

 

где - импульса тела за время .

Работа в случае постоянной силы

 

,

 

где - угол между направлением действия силы и направлением перемещения.

Средняя мощность

 

,

 

где - работа, совершенная за промежуток времени .

Кинетическая энергия тела

.

 

Потенциальная энергия тела в поле силы тяжести

 

,

 

где 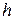- высота, - ускорение свободного падения.

Потенциальная энергия деформированной пружины

 

,

 

где - коэффициент жесткости пружины, - величина деформации пружины.

Коэффициент полезного действия

 

или ,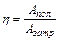

 

где - полезно используемая энергия,

Е – подводимая энергия,

- полезная работа,

- затраченная (полная) работа.

Момент силы

 

,

 

где - плечо силы (расстояние от центра вращения до линии действия силы).

Условия равновесия тела

 

,

 

 

где - силы, действующие на тело, - моменты сил, действующих на тело.

Релятивистское сок­ращение длины стержня

Релятивистское замедление хода часов

Релятивистское сложение скоростей

Релятивистский импульс ,
Полная энергия релятивистской частицы

Релятивистское выражение для кинетической энергии: .

 

Отсюда следует, что является энергией покоя.

Полная энергия и импульс частицы связаны соотношением: .

Масса частицы есть инвариантная величина, которая определяется из следующего выражения: .

 

Уравнение гармонических колебаний

,

 

где х – смещение тока от положения равновесия,

x_m – амплитуда колебаний,

- фаза колебаний,

- циклическая частота,

t – время,

- начальная фаза.

Связь частоты колебаний и периода

,

 

где - циклическая частота.

Период колебаний и циклическая частота математического маятника

,

 

где l – длина маятника, g – ускорение свободного падения.

Уравнение движения пружинного маятника имеет вид:

, или .

 

Период колебаний и циклическая частота пружинного маятника

,

где m – масса груза, k – коэффициент жесткости пружины.

При малых амплитудах колебания уравнение движения физического маятника имеет вид: или .

Период колебаний и циклическая частота физического маятника

,

Приведенная длина физического маятника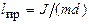

Примеры решения задач.

Задача 1. Свободно падающее тело прошло последние 10 м за 0,25 с. Определите высоту падения и скорость в момент падения.

 

Дано:

Решение:

Высота падения 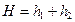. Расстояние h₁ можно найти из уравнения , - скорость тела в точке А. Эта скорость является начальной при прохождении телом отрезка пути h₂, поэтому ее можно найти из соотношения

 

Отсюда

.

 

Здесь оказывается удобным рассчитать величину :

 

 

(ускорение свободного падения принимаем равным 10 м/с²).

Расстояние найдем с помощью формулы

 

 

 

Высота падения тела Н=76+10=86 м.

Скорость в момент падения

 

,

 

.

 

Задача 2. Линейная скорость точек окружности вращающегося диска равна 3 м/с, а точек, находящихся на 10 см ближе к оси вращения, - 2 м/с. Сколько оборотов сделает диск в секунду?

 

Дано:

 

Решение

Обозначим расстояние от точек, имеющих скорость 3 м/с, до оси вращения через R, тогда расстояние от точек, имеющих скорость 2 м/с, до оси будет равно R-l. Используя формулу связи линейной скорости с числом n оборотов в секунду, для этих точек можно записать:

 

(1)

 

(2)

 

Число п одинаково для всех точек диска. Поделив уравнение (2) на (1), получим

,

 

откуда

 

Задача 3. Определите ускорение тела, соскальзывающего с наклонной плоскости 30⁰, а коэффициент трения между телом и наклонной плоскостью 0,3.

Дано:

 

Решение

На тело действуют три силы, изображенные на рисунке. направим ось х вдоль наклонной плоскости в сторону движения тела, а ось у – перпендикулярно наклонной плоскости в сторону действия силы N. Сумма проекций сил на ось х равна . По второму закону Ньютона

 

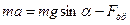(1)

 

Так как движение тела в этом направлении не происходит, то сумма проекций сил на ось у равна нулю,, т.е.

 

.

 

a

Из последнего соотношения

 

.

 

Сила трения равна

 

 

Ускорение тела найдем из уравнения (1):

 

 

 

 

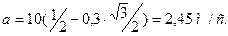
Задача 4. На невесомом стержне висит груз массой m. Груз отклоняют так, что стержень занимает горизонтальное положение, и отпускают. Найдите натяжение стержня при прохождении грузом положения равновесия.

 

Решение

На груз в нижней точке траектории действуют две силы: сила натяжения и сила тяжести . Равнодействующая этих сил создает центростремительное ускорение

 

,

 

где - скорость, с которой груз проходит положение равновесия, R – радиус траектории (в данном случае длина стержня).

По второму закону Ньютона

 

 

.

 

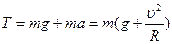По закону сохранения энергии кинетическая энергия груза, которой он обладает при прохождении положения равновесия, равна потенциальной энергии в отклоненном положении:

 

,

 

где .

Отсюда

.

 

Подставив это выражение в формулу для Т, получим

 

.

 

Задача 5. Тело массой 2 кг, падающее с высоты 5 м, проникает в мягкий грунт на глубину 5 см. Определите среднюю силу сопротивления грунта.

 

Дано:

 

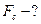
Решение

 

Будем считать, что потенциальная энергия тела в точке В равна нулю. Тогда в точке С тело обладает потенциальной энергией . При падении тела его скорость возрастает и

у поверхности земли будет равна . Тогда полная механическая энергия тела на поверхности земли равна . За счет этой энергии на участке ВО совершается работа, равная . Таким образом

 

. (1)

 

Из закона сохранения механической энергии на участке ВО имеем

 

. (2)

 

Подставляя формулу (2) в уравнение (1), получим

 

 

откуда

 

.

 

Задача 6. Насос заполняет водой бассейн за 20 мин. Найдите мощность двигателя насоса, если его центр находится на высоте 18 м над поверхностью воды в озере, а КПД насоса 90%. Емкость бассейна 100 м³.

 

Дано:

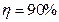
(1)

 

Решение

Если в условии задачи известен КПД, то решение задачи удобно начинать с него. В данном случае

 

,

 

где – полезная работа, которая идет на подъем тела, - полная работа двигателя насоса.

Полезная работа равна

 

.

 

Затраченную работу можно выразить через мощность насоса

 

.

 

Подставив полученные выражения в формулу (1). Получим

 

.

 

Откуда

 

 

Задача 7. Определите плотность однородного тела, вес которого в воздухе 2,8 Н, а в воде 1,69 Н. Выталкивающей силой воздуха пренебречь.

 

Дано:

 

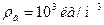
Решение

Если пренебречь выталкивающей силой воздуха, то вес тела в воде будет меньше веса в воздухе на величину выталкивающей силы в воде:

 

 

Поскольку 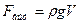, где - плотность воды, V – объем тела, то

 

. (1)

 

Объем тела равен частному от деления массы тела на плотность вещества, из которого оно изготовлено: . Массу m выразим через вес Р: , тогда . Подставив выражение для V в уравнение (1), получим

 

.

 

Отсюда

.

 

кг/м³

Задача 8. Под действием горизонтальной силы F брусок массой m движется по столу с некоторым ускорением. Если силу увеличить в п раз, то ускорение бруска увеличится в k раз. Определить коэффициент трения бруска о стол.

 

Решение

Второй закон Ньютона для движущегося бруска запишется в виде

 

, (1)

 

где F_тр – сила трения, а – ускорение бруска.

После увеличения силы второй закон Ньютона принимает вид

 

. (2)

 

Разделив (2) на (1) получим

 

.

 

После приведения к общему знаменателю имеем

 

,

 

откуда

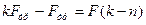. (3)

 

Для бруска, движущегося по горизонтальному столу

 

, (4)

 

где - коэффициент трения.

После подстановки (4) в (3) получаем

 

.

 

Задача 9. Однородный стержень с прикрепленным на одном из его концов грузом массой 1,2 кг находится в равновесии в горизонтальном положении, если его подпереть на расстоянии 1/5 длины стержня от груза. Чему равна масса стержня?

 

Дано:

Решение

Силы, действующие на стержень, показаны на рисунке.

Сила стремится вращать стержень вокруг оси, проходящей через точку О против часовой стрелки, ее момент равен

 

.

 

Сила 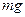стремится вращать стержень по часовой стрелке, ее момент равен

 

.

 

По правилу моментов стержень находится в горизонтальном положении, если

 

 

 

Обозначим длину стержня через l, тогда

 

.

 

После подстановки

 

,

 

откуда

.

 

 

Задача 10. За какое время маятник отклоняется от положения равновесия на половину амплитуды, если период колебания 3,6 с?

 

Дано:

(1)

 

Решение

Время t отклонения маятника от положения равновесия входит в уравнение колебаний

 

,

где х – смещение маятника, x_m – амплитуда, - циклическая частота.

Из формулы (1)

 

.

 

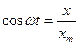Используя данные задачи, получим

 

.

 

Откуда

.

 

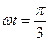Так как

,

 

то

,

 

откуда

.

 

Задача 11. Часы, период колебаний маятника которых 1 с (часы с секундным маятником), на поверхности Земли идут плохо. На сколько будут отставать эти часы за сутки, если их поднять на высоту 200 м над поверхностью Земли?

 

Дано:

 

 

Решение

Обозначим период колебаний маятника, поднятого над Землей, за . Тогда за одно колебание часы отстанут на (Т₂-Т₁). Для нахождения нужно разность (Т₂-Т₁) умножить на число колебаний N, которое совершает на Земле за сутки

секундный маятник.

 

(1)

 

Число колебаний равно

 

. (2)

 

Период колебаний математического маятника определяется по формуле

 

,

 

где - ускорение свободного падения на Земле.

Тогда

,

 

где - ускорение свободного падения на высоте h.

Отсюда периоды относятся как

 

. (3)

 

Из сравнения силы притяжения двух тел и силы тяжести получается выражение для ускорения свободного падения:

 

, (4)

 

где - гравитационная постоянная, - масса Земли, - расстояние от тела до центра Земли.

В соответствии с формулой (4)

 

. (5)

 

Подставив (5) в (3), получим

 

,

 

откуда

. (6)

 

После подстановки (6) и (2) в (1) имеем

 

.

 

Задача 12. В брусок массой М, лежащий на гладком столе и прикрепленный к горизонтальной пружине, соединенной со стенкой, попадает пуля массой m, летящая вдоль стола со скоростью . Чему будет равна амплитуда колебаний бруска с застрявшей в нем пулей, если жесткость пружины равна ?

 

Решение

 

 

Скорость , которую сообщит телу пуля, определяется с помощью закона сохранения импульса:

 

,

 

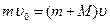откуда

.

 

Кинетическая энергия тела с пулей полностью переходит в потенциальную энергию пружины, сжатой на максимальную величину . Отсюда

 

.

 

После подстановки

 

,

 

откуда амплитуда колебаний пружины равна

 

.

 

Задача 13. При подвешивании груза массой 1 кг стальная пружина в положении равновесия удлинилась на 1 см. С каким периодом будет совершать колебания этот груз напружине после смещения его по вертикали от положения равновесия?

 

 

Дано:

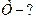
(1)

 

Решение

Период колебаний пружинного маятника можно найти с помощью формулы

 

,

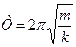где k – жесткость пружины.

Жесткость пружины можно найти по ее удлинению под действием силы тяжести груза массы m. Для модуля силы упругости в положении равновесия выполняется равенство

 

,

 

откуда

.

 

Подставив полученное выражение в формулу (1), получим

 

 

.

 

 

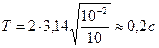⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: