 |
Модуль 3. Электричество и магнетизм
|
|
|
|
Основные формулы
Закон Кулона
,
где F – модуль силы взаимодействия зарядов q1 и q2,
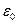- электрическая постоянная,
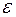- диэлектрическая проницаемость среды,
r – расстояние между телами.
Закон сохранения электрического заряда
,
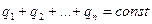где слева записана алгебраическая сумма зарядов всех тел в замкнутой системе.
Напряженность электрического поля
,
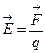где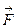 
- электрическая сила, действующая на заряд, q – величина заряда.
Сила, действующая на заряд в электрическом поле
.
Напряженность поля точечного заряда
.
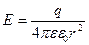Принцип суперпозиции определяет напряженность электрического поля
,
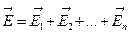где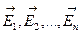 
- векторы напряженности полей, созданных несколькими зарядами в данной точке.
Поверхностная плотность заряда
,
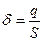где S – площадь поверхности.
Потенциал электростатического поля
,
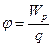где Wp – потенциальная энергия заряда q в электрическом поле.
Потенциал поля точечного заряда или заряженной сферы
.
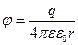Принцип суперпозиции полей для потенциалов
,
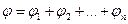где справа записана алгебраическая сумма потенциалов, созданных каждым зарядом в данной точке.
Связь между напряженностью Е и разностью потенциалов U между двумя токами в однородном электрическом поле
,
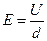где d – расстояние между двумя точками.
Работа перемещения заряда в электрическом поле
,
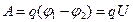где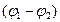 
- разность потенциалов двух точек поля.
Электрическая емкость конденсатора
,
где q – заряд на одной из обкладок конденсатора, U – напряжение между обкладками.
Емкость плоского конденсатора
,
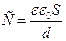где S – площадь обкладок конденсатора, d – расстояние между обкладками.
Емкость батареи параллельно соединенных конденсаторов
|
|
|
.
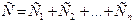Емкость батареи, состоящей последовательно соединенных конденсаторов
.
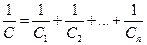Энергия заряженного конденсатора
.
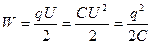Объемная плотность энергии электрического поля напряженности Е
Сила тока
,
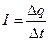где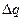 
- заряд, протекающий через поперечное сечение проводника за время 
.
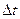Закон Ома для участка цепи
,
где U – напряжение на данном участке цепи, R – сопротивление участка.
Сопротивление однородного проводника
,
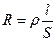где 
- удельное сопротивление материала проводника, l – длина проводника, S – площадь поперечного сечения проводника.
Сопротивление цепи, состоящей из последовательно соединенных проводников
.
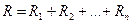Сопротивление цепи, состоящей из параллельно соединенных проводников
.
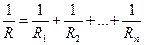Работа тока
.
.
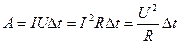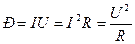Закон Ома для замкнутой цепи
,
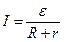где 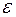- электродвижущая сила (ЭДС) источника,
R – сопротивление внешнего участка цепи, r – сопротивление внутреннего участка цепи.
Закон Фарадея для электролиза
,
где m – масса выделившегося на электроде вещества, I – сила тока, 
- время протекания тока, k – электролитический эквивалент вещества.
Сила, действующая на проводник с током в магнитном поле (сила Ампера)
,
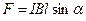где I – сила тока, текущего по проводнику, В – индукция магнитного поля, l – длина проводника, 
- угол между вектором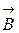 
и направлением тока.
Сила, действующая на электрический заряд, движущийся в магнитном поле (сила Лоренца)
,
где q – величина заряда, 
- скорость движения заряда, 
- угол между вектором 
и направлением движения заряда.
Электродвижущая сила индукции (ЭДС)
,
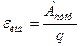где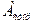 
- работа сторонних сил по перемещению заряда q.
Магнитный поток, пронизывающий контур площади S
,
где - угол между вектором и нормалью к плоскости контура.
Основной закон электромагнитной индукции
,
|
|
|
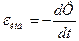где 
- электродвижущая сила, возникающая в контуре,
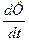- скорость изменения магнитного потока, пронизывающего контур.
Связь между магнитным потоком и силой тока в контуре
,
где L – индуктивность контура.
ЭДС самоиндукции
,
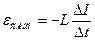где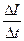 
- скорость изменения силы тока в контуре.
Энергия магнитного поля проводника с током
,
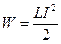где L – индуктивность проводника, I – сила тока в проводнике.
Период электромагнитных колебаний
,
где L – индуктивность катушки, С – емкость конденсатора.
Действительное значение напряжения и силы тока
, 
,
где 
и 
- амплитудное значение напряжения и силы тока соответственно.
Индуктивное сопротивление
,
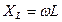где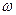 
- циклическая частота колебаний, L – индуктивность катушки.
Емкостное сопротивление
,
где 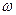- циклическая частота колебаний, С – емкость конденсатора.
Условие резонанса
,
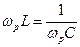где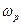 
- резонансная частота, L – индуктивность катушки, С – емкость конденсатора.
Скорость распространения волны
,
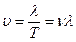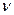- частота, 
- длина волны.
Примеры решения задач
Задача 1. Два шарика массой по 0,2 г подвешены на тонких шелковых нитях длиной 0,5 м так, что поверхности их соприкасаются. После того, как шарики были заряжены одинаковыми по величине электрическими зарядами, они оттолкнулись друг от друга и разошлись на расстояние 5 см между центрами. Определите величину заряда каждого шарика.
 Дано:
 
|
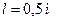
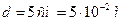
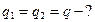
Когда шарики разойдутся, на каждый из них будут действовать три силы: сила тяжести mg, кулоновская сила Fэл и сила натяжения нити Т. Поскольку каждый шарик находится в состоянии равновесия, то равнодействующая всех сил равна нулю. Направим ось х горизонтально, а ось у - вертикально, как показано на рисунке. Алгебраические суммы проекций сил на эти оси равны нулю. Поэтому можно записать
.
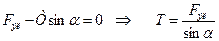
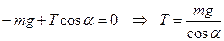Из последних соотношений получаем
.
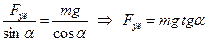По закону Кулона 
.
Тогда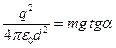 
. Угол мал, поэтому можно предположить, что 
. В итоге
.
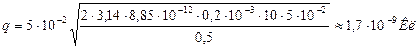
Задача 2. Электрон вылетает из точки, потенциал которой равен 6000 В, имея скорость, направленную вдоль поля и равную 3.107 м/с. Определите потенциал точки, в которой скорость электрона станет равной нулю.
Дано:
|
|
|
|
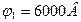
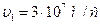
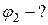
Решение
При движении электрон за счет своей кинетической энергии совершает работу против сил поля, численно равную 
. Поэтому
или, учитывая, что
.
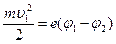Отсюда
.
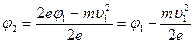
Задача 3. Амперметр измеряет ток до 0,025 А, его сопротивление 3 Ом. Какой длины нужно взять манганиновую проволоку диаметром 1 мм для изготовления шунта, чтобы амперметр мог измерять ток до 2,5 А?
Дано:
 
|
. |
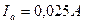
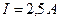
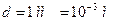
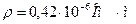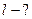
Решение
Соединение шунта с амперметром показано на рисунке
По закону параллельного соединения
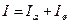, (1)
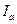- сила тока, протекающего через амперметр, 
- сила тока, текущая через шунт.
Отсюда
.
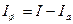Напряжения на шунте и амперметре одинаковы (параллельное соединение) и равны
,
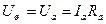где Ra – сопротивление амперметра.
Поскольку
,
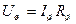где Rш – сопротивление шунта, то
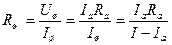. (2)
Длина проволоки, из которой изготовлен шунт, связана с его сопротивлением формулой
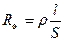, (3)
где - удельное сопротивление манганина,
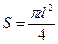- площадь поперечного сечения проволоки, где d - диаметр проволоки.
Приравняем правые части выражений (2) и (3)
.
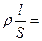
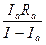Отсюда
.
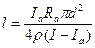
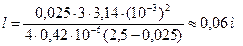
Задача 4. Определите сопротивление раствора серной кислоты, если известно, что при прохождении тока за 2 часа выделяется 0,72 г водорода. Мощность, затраченная на нагревание электролита, равна 100 Вт.
Дано:
 
|
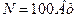
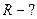
Решение
Сопротивление входит в формулу мощности
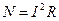
Откуда
.
Силу тока можем определить, используя закон Фарадея для электролиза:
,
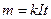откуда
Тогда
.
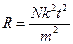
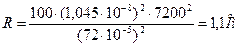Задача 5. На прямолинейный нихромовый проводник площадью поперечного сечения 1 мм2, помещенный в однородное магнитное поле с индукцией 0,4 Тл, действует сила 0,5 Н. Угол между проводником и направлением линий индукции магнитного поля составляет 300. Определите падение напряжения на проводнике.
Дано:
 
|
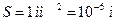
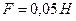
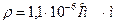
Решение
На проводник с током, помещенный в магнитное поле, действует сила Ампера
.
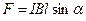Падение напряжения на проводнике равно
|
|
|
.
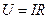Поскольку сопротивление проводника равно
,
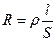то после подстановки получаем
Силу тока можно найти, используя закон Ампера
,
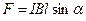где В – индукция магнитного поля.
Отсюда
.
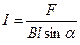Подставив это значение в выражение для напряжения, получим
.
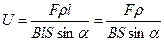
Задача 6. Электрон, ускоренный разностью потенциалов 2000 В, влетает в однородное магнитное поле с индукцией 15.10-4 Тл перпендикулярно линиям индукции и движется по окружности. Определите радиус окружности.
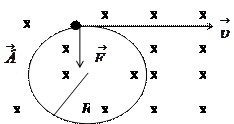
Дано:
|
|
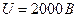
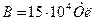
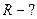
Пусть магнитное поле направлено от нас. На влетевший в это поле электрон действует сила Лоренца. Направление этой силы определяем по правиле левой руки. Модуль силы Лоренца
,
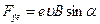где - скорость электрона, - угол между 
и В. В нашем случае 
, поэтому
.
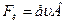Запишем для электрона второй закон Ньютона в скалярной форме относительно оси у:
,
где m – масса электрона,
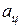- центростремительное ускорение, равное 
.
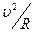Тогда
.
Откуда
.
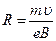Электрон, ускоряясь в электрическом поле, приобретает кинетическую энергию за счет работы сил электрического поля. Поэтому
.
Подставив полученное выражение для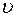 
в предыдущую формулу, получим
,
.
Задача 7. Индуктивность катушки равна0,08 Гн, действующее значение напряжения 100 В, частота тока 100 Гц. Определите амплитуду тока в цепи. Активным сопротивлением катушки и подводящих проводов пренебречь.
Дано:
 
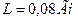
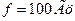
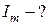
| (1) |
Решение
Амплитудное значение силы тока определяется по формуле
,
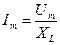где – амплитудное значение напряжения,
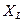- индуктивное сопротивление катушки.
связано с действующим значением напряжения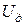 
соотношением
,
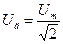откуда
.
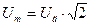Индуктивное сопротивление равно
,
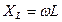где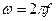 
- циклическая частота.
После подстановки в (1) имеем
.
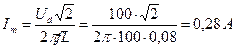Задача 8. На какую длину волны настроен колебательный контур, если он состоит из катушки, индуктивность которой 2.103 Гн, и плоского конденсатора? Расстояние между пластинами конденсатора 1 см, диэлектрическая проницаемость вещества, заполняющего пространство между пластинами, равна 11, площадь пластины 800 см2.
Дано:
 
|
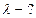
Решение
Длина волны, на которую настроен контур, связана с периодом электромагнитных колебаний Т соотношением 
, где с – скорость распространения электромагнитных волн (света) в вакууме, равная 3.108 м/с. Период колебаний контура найдем по формуле Томсона
,
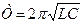где С – емкость контура, равная 
.
Тогда
.
Подставив эту формулу в выражение для 
, получим
|
|
|
,
.
|
|
|
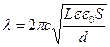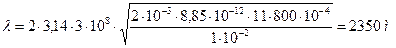