 |
Модуль 2. Термодинамика и молекулярная физика.
|
|
|
|
Основные формулы
Основное уравнение молекулярно-кинетической теории
,
где 
- масса одной молекулы, 
- концентрация молекул (количество молекул 
, отнесенное к объему 
, в котором он находится), 
- квадрат средней квадратичной скорости.
Средняя кинетическая энергия поступательного движения молекулы идеального газа
,
где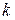 
- постоянная Больцмана, 
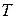- абсолютная температура газа.
Масса молекулы
,
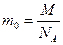где 
- молярная масса, NA- число Авогадро.
Количество вещества
,
где m - масса, N- количество молекул.
Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
,
где p - давление газа, V - объем, занимаемый газом, R- универсальная газовая постоянная.
Закон Дальтона
,
где р - давление смеси газов, р1, р2,…,рn - парциальные давления (давления, производимые каждым газом, если бы он один занимал весь объем).
Внутренняя энергия одноатомного газа
Работа изобарического расширения газа от объема V1 до объема V2
,
где р - давление газа.
Количество теплоты, необходимое для нагревания тела
,
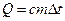где с – удельная теплоемкость вещества, m – масса тела, 
- изменение температуры тела.
Количество теплоты, необходимое для плавления тела
,
где 
- удельная теплота плавления, m- масса тела.
Количество теплоты, необходимое для испарения тела
,
где r - удельная теплота парообразования.
Уравнение теплового баланса
,
где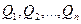 
- теплота, отданная в результате теплообмена,
- теплота, полученная при теплообмене.
Первый закон термодинамики
,
где Q - количество теплоты, полученной телом, 
- изменение внутренней энергии тела, А – работа, совершаемая телом против внешних сил.
|
|
|
КПД теплового двигателя
,
где Q1 – теплота, полученная от нагревателя, Q2 – теплота, отданная холодильнику.
КПД идеального теплового двигателя
,
где Т1 – температура нагревателя, Т2 – температура холодильника.
Относительная влажность воздуха
,
где р – давление паров воды, рнас – давление насыщенных паров воды при данной температуре.
Примеры решения задач
Задача 1. В цилиндре с площадью основания 0,1 м2 под поршнем находится 5 л воздуха. Давление снаружи 1 атм. На сколько опустится поршень, если на него положить груз массой 49 кг? Массу поршня и трение его о стенки цилиндра не учитывать. Процесс считать изотермическим.
Дано:
 
|
Решение
При опускании поршня объем газа изменится на 
, где V2 – конечный объем. Тогда расстояние h, на которое опустится поршень, можно определить из соотношения
Для нахождения V2 воспользуемся законом Бойля-Мариотта.
,
Откуда
Давление р2 связано с первоначальным выражением
Подставив последнее соотношение в предыдущую формулу, получим
.
Искомое соотношение будет иметь вид
.
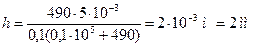Задача 2. В сосуде находится 0,5 кг воды при 00С. Какое количество водяного пара при 1000С было впущено в воду, если температура воды стала 300С? Теплоемкость сосуда не учитывать. удельная теплоемкость воды 4,2.103 Дж/(кг.град). удельная теплота парообразования 22,6.105 Дж/кг.
Дано:
 
 
|
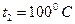
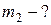
Решение
Пар, попадая в холодную воду, конденсируется. При этом выделяется теплота конденсации 
. Стоградусный конденсат, остывая до 300С, отдает количество тепла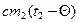 
. В результате вода, находящаяся в сосуде, нагревается до 300С, принимая теплоту 
.
Составим уравнение теплового баланса:
.
Решая уравнение, получаем
Задача 3. Один моль газа, имевший начальную температуру Т, при постоянном давлении расширился, совершив работу А. во сколько раз при этом увеличился объем газа?
|
|
|
Дано:
 
| (1) |
Решение
Работа при изобарическом расширении газа определяется по формуле
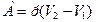
Выразив V1 и V2 с помощью уравнения состояния
и подставив V1 и V2 в соотношение (1), получим
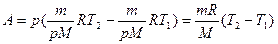. (2)
Для изобарического процесса справедливо равенство отношений
.
Разность температур из (2) равна
. (4)
Разделим левую и правую части выражения (4) на Т1:
,
откуда
.
Таким образом, отношение объемов газа в соответствии с (3) равно
.
Задача 4. Бронзовая статуэтка весит в воздухе 21,1 Н, а в воде 11,3 Н. Каков объем воздушной полости статуэтки?
Дано:
 
|
Решение
Объем полости можно найти, вычитая из объема статуэтки V объем бронзы Vбр:
(1)
Объем бронзы входит в выражение для веса тела в воздухе:
,
откуда
. (2)
Вес тела в воде Р2 определяется из соотношения
,
откуда
. (3)
Подставив (3) и (2) в (1), получим
.
Задача 4. Сравните число атомов, из которых состоят серебряная и алюминиевая ложки равного объема. Плотность и атомная масса серебра соответственно 10,5.103 кг/м3 и 108.10-3 кг/моль; для алюминия 2,7.103 кг/м3 и 27.10-3 кг/моль.
Дано:
|
Решение
Число атомов, содержащихся в твердом теле равно произведению числа Авогадро на количество вещества:
,
где m – масса тела, М – атомная масса.
Известно, что 
, где 
- плотность вещества, V – объем тела. Тогда
(1)
В соответствии с формулой (1) число атомов алюминия
,
серебра
.
С учетом этого
.
Ответ: число атомов примерно одинаково.
|
|
|
