Теоремы о взаимосвязи опорных решений и угловых точек области допустимых решений

Теорема 3. Любое опорное решение является точкой области допустимых решений.

Доказательство. Пусть Х= (х ₁₀, х ₂₀ , …, х_т0 , 0, …, 0)—опорное решение с базисом Б = (A ₁, А ₂,..., А_т )некоторой задачи с системой ограничений А ₁ х ₁ +А ₂ х ₂ +...+ А_п х_п=А₀. Предположим, что X не является угловой точкой, тогда решение представляет собой выпуклую линейную комбинацию каких-либо точек области допустимых решений, не совпадающих с X, например X' и X", т.е. Х=λ ₁ Х'+λ ₂ Х", λ ₁> 0, λ ₂> 0, λ ₁ +λ ₂ = 1.

Так как последние п - т координат вектора X равны нулю, а λ ₁и λ ₂положительные, то последние п-т координат векторов X' и X" также равны нулю, т.е. Х'= (х' ₁, х' ₂,..., х'_т, 0,.., 0) и Х"= (х" ₁, х" ₂,..., х"_т, 0,.., 0).

Подставим X', X" в систему ограничений:

А ₁ х´ ₁ + А ₂ х´ ₂ +... + А_т х_т´ = А₀ ,

А ₁ х´´ ₁ + А ₂ х´´ ₂ +... + А_т х_т´´= А₀ .

Вычтем из первого равенства второе. Получим

А ₁ (х´ ₁ - х´´ ₁) + А ₂ (х´ ₂ - х´´ ₂) +... + А_т (х_т´- х_т´´)= θ.

Так как векторы А ₁, А ₂,..., А_т образуют базис, то они линейно независимы, а потому данное равенство может выполняться только тогда, когда все коэффициенты при векторах равны нулю, т.е. х´ ₁- х´´ ₁=0, х´ ₂- х´´ ₂=0,..., х_т´- х_т´´= 0.

Отсюда получаем, что х´ ₁ = х´´ ₁, х´ ₂ = х´´ ₂,..., х_т´= х_т´´. Следовательно, X' = X" и опорное решение X является не выпуклой линейной комбинацией каких-либо точек области допустимых решений, а угловой точкой этой области.

Теорема 4. Любая угловая точка области допустимых решений является опорным решением.

Доказательство. Пусть Х= (х ₁, х ₂,..., х_т, 0,..., 0) угловая точка области допустимых решений, а х_j > 0 для любого j = 1, 2,..., т. Чтобы доказать, что это решение является опорным, достаточно показать, что векторы А ₁, А ₂ ,..., А_т , соответствующие положительным координатам решения, линейно независимы.

Предположим, что эти векторы линейно зависимы. Тогда существует ненулевой набор чисел l ₁, l ₂,..., l _m, такой, что А ₁ l ₁ + А ₂ l ₂ +... + A _m l_m =θ. (3.1)

Так как X ― допустимое решение, то А ₁ х ₁ + А ₂ х ₂ +... + А_п х_п = А₀ . (3.2)

Умножим соотношение (3.1) на некоторое число ε и прибавим к равенству (3.2), получим А ₁ (х ₁ + l ₁ ε) + А ₂ (х ₂+ l ₂ ε) +... + А_т (х_т+ l _m ε) = А₀ , вектор Х '= (х ₁ + l ₁ ε, х ₂+ l ₂ ε, …, х_т+ l _mε, 0,…,0) является решением системы ограничений задачи. Аналогично можно показать, что решением системы является также вектор X" =(х ₁ - l ₁ ε, х ₂ - l ₂ ε, …, х_т- l _m ε, 0,..., 0).

Для того чтобы векторы X ´ и X" удовлетворяли условиям неотрицательности, выберем достаточно малое число ε так, что х _j ± l _j ε > 0 при любых j. Эго возможно, так как х _j > 0 при любых j = 1, 2,..., т. При таком выборе числа ε векторы X' и X" являются допустимыми решениями. Нетрудно видеть, что X = = , т.е. X представляет собой выпуклую линейную комбинацию X' и X". Это противоречит тому, что Х является угловой точкой. Следовательно, векторы А ₁, А ₂ ,..., А _т линейно независимы и решение Х является опорным.

Симплексный метод решения задач линейного программирования

Симплекс-метод

Симплексный метод — это метод целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчета либо найти оптимальное решение, либо установить, что оптимального решения не существует.

Идея симплексного метода состоит в следующем. Используя систему ограничений, приведенную к общему виду, т. е. к системе т линейных уравнений с п переменными (т < п), находят ее любое базисное решение, по возможности наиболее простое. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то переходят к другому допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении линейная форма если и не достигнет оптимума, то приблизится к нему (в случае перехода к вырожденному базисному решению значение линейной формы не изменится). С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.

Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляют переход к другим базисным решениям, которые позволяют приблизиться к области допустимых решений, пока на каком-то шаге не получится допустимое базисное решение. После этого к нему применяют механизм симплексного метода, изложенный выше.

Метод называется симплексным, так как области допустимых решений задач, которые рассматривались на начальном этапе развития метода, имели простейший (simple) вид.

Задача 4. Для изготовления шкафов и буфетов деревоотделочный завод применяет древесину четырех видов. Запасы древесины по каждому виду ограничены и составляют соответственно 120, 160, 120, 80 ед. Количество единиц древесины каждого вида, необходимое для изготовления одного шкафа и одного буфета, а также прибыль, получаемая заводом от реализации единицы продукции, даны в таблице 9.

Требуется составить такой план выпуска продукции, который бы обеспечил предприятию наибольшую прибыль от реализации всей продукции.

Решение. Дадим математическую формулировку задачи. Пусть х ₁и х ₂— количество шкафов и буфетов, запланированныхк производству.

Так как количество древесины по каждому виду ограничено, то должны выполняться следующие неравенства:

Таблица 9 – Исходные данные задачи.

 

Эта система неравенств и является системой ограничений данной задачи. Целевая функция (линейная форма), выражающая прибыль предприятия, имеет вид F = 2 х ₁+ 3 х ₂.

Итак, задача сводится к нахождению максимума функции

F = 2 х ₁+ 3 х ₂ при ограничениях

Для сведения системы ограничений-неравенств к системе уравнений прибавим к левой части каждого неравенства добавочные неотрицательные переменные х _3, х ₄, х ₅, х ₆. В условиях данной задачи они имеют конкретное экономическое содержание, а именно выражают объем остатков древесины каждого вида после выполнения плана по выпуску продукции. После введения добавочных переменных получим систему уравнений

(8)

Нужно найти такое допустимое базисное решение этой системы ограничений, которое бы максимизировало линейную форму F = 2 х ₁+ 3 х ₂ .

Так как система ограничений есть система четырех независимых уравнений с шестью переменными, то число базисных переменных должно равняться четырем, а число свободных — двум.

Для решения задачи симплексным методом прежде всего нужно найти любое базисное решение. В данном случае это легко сделать. Для этого достаточно взять в качестве базисных добавочные переменные х _3, х ₄, х ₅, х ₆. Так как коэффициенты при этих переменных образуют единичную матрицу, то отпадает необходимость вычислять определитель. Считая свободными переменные х ₁и х ₂равными нулю, получим базисное решение (0; 0; 120; 160; 120; 80), которое к тому же оказалось допустимым. Поэтому здесь отпадает надобность в применении первого этапа симплексного метода. Переходим сразу ко второму этапу, т. е. к поискам оптимального решения.

I ш а г. Базисные переменные: х _3, х ₄, х ₅, х ₆; свободные переменные: х ₁, х ₂. В системе (8) базисные переменные выразим через свободные. Для того чтобы судить, оставить ли свободные переменные в числе свободных или их выгоднее с точки зрения приближения к оптимальному решению перевести в базисные, следует выразить через них и линейную форму (в данном случае она уже выражена через переменные х ₁и х ₂).Тогда получим

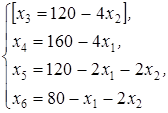(9)

F = 2 х ₁+ 3 х ₂.

При x ₁ = х ₂ = 0 имеем х ₃ = 120, х ₄= 160, x ₅= 120, х ₆ = 80, что дает базисное решение (0; 0; 120; 160; 120; 80), которое мы приняли за исходное. При этом базисном решении значение линейной формы F = 2 х ₁+ 3 х ₂= 0.

Когда мы полагали x ₁ = х ₂ = 0 (завод ничего не выпускает), была поставлена цель — найти первое, безразлично какое, базисное решение. Эта цель достигнута. Теперь от этого первоначального решения нужно перейти к другому, при котором значение линейной формы увеличится. Из рассмотрения линейной формы видно, что ее значение возрастает при увеличении значений переменных х ₁и х ₂. Иными словами, эти переменные невыгодно считать свободными, т. е. равными нулю, их нужно перевести в число базисных. Это и означает переход к новому базисному решению. При симплексном методе на каждом шаге решения предполагается перевод в число базисных только одной из свободных переменных. Переведем в число базисных переменную х ₂, так как она входит в выражение линейной формы с большим коэффициентом.

Как только одна из свободных переменных переходит в число базисных, одна из базисных должна быть переведена на ее место в число свободных. Какую же из четырех базисных переменных нужно вывести? Ответить на этот вопрос помогут следующие рассуждения.

Значение х ₂ необходимо сделать как можно большим, так как это соответствует конечной цели — максимизации F. Однако оказывается, что увеличение х₂ может продолжаться только до известных границ, а именно до тех пор, пока не нарушится требование неотрицательности переменных. Так, из первого уравнения системы (9) следует, что переменная х ₂не должна превышать числа 120/4, т. е. х ₂≤30, поскольку только при этих значениях х ₂переменная х ₃остается положительной (если х ₂= 30, то х ₃ = 0; если же х ₂ >30, то х ₃ < 0). Из третьего уравнения системы (9) следует, что х ₂ ≤ 120/2, т. е. х ₂≤60, из четвертого — что х ₂≤80/2, т. е. х ₂≤40 (во второе уравнение переменная х ₂не входит). Всем этим условиям удовлетворяет х ₂≤30.

Иными словами, для ответа на вопрос, какую переменную нужно перевести в число свободных, нужно принять х ₂= min {120/4; 120/2; 80/2} = min {30; 60; 40} = 30. Тогда х ₃ = 0 и х ₃переходит в число свободных переменных, a x ₄и х ₅останутся положительными.

II ш а г. Базисные переменные: х ₂, x ₄, х ₅, х ₆; свободные переменные: х ₁ , х ₃. Выразим базисные переменные и линейную форму через свободные. В системе (9) берем то уравнение, из которого получено минимальное значение отношения свободного члена к коэффициенту при х ₂. В данном случае это первое уравнение, которое выделено рамкой. Выразив из этого уравнения х ₂, имеем х ₂= 30 — 0,25 х ₃. Подставим это выражение х ₂во все остальные уравнения системы (9) и в линейную форму F и, приведя подобные члены, получим

(10)

F = 90+2 х ₁-0,75 х ₃.

При x ₁= х ₃= 0 имеем F = 90. Это уже лучше, чем на I шаге, но не искомый максимум. Дальнейшее увеличение функции F возможно за счет введения переменной х ₁в число базисных; так как эта переменная входит в выражение F с положительным коэффициентом, поэтому ее увеличение приводит к увеличению линейной формы и ее невыгодно считать свободной, т. е. равной нулю.

Для ответа на вопрос, какую переменную вывести из базисных в свободные, примем х ₁= min {160/4; 60/2; 20/1} = 20. Тогда х ₆ =0 и х₆ переходит в число свободных переменных, a x ₄и х ₅остаются при этом положительными.

Первое уравнение не используется при нахождении указанного минимума, так как х ₁не входит в это уравнение.

III шаг. Базисные переменные: х ₁, х ₂, x ₄, х ₅; свободные переменные: x ₃, х ₆. Выразим основные переменные и линейную форму через свободные. Из последнего уравнения системы (10) (выделено) имеем х ₁=20 + 0,5 х ₃ — х ₆. Подставляя это выражение в остальные уравнения и в линейную форму, получим:

(11)

F =130+0,25 х ₃ - 2 х ₆.

Из выражения линейной формы следует, что ее максимальное значение еще не получено, так как возможно увеличение F за счет введения в базисные переменной х ₃(она имеет положительный коэффициент). Полагаем х ₃= min {∞; 30/0,25; 80/2; 20/0,5} = 40.

Здесь мы впервые встречаемся с двумя положениями, которые требуют дополнительных разъяснений.

Во-первых, хотя переменная х ₃и входит в выражение для х ₁[первое уравнение системы (11)], но имеет положительный коэффициент и при любом возрастании х ₃переменная х ₁не может стать отрицательной. Иными словами, в первом уравнении никаких ограничений на возрастание переменной х ₃не накладывается, поэтому мы условно пишем ∞. Условимся в дальнейшем пользоваться этим же обозначением, если переменная, вновь вводимая в число базисных, не входит в какое-либо уравнение системы ограничений.

Во-вторых, мы получим два одинаковых минимальных значения, равные 40. Если х ₃ = 40, то х ₄= 0 и х ₅= 0, т. е. напрашивается вывод, что вместо одной переменной нужно перевести в число свободных сразу две: х ₄и х ₅. Но число базисных переменных не должно быть меньше четырех. Поэтому одну из переменных (x ₄или х ₅)оставляют в числе основных, но при этом ее значение считают равным нулю, т. е. полученное на следующем шаге базисное решение оказывается вырожденным. Оставим, например, x ₄в числе базисных переменных, а х ₅ переведем в число свободных.

IV шаг. Базисные переменные: x ₁, x ₂, x ₃, x ₄; свободные переменные: х ₅, х ₆. Выразим базисные переменные и линейную форму F через свободные, начав это выражение из четвертого уравнения системы (11). Получаем:

F = 140-0,5 х ₅ -х ₆.

Так как в выражение линейной формы переменные х ₅и х ₆входят с отрицательным коэффициентами, то никакое увеличение F за счет этих переменных невозможно.

Отсутствие на каком-то шаге симплексного метода в выражении линейной формы F, максимум которой ищется, неосновных переменных с положительными коэффициентами является критерием оптимальности.

Следовательно, на IV шаге критерий оптимальности достигнут и задача решена. Оптимальным служит решение (40;20;40;0;0;0), при котором F_mаx= 140. Таким образом, для получения наибольшей прибыли, равной 140 ден. ед., из данных запасов древесины завод должен изготовить 40 шкафов и 20 буфетов. При этом древесина II, III и IV видов окажется использованной полностью, а 40 ед. древесины I вида останутся неизрасходованными.

Задача 5. На свиноферме производится откорм свиней. Известно, что каждая свинья должна ежедневно получать не менее 6 ед. вещества К, 8 ед. вещества L и 12 ед. вещества М (вещества К, L, М могут, в частности, означать жиры, белки и углеводы). Для откорма свиней можно закупить три вида кормов: I, II и III (например, картофель, жмых и комбикорм). Содержание каждого вещества в различных видах корма и стоимость единицы каждого корма приведены в таблице 10. Требуется обеспечить наиболее дешевый рацион откорма.

Таблица 10

 

Вид корма	Вещества	Стоимость единицы корма
К	L	М
I
II
III		1,5		2,5

Решение. Составим экономико-математическую модель задачи. Пусть х ₁, х ₂и х ₃, — количество единиц соответственно I, II и III видов корма. Требуется найти минимум линейной формы F = 2 х ₁+3 х ₂+2,5 х ₃ при следующих ограничениях:

Введя добавочные неотрицательные переменные x ₁, х ₂и х ₃, сведем систему неравенств к системе уравнений

Проще всего получить базисное решение последней системы, если за базисные взять добавочные переменные х ₄, х ₅и x ₆. Правда, базисное решение (0, 0; 0; -6;-8;-12), в котором эти переменные являются базисными, — недопустимое. Поэтому сначалавоспользуемся симплексным методом для перехода к какому-либо допустимому базисному решению,

I шаг. Базисные переменные: x ₄, х ₅, х ₆; свободные переменные: х ₁, х ₂, х ₃. Выразим базисные переменные через свободные (на этом этапе линейная форма не рассматривается):

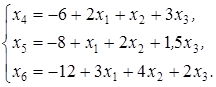
Переведем в базисные переменную х ₁. Для этого положим х ₁=min {3; 8; 4}=3. При х ₁= 3 имеем x ₄=0 и x ₄переходит в свободные переменные.

II шаг. Базисные переменные: х ₁, х ₅, х ₆; свободные переменные: х ₂, х ₃; х ₄. Выразив x ₁из первого уравнения системы и подставив полученное выражение в остальные уравнения, приходим к следующей системе:

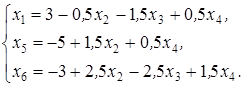
Базисное решение (3; 0; 0; 0;-5;-3) хотя и является недопустимым, но все-таки лучше, чем на I шаге, поскольку содержит уже только две отрицательные компоненты.

Переведем теперь в базисные переменную х ₄. Находим x ₄ = min{∞; 10; 2}= =2. При х ₄ =2 имеем х ₆ = 0 и х ₆переходит в свободные переменные.

III шаг. Базисные переменные: х ₁, x ₄, x ₅; свободные переменные: х ₂, x ₃, х ₆. Выразив из системы базисные переменные через свободные, получим

Переводим в базисные переменную x ₆. Полагаем х ₆=min{∞;∞;12}=12. При х ₆=12 имеем х ₅ = 0 и х ₅переходит в свободные переменные.

IV шаг. Базисные переменные: х ₁, x ₄, х ₆; свободные переменные х ₂, x ₃, х ₅. Выразив из системы базисные переменные через свободные, имеем

Полученное на этом шаге базисное решение (8; 0; 0; 10; 0; 12) является допустимым, и первый этап симплексного метода закончен.

Переходим ко второму этапу, т. е. будем искать оптимальное решение.

Проверим сначала, не является ли найденное допустимое базисное решение оптимальным. Для этого выразим линейную форму F = 2 х ₁+ 3 х ₂+ +2,5 х ₃ через свободные переменные. Подставив вместо х ₁ее выражение из первого уравнения системы и приведя подобные члены, получим F =16- х ₂- - 0,5 х ₃+ 2 х ₅.

В данной задаче речь идет о минимизации функции цели, поэтому выгодны те переменные, которые входят в выражение линейной формы с отрицательными коэффициентами. В данном случае таких переменных две: х ₂и х ₃.

Переведем в основные переменную х ₂. Положим х ₂ =min{4; 10/3; 6}= = 10/3. При х ₂ = 10/3 имеем х ₄ = 0 и х ₄ переходит в свободные переменные.

V шаг. Базисные переменные: х ₁, x ₂, х ₆ ; свободные переменные: х ₃, x ₄, х ₅. Выразим из системы базисные переменные и линейную форму через свободные:

Переводим в базисные переменную х ₃. Полагаем х ₃=min { }= . При х ₃ = 8/9 имеем х ₁= 0 и х ₁переходит в свободные переменные.

VI шаг. Базисные переменные х ₂, х ₃, х ₆; свободные переменные: х ₁, х ₄, х ₅.Выразим из системы базисные переменные и линейную форму через свободные:

В выражение F все переменные входят с положительными коэффициентами, а это означает, что критерий оптимальности при отыскании минимума линейной формы выполнен.

Таким образом, оптимальным служит решение (0; 10/3; 8/9; 0; 0; 28/9). При этом F _mln = 110/9 ≈12,22 ден. ед.

Итак, чтобы обеспечить наиболее дешевый рацион питания, нужно в основном покупать самый дорогой корм II вида, корма III вида нужно закупать почти в четыре раза меньше, а корм I вида хотя и самый дешевый, но невыгодный. При этом оптимальном решении будут обеспечены нормы вещества К и L, а вещества М окажется на 28/9 ≈3,11 ед. больше нормы.

Симплексные таблицы

Рассмотренный симплексный метод решения ЗЛП в предыдущем пункте можно свести к записи однотипно заполняемых таблиц. Осуществить это возможно, придерживаясь следующего алгоритма:

1. Привести задачу линейного программирования к каноническому виду.

2. Найти начальное опорное решение с базисом из единичных векторов и коэффициенты разложений векторов условий по базису опорного решения. Если опорное решение отсутствует, то задача не имеет решения в силу несовместности системы ограничений.

3. Вычислить оценки разложений векторов условий по базису опорного решения и заполнить симплексную таблицу.

4. Если выполняется признак единственности оптимального решения (для любого вектора условий, не входящего в базис, оценка отлична от нуля), то решение задачи заканчивается.

5. Если выполняется условие существования множества оптимальных решений (оценка хотя бы одного вектора условий, не входящего в базис, равна нулю), то путем простого перебора находят все оптимальные решения.

6. Если выполняются условия отсутствия оптимального решения вследствие неограниченности целевой функции (не имеет решения, если для какого-либо из векторов условий с оценкой, противоречащей признаку оптимальности, среди коэффициентов разложения по базису опорного решения нет положительного), то задача не имеет решения ввиду неограниченности целевой функции.

7. Если пункты 4-6 алгоритма не выполняются, находят новое опорное решение с использованием условий нахождения оптимального решения.

Пример 4. Решить задачу табличным симплексным методом.

F(Х) = 9 х ₁ + 5 х ₂+4 х ₃ + 3 х ₄ + 2 х ₅ →max.

Решение. Приводим задачу к каноническому виду. Для этого в левую часть первого ограничения-неравенства типа «≤» вводим дополнительную переменную х ₆ с коэффициентом +1. В целевую функцию переменная х ₆ входит с коэффициентом 0 (т.е. не входит). Получаем

F(Х) = 9 х ₁ + 5 х ₂+4 х ₃ + 3 х ₄ + 2 х ₅ +0 х ₆→max.

Находим начальное опорное решение. Для этого свободные (неразрешенные) переменные приравниваем к нулю х ₁= х ₂= х ₃=0. Получаем опорное решение Х ₁=(0, 0, 0, 24, 30, 6) с единичным базисом Б ₁=(А ₄, А ₅, А ₆).

Вычисляем оценки разложений векторов условий по базису опорного решения, используя формулу (Δ _к = С_бХ_к-с_к, где С_б =(с ₁ ,с ₂ ,…,с_т)― вектор коэффициентов целевой функции при базисных переменных; Х_к =(х _{1 к} ,х _{2 к} ,…,х_тк)-вектор коэффициентов разложения вектора по базису опорного решения; с_к ― коэффициент целевой функции при х_к):

Δ₁= С _б Х ₁ - с ₁= (0, 3, 2) · (1, 1, 2) - 9 = 0 + 3 + 4 - 9 = -2;

Δ₂ = С_бХ ₂ -с ₂ = (0, 3, 2) · (-2, 2, 1) - 5 = 0 + 6 + 2 - 5 = 3;

Δ₃ = С_бХ ₃- с ₃= (0, 3, 2) · (2, 1, -4) - 4 = 0 + 3 - 8 - 4 = -9;

Δ ₄ = С_бХ ₄- с ₄ = (0, 3, 2) · (0, 1, 0) - 3 = 0 + 3 + 0 - 3 = 0;

Δ ₅ = С_бХ₅ - с ₅ = (0, 3, 2) · (0, 0, 1) - 2 = 0 + 0 + 2 - 2 = 0;

Δ ₆ = С_бХ₆ - с ₆ = (0, 3, 2) ·(1, 0, 0) - 0 = 0 + 0 + 0 - 0 = 0.

Оценки векторов, входящих в базис, всегда равны нулю. Обычно эти вычисления проводятся устно. Опорное решение, коэффициенты разложений и оценки разложений векторов условий по базису опорного решения записываются в симплексную таблицу. Сверху над таблицей для удобства вычислений оценок записываются коэффициенты целевой функции. В первом столбце «Б»записываются векторы, входящие в базис опорного решения. Порядок записи этих векторов в симплексной таблице соответствует номерам разрешенных неизвестных в уравнениях-ограничениях. Во втором столбце таблицы «С _б» записываются коэффициенты целевой функции при базисных переменных в том же порядке. При правильном расположении коэффициентов целевой функции в столбце «С _б» оценки единичных векторов, входящих в базис, всегда равны нулю.

В последней строке таблицы с оценками Δ _к в столбце «А ₀»записывается значение целевой функции на опорном решении F (X ₁).

9 5 ↓4 3 2 0

Б	С б	А 0	А 1	А 2	А 3	А 4	А 5	А 6	θ1	θ3
←А 6				-2
А 4
А 5					-4					-
Δ к		-2		-9

Начальное опорное решение не является оптимальным, так как оценки Δ₁=-2, Δ₃ = -9 для векторов А ₁и А ₃противоречат признаку оптимальности. Для оптимальности опорного решения в задаче на максимум требуется неотрицательность оценок для всех векторов условий.

По теореме об улучшении опорного решения, если в задаче на максимум хотя бы один вектор имеет отрицательную оценку, то можно найти новое опорное решение, на котором значение целевой функции будет больше.

Определим, введение какого из двух векторов приведет к большему приращению целевой функции. Приращения целевой функции найдем по формуле Δ F_k =-θ_{0 к} ×Δ _к. Вычислим значения параметра -θ_{0 к} для первого и третьего столбцов по формуле θ_{0 к} = , при х_ik >0, где к ― номер вектора, вводимого в базис; l - номер вектора, выводимого из базиса; х_i0 ― координаты опорного решения; х_ik - коэффициент разложения вектора А_к по базису опорного решения. Получаем θ₀₁ = 6 при l= 1 (где l — номер строки) и θ₀₃ = 3 при l = 1. Находим приращение целевой функции при введении в базис первого вектора Δ F ₁= -6·(-2) = 12 и третьего вектора Δ F ₃= -3·(-9) = 27. Следовательно, для наиболее быстрого нахождения оптимального решения необходимо ввести в базис опорного решения вектор А ₃вместо первого вектора базиса А ₆, так как минимум параметра θ₀₃ достигается в первой строке (l = 1).

Далее выполним преобразование с элементом х ₁₃= 2, получим второе опорное решение Х ₂=(0,0,3,21,42,0) с базисом Б ₂= (A ₃ , A ₄, А ₅)(следующая таблица). Это решение не является оптимальным, так как вектор А ₂имеет отрицательную оценку Δ₂ = -6. Для улучшения решения необходимо ввести вектор А ₂в базис опорного решения.

 

Б	С б	А 0	А 1	А 2	А 3	А 4	А 5	А 6	θ2
А 3			½	-1				½	-
←А 4			½					-½
А 5				-3					-
Δ к		5/2	-6				9/2

Определим номер вектора, выводимого из базиса. Для этого вычислим параметр θ₀₂ для второго столбца, он равен 7 при l =2. Следовательно, из базиса выводим второй вектор базиса А ₄. Выполним преобразование с элементом х ₂₂= 3, получим третье опорное решение Х ₃ = (0, 7, 10, 0, 63, 0) с базисом Б ₂ = (А ₃, А ₂, А ₅). Это единственное оптимальное решение, так как для всех векторов, не входящих в базис, оценки разложений по базису опорного решения положительны: Δ₁=7/2, Δ₄=2, Δ₆=7/2.

Б	С б	А 0	А 1	А 2	А 3	А 4	А 5	А 6
А 3			2/3			1/3		1/3
←А 2			1/6			1/3		-1/6
А 5			9/2					3/2
Δ к		7/2					7/2

Ответ: max F(X) = 201 при X ^*= (0, 7,10, 0, 63).

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: