Задача с двумя переменными

 

Пусть требуется найти максимальное значение функции

F(X) = с₁ х₁ + с ₂ х ₂(6)

при ограничениях

(7)

Допустим, что система ограничений (7) совместна, т.е. имеет решение, а многоугольник ее решений (ОДР) ограничен. Каждое из неравенств (7) определяет полуплоскость с границей , i = 1, 2,..., т или х ₁ = 0, х ₂ = 0. Представим этот многоугольник на плоскости Ох₁х ₂ (рисунок 1).

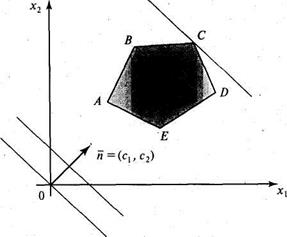
Рисунок 1 – Область допустимых решений.

 

Линейная функция (6) при фиксированных значениях F(X) является уравнением прямой линии c ₁ x ₁+ c ₂ x ₂=const.

Изобразим прямую, соответствующую линейной функции, при F(X) = 0. Эта прямая пройдет через начало координат. Другим значениям F(X) будут соответствовать прямые, параллельные друг другу.

Прямая, уравнение которой получено из целевой функции задачи при равенстве ее постоянной величине, называется линией уровня.

Известно, что коэффициенты при переменных в линейном уравнении являются координатами нормального вектора к соответствующей прямой или плоскости. Следовательно, нормальный вектор линий уровня и имеет координаты с ₁ и с ₂, т.е. = (с₁, с ₂).

Если перемещать линию уровня параллельно ее начальному положению в направлении вектора , то для данного случая (рисунок 2) последней точкой, в которой линия уровня коснется ОДР, окажется точка С. Линия уровня, имеющая общие точки с ОДР и расположенная так, что ОДР целиком находится в одной из полуплоскостей, называется опорной прямой.

Теорема 2. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали, и убывают при перемещении в противоположном направлении.

Доказательство. Пусть F(X) = c ₁ x ₁+ c ₂ x ₂ — целевая функция. Изобразим систему координат О х ₁ х ₂ и нормаль = (с ₁, с ₂), проведенную из начала координат (рисунок 2). Проведем две линии уровня перпендикулярно вектору . Возьмем на первой линии точку Р(х'₁, х'₂), а на второй линии точку М(х₁, х₂) так, чтобы вектор РМ был параллелен вектору . Проведем векторы ОМ и ОР. Вектор ОМ имеет координаты х₁, х₂, т.е. координаты точки М, а вектор ОР ― координаты точки Р.

Значение целевой функции в точке М

F(M)= c ₁ x ₁+ c ₂ x ₂= · ОМ= (ОР + РМ)= · ОР+ · РМ.

Рисунок 2

Но · ОР равно значению целевой функции в точке Р, т.е. F(P). По определению скалярного произведения · РМ = где φ — угол между векторами и РМ. Если и РМ направлены в одну сторону, то φ = 0 и cos φ = 1. Тогда F(M)= F(P)+ F(M)> F(P). Если и РМ направлены в противоположные стороны, то cos φ = -1 и F(M) < F(P). Что и требовалось доказать.

Алгоритм решения ЗЛП с двумя переменными графическим методом таков:

1. Строится область допустимых решений.

2. Строится вектор = (с ₁, с ₂) с точкой приложения в начале координат.

3. Перпендикулярно вектору проводится одна из линий уровня, например линия уровня, соответствующая уравнению с ₁ х ₁ + с₂х₂ = 0.

4. Линия уровня перемещается до положения опорной прямой. На этой прямой и будет находиться максимум или минимум функции.

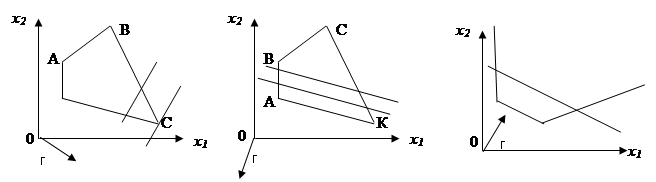В зависимости от вида ОДР и целевой функции F(X) задача может иметь единственное решение (рисунок 3, а), бесконечное множество решений (рисунок 3, б)или не иметь ни одного оптимального решения (рисунок 3, в).

 

a) б) в)

Рисунок 3

Пример 1. Решить задачу линейного программирования графическим методом: F(X)= 2 x ₁+4 x₂ → max,

Решение.

Рисунок 4 - Область допустимых решений задачи.

 

Изобразим на плоскости систему координат О х ₁ х ₂ и построим граничные прямые области допустимых решений (номера прямых соответствуют их порядковому номеру в системе). Область допустимых решений определяется многоугольником OABCD (рисунок 4).

Для линий уровня 2 х ₁ + 4 х ₂ = с (с = const) строим нормальный вектор = (2,4). Перпендикулярно вектору построим одну из линий уровня (на рисунке 4 она проходит через начало координат). Так как задача на максимум, то перемещаем линию уровня в направлении вектора до опорной прямой. В данном случае опорной прямой является прямая, проходящая через точку пересечения граничных прямых L ₁ и L ₂, т.е. через точку В = L ₁∩ L₂. Для определения координат точки В решаем систему уравнений .

Получаем х ₁ = 3, х₂ = 6. Это и будет оптимальное решение данной задачи, которому соответствует максимальное значение целевой функции

max F(X) = 2 · 3 + 4 · 6 = 30.

Пример 2. Найти минимум функции F(X)= 2 x ₁+ x₂ → min при ограничениях

Рисунок 5

Отличие этого примера от предыдущего состоит в том, что здесь ищется не максимум, а минимум функции F. Областью решений данной системы ограничений является треугольник АВС (рисунок 5). На рисунке изображены также исходная линия уровня и вектор q = (2; 1), показывающий направление движения этой линии для достижения максимума функции F. Так как требуется найти минимум этой функции, то будем передвигать исходную линию уровня в сторону, противоположную вектору q. Как видно из рисунке 5, минимум функции F достигается в угловой точке А, координаты которой служат решением системы уравнений

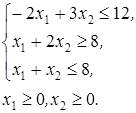
Отсюда А (6/7; 25/7) и F _min = 37/7.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: