Общие методы решения конечных игр. Сведение их к задачам линейного программирования

Мы рассматривали до сих пор только самые элементарные игры типа 2х п, которые могут быть весьма просто решены и допускают удобную и наглядную геометрическую интерпретацию.

В общем случае решение игры m x n представляет довольно трудную задачу, причём сложность задачи и объём вычислений резко возрастает с увеличением т и п.

При решении игр т х п на практике удобнее пользоваться не геометрическими аналогиями, а расчётными аналитическими методами, тем более, что для решения задачи на вычислительных машинах эти методы единственно пригодны.

Решение любой конечной игры m x n может быть приведено к задаче линейного программирования.

Пусть дана игра m x n с m стратегиями А₁, А₂,..., А _т игрока А и п стратегиями В₁, В₂,..., В _п игрока В и задана платежная матрица ║ а_ij ║. Требуется найти решение игры, т.е. две оптимальные смешанные стратегии игроков А и В:

(17)

где р ₁+ р ₂+… + р_m =1, q ₁+ q ₂+…+ q_n =1.

Оптимальная стратегия должна обеспечивать нам выигрыш, не меньшей v, при любом поведении противника, и выигрыш, равный v, при его оптимальном поведении (стратегия ). Цена игры v не известна. Будем считать, что v >0, для чего нужно, чтобы все элементы матрицы ║ а_ij ║ были неотрицательными. Этого можно добиться, прибавляя к элементам ║ а_ij ║ достаточно большую положительную величину L, при этом цена игры увеличивается на L, а решение не изменится [16].

Пусть мы выбрали свою оптимальную стратегию . Тогда наш средний выигрыш при стратегии B _j противника будет равен:

а_j = p₁a _{1 j} + p ₂ a _{2 j} + …+ p_ma_mj. (18)

Оптимальная стратегия обладает тем свойством, что при любом поведении противника обеспечивает выигрыш не меньший, чем v_j, следовательно, любое из чисел a_j не может быть меньше v. Получаем ряд условий:

(19)

Разделим неравенства на положительную величину v и обозначим

. (20)

Тогда условия системы запишутся в виде

, (21)

где - необязательные числа.

Т.к. p ₁+ p ₂ +... + p_m =1, то величины удовлетворяют условию .

Мы хотим сделать свой гарантированный выигрыш максимально возможным; очевидно, при этом правая часть последнего равенства принимает минимальное значение.

Таким образом, задача нахождения решения игры сводится к следующей задаче линейного программирования: определить неотрицательные величины удовлетворяющие последней системе, так, чтобы их сумма была минимальной.

Задача второго игрока является двойственной по отношению к задаче первого игрока. Можно найти решение одного из игроков, а затем по теоремам двойственности - решение другого.

Пример 22. Требуется найти решение игры 3х3 с матрицей:

Таблица 19 - Игра 3х3.

 

В А	В1	В2	В3
А1		-3
А2	-3		-5
А3		-5

Решение. Чтобы сделать все а_ij ≥0, прибавим ко всем элементам матрицы L=5. Получим матрицу (табл. 10).

При этом цена игры увеличится на 5, а решение не изменится.

, где .

Таблица 20 - Преобразованная матрица.

 

В А	В1	В2	В3
А1
А2
А3

 

Чтобы избавится от знаков неравенства, введем фиктивные переменные z₁, z₂, z₃, тогда имеем

.

Линейная форма Ф имеет вид: .

Выразим Ф через z₁, z₂, z₃ решая систему получим:

.

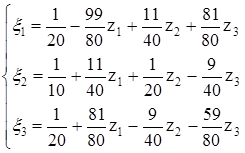Тогда .

В выражении коэффициенты при всех z положительны, значит любое увеличение z₁, z₂, z₃ сверх нуля может привести к увеличению формы Ф, а нам нужно чтобы она была минимальной. Следовательно, z₁=z₂=z₃=0. Тогда , v =5.

Находим , или умножая их на v:

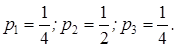
Таким образом, оптимальная стратегия А найдена:

.

Зная цену игры, можно уже известными способами найти оптимальную стратегию соперника:

.

Для этого воспользуемся любыми двумя полезными стратегиями, например А ₂ и А ₃ и напишем уравнения:

,

откуда q ₁= q ₃=1/4; q ₂=1/2. Оптимальная стратегия противника будет такой же, как наша:

.

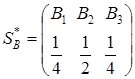Теперь вернёмся к первоначальной (не преобразованной) игре. Для этого нужно только от цены игры v =5 отнять величину L=5, прибавленную к элементам матрицы. Получается цена исходной игры v =0. Следовательно, оптимальные стратегии обеих сторон обеспечивают выигрыш, равный нулю; игра в одинаковой мере выгодна или невыгодна для обеих сторон.

В рассмотренной выше задаче игра задавалась платежной матрицей, которую сводили к модели линейного программирования. И, наоборот, задача линейного программирования может быть сведена к матричной игре.

Если задача линейного программирования имеет вид F (x)= , при ограничениях: x_j ≥ 0, i=1,…, m, j=1,…, n, то матричная игра определяется платежной матрицей размера (т + п + 1) вида , где А — матрица коэффициентов при неизвестных системы ограничений задачи линейного программирования; В — матрица свободных членов; С — матрица коэффициентов при неизвестных целевой функции; А^t, В^t, С^t — транспонированные матрицы А, В, С.

Если задача линейного программирования имеет вид F (x)= , при ограничениях: x_j ≥ 0, i=1,…, m, j=1,…, n, то матричная игра определяется платежной матрицей размера (т + п + 1) вида

.

Пример 23. Построить матричную игру, заданную задачей линейного программирования F(x) = 2х ₁ + 3 x ₂ → max при ограничениях:

x ₁, x ₂ ≥0.

Решение. Обозначим: , , .

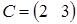Транспонированные матрицы:

, , , т + п + 1=2+2+1=5.

Ответ: Игру, определяемую данной задачей линейного программирования, можно записать матрицей:

 

Игры с «природой».

В рассмотренных выше матричных играх предполагалось, что в них принимают участие два игрока, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша (уменьшение проигрыша). Однако в некоторых задачах, приводящихся к игровым, имеется неопределенность, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос и т.д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности. Такие игры называются играми с природой. Человек в играх с природой старается действовать осмотрительно, второй игрок (природа, покупательский спрос) действует случайно.

Условия игры задаются матрицей (а_ij) _{т х п} .

Имеется ряд критериев, которые используются при выборе оптимальной стратегии [11]. Рассмотрим некоторые из них.

1. Критерий Вальде. Рекомендуется применять максиминную стратегию. Она достигается из условия max mina_ij и совпадает с нижней ценой игры. Критерий является пессимистическим, считается, что природа будет действовать наихудшим для человека образом.

2. Критерий максимума. Он выбирается из условия max maxa_ij. Критерий является оптимистическим, считается, что природа будет наиболее благоприятна для человека.

3. Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле max {α mina_ij + (1 — α) max a_ij }, где α — степень оптимизма — изменяется в диапазоне [0,1].

Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего для человека поведения природы. При α = 1 критерий превращается в критерий Вальде, при α = 0 — в критерий максимума. На α оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем хуже последствия ошибочных решений, больше желания застраховаться, тем α ближе к единице.

4. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии.

Элемент матрицы рисков (r_ij) находится по формуле

r_ij = max a_ij — а _ij, (22)

где max a_ij — максимальный элемент в столбце исходной матрицы.

Оптимальная стратегия находится из выражения

min { max(max a_ij — а_ij) }. (23)

Пример 24. Фирма "Фармацевт" — производитель медикаментов и биомедицинских изделий в регионе. Известно, что пик спроса на некоторые лекарственные препараты приходится на летний период (препараты сердечно-сосудистой группы, анальгетики), на другие — на осенний и весенний периоды (антиинфекционные, противокашлевые).

Затраты на 1 усл. ед. продукции за сентябрь-октябрь составили: по первой группе (препараты сердечно-сосудистые и анальгетики) — 20 р.; по второй группе (антиинфекционные, противокашлевые препараты) — 15 р.

По данным наблюдений за несколько последних лет службой маркетинга фирмы установлено, что она может реализовать в течение рассматриваемых двух месяцев в условиях теплой погоды 3050 усл. ед. продукции первой группы и 1100 усл. ед. продукции второй группы; в условиях холодной погоды — 1525 усл. ед. продукции первой группы и 3690 усл. ед. второй группы.

В связи с возможными изменениями погоды ставится задача — определить стратегию фирмы в выпуске продукции, обеспечивающую максимальный доход от реализации при цене продажи 40 р. за 1 усл. ед. продукции первой группы и 30 р. — второй группы.

Решение. Фирма располагает двумя стратегиями:

А ₁— в этом году будет теплая погода; А ₂— погода будет холодная.

Если фирма примет стратегию А ₁и в действительности будет теплая погода (стратегия природы B ₁ ), то выпущенная продукция (3050 усл. ед. препаратов первой группы и 1100 усл. ед. второй группы) будет полностью реализована и доход составит

3050 · (40 - 20) + 1100 · (30 - 15) = 77500 р.

В условиях прохладной погоды (стратегия природы В ₂)препараты второй группы будут проданы полностью, а первой группы только в количестве 1525 усл. ед. и часть препаратов останется нереализованной. Доход составит

1525 • (40 - 20) + 1100 • (30 - 15) - 20 • (3050 - 1525) = 16 500 р.

Аналогично, если фирма примет стратегию А ₂и в действительности будет холодная погода, то доход составит

1525 • (40 - 20) + 3690 • (30 - 15) = 85850 р.

При теплой погоде доход составит

1525 • (40 - 20) + 1100 • (30 - 15) - (3690 - 1100) • 15 = 8150 р.

Рассматривая фирму и погоду в качестве двух игроков, по­лучим платежную матрицу

В ₁ В ₂

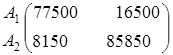
α = тах (16 500, 8150) = 16 500 р., β = min (77500, 85 850) = 77500 р.

Цена игры лежит в диапазоне 16 500 р. ≤ v ≤77 500 р.

Из платежной матрицы видно, что при всех условиях доход фирмы будет не меньше 16 500 р., но если погодные условия совпадут с выбранной стратегией, то доход фирмы может составить 77 500 р.

Найдем решение игры.

Обозначим вероятность применения фирмой стратегии А ₁через х ₁, стратегии А ₂— через х ₂, причем х ₁=1 — х ₂. Решая игру графическим методом, получим х ₁= 0,56; х ₂ = 0,44, при этом цена игры v = 46 986 р.

Оптимальный план производства лекарственных препаратов составит

0,56 · (3050; 1100) + 0,44 · (1525; 3690) = (2379; 2239,6).

Таким образом, фирме целесообразно производить в течение сентября и октября 2379 усл. ед. препаратов первой группы и 2239,6 усл. ед. препаратов второй группы, тогда при любой погоде она получит доход не менее 46 986 р.

В условиях неопределенности, если не представляется возможным фирме использовать смешанную стратегию (договоры с другими организациями), для определения оптимальной стратегии фирмы используем критерии природы.

1. Критерий Вальде:

max (mina_ij) = тах (16500,8150) = 16 500 р.,

фирме целесообразно использовать стратегию А ₁.

2. Критерий максимума:

max(maxa_ij) = max (77500,85850) = 85850 р.,

целесообразно использовать стратегию А ₂.

3. Критерий Гурвица: для определенности примем α = 0,4,

тогда для стратегии фирмы А ₁

α min а_ij + (1 — α) max а_ij = 0,4 • 16 500 + (1 - 0,4) • 77 500 = 53100 р.;

для стратегии А ₂

α min а_ij + (1 — α) max а_ij = 0,4 • 8150 + (1 - 0,4) • 85 850 = 54 770 р.,

max (53100,54 770) = 54 770 р.,

фирме целесообразно использовать стратегию А ₂.

4. Критерий Сэвиджа. Максимальный элемент в первом столбце — 77 500, во втором столбце — 85 850.

Элементы матрицы рисков находятся из выражения

r_ij = max a_ij — а _ij, (16)

откуда r ₁₁= 77500 - 77500 = 0, r ₁₂ = 85850 - 16 500 = 69350,

r ₂₁ = 77500 - 8150 = 69350, r ₂₂ = 85 850 - 85 850 = 0.

Матрица рисков имеет вид

,

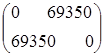min { max (maxа_ij - а_ij)} = min (69 350, 69 350) = 69350 р.,

целесообразно использовать стратегию А ₁или А ₂.

Следовательно, фирме целесообразно применять стратегию А ₁или А ₂.

Отметим, что каждый из рассмотренных критериев не может быть признан вполне удовлетворительным для окончательного выбора решений, однако их совместный анализ позволяет более наглядно представить последствия принятия тех или иных управленческих решений.

При известном распределении вероятностей различных состояний природы критерием принятия решения является максимум математического ожидания выигрыша.

Пусть известно для рассматриваемой задачи, что вероятности теплой и холодной погоды равны и составляют 0,5, тогда оптимальная стратегия фирмы определяется так:

max {(0,5·77500+0,5·16 500);(0,5·8150 + 0,5·85850)}=(47000;47000)=47000 р.

Фирме целесообразно использовать стратегию А ₁или А ₂.

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: