Основная теорема теории игр

Каждая конечная игра имеет, по крайней мере, одно решение (возможно, в области смешанных стратегий) [4].

Выигрыш, получаемый в результате решения, называется ценой игры.

Следствие 2. Каждая конечная игра имеет цену.

Очевидно, что цена игры v всегда лежит между нижней ценой игры α и верхней ценой игры β: α< v <β.

Введём специальное обозначение для смешанных стратегий. Если, например, наша смешанная стратегия состоит в применении стратегий А₁, А₂, А₃ с частотами р₁, р₂, р₃, причём р₁+р₂+р₃=1, будем обозначать эту стратегию

.

Аналогично смешанную стратегию противника будем обозначать:

,

где q ₁, q ₂, q ₃ - частоты, в которых смешиваются стратегии В₁, В₂, В₃; q ₁+ q ₂+ q ₃=1.

Оптимальные стратегии, образующие решения игры, будем обозначать S_A*, S_B*.

Определение 11. Стратегии, входящие в решение игры, называются активными.

Определение 12. Игра, в которой все стратегии обеих сторон являются активными, называется полностью усреднённой.

Решение игры обладает замечательным свойством.

Теорема 14. Если один из игроков придерживается своей оптимальной смешанной стратегией, то выигрыш остаётся неизменным и равным цене игры v независимо от того, что делает другой игрок, если только он не выходит за пределы своих активных стратегий [15].

 

Элементарные методы решения игр. Игры 2x2 и 2х п.

 

Если игра m x n не имеет седловой точки, то нахождение решения есть вообще довольно трудная задача, особенно при больших т и п.

Эту задачу можно упростить, если уменьшить число стратегий, вычёркивая излишние стратегии: дублирующие и заведомо невыгодные.

Рассмотрим, например, игру с матрицей

Таблица 15 - Игра, представленная в виде матрицы.

В А	В1	В2	В3	В4
А1
А2
А3
А4

 

Стратегия А₃ в точности повторяет ("дублирует") стратегию А₁ поэтому любую из этих двух стратегий можно вычеркнуть.

Сравнивая почленно строки А₁ и A₂, видим, что каждый элемент строки А₂ меньше (или равен) соответствующего элемента строки А₁. Очевидно, мы никогда не должны пользоваться стратегией А₂; она заведомо является невыгодной. Вычёркивая А₃ и А₂, приводим матрицу к более простому виду.

Далее замечаем, что для противника стратегия В₃ заведомо невыгодна; вычёркивая её, приводим матрицу к окончательному виду.

Таблица 16 - Окончательная матрица игры.

 

 

В А	В1	В2	В4
А1
А4

 

Таким образом, игра 4x4 вычёркиванием дублирующих и заведомо невыгодных стратегий сведена к игре 2x3.

Замечание 2. Процедура вычёркивания дублирующих и заведомо невыгодных стратегий всегда должна предшествовать решению игры.

Наиболее простыми типами конечных игр, которые всегда можно решить элементарными способами, являются игры 2x2 и 2х п.

Рассмотрим игру 2x2 с матрицей (таблица 17).

Таблица 17 - Игра 2х2.

 

В А	В1	В2
А1	а 11	а 12
А2	а 21	а 22

 

Здесь могут встретиться два случая:

1. игра имеет седловую точку;

2. игра не имеет седловую точку. Решение

Первый случай. Если игра 2x2 имеет седловую точку, то решение очевидно: это - пара чистых стратегий, пересекающихся в седловой точке.

Замечание 3. В игре 2x2 наличие седловой точки всегда соответствует существованию заведомо невыгодых стратегий, которые должны быть вычеркнуты при предварительном анализе.

Второй случай. Если седловой точки нет, то α≠β. Требуется найти оптимальную смешанную стратегию игрока А:

.

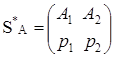Она отличается тем свойством, что, каковы бы ни были действия противника (если только он не выходит за пределы своих «полезных стратегий»), выигрыш будет равен цене игры v.

В игре 2x2 обе стратегии противника являются «полезными», - иначе игра имела бы решение в области чистых стратегий (седловую точку).

Значит, если мы придерживаемся своей оптимальной стратегии

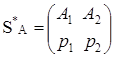, то противник может пользоваться любой из своих чистых стратегий В₁, В₂, не изменяя среднего выигрыша v.

Отсюда имеем два уравнения:

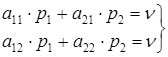. (15)

Из которых, принимая во внимание, что p₁ + р₂ = 1, получим:

. (16)

Цену игры v найдём, подставляя значение р₁, р₂ в любое уравнение (15). Если цена игры известна, то для определения оптимальной стратегии противника

достаточно одного уравнения, например: , откуда, учитывая, что q ₁+ q ₂ = 1, имеем

, q ₂ = 1- q _1. (17)

Пример 21. У нас (А) имеется два вида вооружения А₁ и А₂: у противника (В) -два вида помех: B₁ и В₂. Вероятность выполнения боевой задачи при различных комбинациях "вооружения" — "помехи" задана матрицей 2x2. Найти решение.

Таблица 18 - Заданная матрица игры.

 

В А	В1	В2	Минимумы строк
А1	0,2	0,8	0,2
А2	0,7	0,3	0,3*
Максимумы столбцов	0,7*	0,8

Решение.

1. α = 0,3; β = 0,7. Игра не имеет седловой точки.

2. По формуле (16) находим:

=

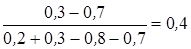
р₂ = 1 - p₁=1-0,4=0,6

3. Цена игры

v = a ₁₁·р₁+ a ₂₁·р₂=0,2·0,4+0,7·0,6=0,5

4. По формуле (17) находим

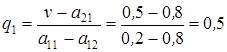; q ₂ = 1- q ₁=1-0,5=0,5

5. Оптимальные стратегии А и В будут:

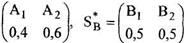S*_A=

Вывод. А должен в 40% всех случаях применять вооружение А₁, а в 60% -вооружения А₂. В должен в половине всех случаев применять помехи В₁, а в половине - помехи В₂. Если обе стороны, или, по крайней мере, одна из них, будут применять свои оптимальные стратегии, то вероятность выполнения боевой задачи будет равна v = 0,5.

 

Геометрическая интерпретация игры 2x2, игры 2x п.

Пусть имеется игра 2x2 (таблица 17).

Возьмём участок оси абсцисс длиной 1 и проведём через его концы А₁ и А₂ два перпендикуляра к оси абсцисс: ось I и II. На оси I будем откладывать выигрыш при стратегии А₁ на оси II - выигрыш при стратегии А₂. Рассмотрим стратегию противника В₁ она даёт две точки на осях I и II с ординатами, соответственно, а ₁₁ и а ₂₁. Проведём через эти точки прямую B₁B₁.

Рисунок 11

Очевидно, если мы при стратегии противника В₁ будем применять смешанную стратегию, то наш средний выигрыш, равный в этом случае a ₁₁p₁+ a ₂₁p₂, изобразится точкой М на прямой В₁В₁; абсцисса этой точки равна р₂. Прямую В₁В₁ изображающую выигрыш при стратегии В₁ будем условно называть "стратегией В₁". Очевидно, точно таким же образом может быть построена и стратегия В₂.

Рисунок 12

Нам нужно найти оптимальную стратегию S ^*_A, т.е. такую, для которой минимальный выигрыш (при любом поведении В) обращался бы в максимум. Для этого построим нижнюю границу выигрыша при стратегиях В₁В₂, т.е. ломаную B₁NB₂. Эта нижняя граница будет выражать минимальный выигрыш игрока А при любых его смешанных стратегиях; точка N, в которой этот минимальный выигрыш достигает максимума, и определяет решение и цену игры. Ордината точки N есть цена игры v, a её абсцисса равна р₂ - частоте применения стратегии А₂ в оптимальной смешанной стратегии S_A [6].

В нашем случае решение игры определялось точкой пересечения стратегий. Однако, это не всегда будет так. На рисунке 13 показан случай, когда, несмотря на наличие пересечения стратегий, решение даёт для обоих игроков чистые стратегии А₂ и В₂, а цена игры v = a ₂₂.

Рисунок 13

В данном случае матрица имеет седловую точку, и стратегия А₁ является заведомо невыгодной, т.к. при любой чистой стратегии противника она даёт меньший выигрыш, чем А₂.

В случае, когда заведомо невыгодная стратегия имеется у противника, геометрическая интерпретация имеет вид, представленный на рисунке 14.

Рисунок 14

В данном случае нижняя граница выигрыша совпадает со стратегией В₁ стратегия В₂ для противника является заведомо невыгодной.

Мы пришли к следующему графическому способу нахождения оптимальной стратегии:

1. построить линии стратегий В;

2. обвести нижнюю границу выигрыша;

3. найти на ней максимум, он будет равен цене игры v и разделит отре­зок между точками А₁ и А₂ в отношении р₂:р₁.

Оптимальную стратегию В можно найти, построив вместо нижней границы выигрыша верхнюю границу и на ней искать не максимум, а минимум.

Игра 2хп.

Совершенно аналогично может быть решена любая игра 2х п, где у нас имеются всего две стратегии, а у противника - произвольное число. Пусть мы располагаем двумя стратегиями: А₁ и А₂, а противник - " п " стратегиями: В₁, В₂,…, В_n. Матрица ║ a_{i j}║ задана; она состоит из двух строк и " п " столбцов. Аналогично случаю двух стратегий дадим задаче геометрическую интерпретацию; " п " стратегий изобразятся " п " прямыми. Строим нижнюю границу выигрыша (ломаную B₁MNB₂) и находим на ней точку N с максимальной ординатой. Эта точка даёт решение игры (стратегию ); ордината точки N равна цене игры v, а абсцисса равна частоте р₂ стратегии А₂.

Рисунок 15

В данном случае оптимальная стратегия противника получается применением смеси двух "полезных" стратегий: В₂ и В₄, пересекающихся в точке N. Стратегия В₃ является заведомо невыгодной, а стратегия В₁ - невыгодной при оптимальной стратегии S ^*_A.

Если А будет придерживаться своей оптимальной стратегии, то выигрыш не изменится, какой бы из своих "полезных" стратегий ни пользовался В, однако, он изменится, если В перейдёт к стратегиям B₁ или В₃.

В теории игр доказывается, что и любой конечной игры m x n имеется решение, в котором число "полезных" стратегий той и другой стороны не превосходит наименьшего из двух чисел m и n. В частности, из этого следует, что игры 2х п всегда имеют решение, в котором с той и другой стороны участвует не более двух "полезных" стратегий.

Непосредственно по чертежу находим пару "полезных" стратегий противника B_j и В_к пересекающихся в точке N (если в точке N пересекается более двух стратегий, берём любые две из них). Мы знаем, что если игрок А придерживается своей оптимальной стратегии, то выигрыш не зависит от того, в какой пропорции применяет В свои "полезные" стратегии, следовательно,

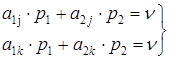(16)

Из этих уравнений и условия р₂=1-р_1, находим р₁, р₂ и цену игры v.

Зная цену игры, можно сразу определить оптимальную стратегию игрока В.

.

Для этого решается, например, уравнение

q_j а _{1 j} + q_k а _{1 k}=v, где q_j + q_k =1.

В случае, когда мы располагаем m стратегиями, а противник - всего двумя, очевидно, задача решается совершенно аналогичным способом; достаточно заметить, что, изменяя знак выигрыша на обратный, можно превратить игрока А из "выигрывающегося" в "проигрывающегося". Можно решить игру и без перемены знака выигрыша; тогда задача решается непосредственно для В, но строится не нижняя, а верхняя граница выигрыша. На границе ищется точка N с минимальной ординатой, которая и есть цена игры v.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: