 |
Закон Стефана-Больцмана. Закони Віна. Формула Планка. Лабораторна робота № 6.1 „Визначення ступеня чорноти нитки лампи розжарювання”.
|
|
|
|
Закон Стефана-Больцмана.
Енергетична світимість абсолютно чорного тіла прямо пропорційна четвертому степеню його абсолютної температури
, (6. 9)
де s = 5, 67·10-8 Дж/(м2·с·К) – стала Стефана-Больцмана.
Для реальних тіл енергетична світимість Rрт при температурі Т може бути виражена як
. (6. 10)
Закони Віна.
Перший закон Віна стверджує, що довжина хвилі, на яку припадає максимум спектральної густини енергетичної світимості, обернено пропорційна абсолютній температурі тіла:
(6. 11)
де b1 = 2, 892·10-3 м·К – стала Віна.
Другий закон Віна вказує, що максимальна спектральна густина енергетичної світимості rlТ прямо пропорційна п’ятому степеню абсолютної температури тіла:
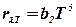, (6. 12)
де b2 = 1, 29·10-5 Вт·м-3·К-5.
Формула Планка.
Фундаментальне значення спектральної густини енергетичної світимості абсолютно чорного тіла одержав в 1900 році німецький фізик М. Планк, зробивши вперше допущення, що тіло випромінює електромагнітні хвилі не безперервно, а окремими квантами (частинами). Енергія кожного кванта пропорційна частоті хвиль:
,
де h = 6, 626·10-34 Дж·с – стала Планка, одна із світових констант. Ця гіпотеза дозволила одержати формулу у вигляді:
, (6. 13)
що дає залежність 
( 
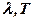), яка повністю збігається з експериментом Кірхгофа. В цій формулі с = 3·108 м/с – швидкість світла в вакуумі, k = 1, 38·10-23 Дж/К – стала Больцмана, і сталі с1, с2 мають точні значення:
, (6. 14)
|
|
|
(6. 15)
Формула (6. 13) і гіпотеза квантів Планка послужили основним поштовхом до розвитку квантової фізики.
Якщо функцію (Т) підставити в (6. 4) і знайти інтеграл, одержимо для енергетичної світимості абсолютно чорного тіла теоретичне значення:
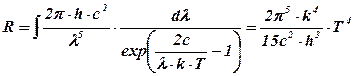. (6. 16)
При цьому стала Стефана-Больцмана одержує точне значення через світові константи:
. (6. 17)
Як наслідок, можна одержати також закон зміщення Віна, досліджуючи функцію (Т) на екстремум. При цьому перша стала Віна b 1 одержує визначення через світові константи:
. (6. 18)
Підставляючи це значення в формулу (6. 12), одержують другий закон Віна, де стала b2 одержує теоретичне визначення через світові константи:
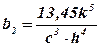. (6. 19)
Таким чином, квантова теорія випромінювання дає всі закони рівноважного теплового випромінювання абсолютно чорного тіла і виражає всі сталі через світові константи: сталу Планка h, сталу Больцмана k і швидкість світла с.
Лабораторна робота № 6. 1 „Визначення ступеня чорноти нитки лампи розжарювання”.
Мета роботи: визначити ступінь (коефіцієнт) почорніння a в формулі (6. 10) і довести аналізом розмірностей і розрахунком чисельних значень s (6. 17), b 1 (6. 18), b2 (6. 19), що ці величини збігаються з експериментально - знайденими коефіцієнтами законів (6. 9, 6. 11, 6. 12) для моделі абсолютно чорного тіла.
Прилади і приладдя: лампа розжарювання, автотрансформатор, амперметр (0, 5 – 1, 0 А) і вольтметр (250 В).
В цьому дослідженні нечорним тілом є вольфрамова нитка лампи розжарювання. При її нагріванні джоулевим теплом 
(де І – струм, U – напруга, t – час), в наближенні, що все тепло випромінюється, виконується співвідношення:
|
|
|
(6. 20)
Опір вольфрамового провідника залежить від температури:
,
де g - відомий температурний коефіцієнт вольфраму. Знехтуємо зміненням лінійних розмірів і перерізу провідника S із зростанням температури: 
Оскільки: T = 273, 15 + t °C і Ro – вимірюється в цій роботі, то:
(6. 21)
Підставляючи T (6. 21) в формулу (6. 20), знайдемо ступінь чорноти:
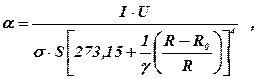(6. 22)
де S – площа бокової поверхні нитки: 
(де d – діаметр нитки, який задається, і l – довжина нитки).
Порядок виконання роботи.
1. Виміряти за допомогою моста постійного струму або омметром опір нитки лампи розжарювання при кімнатній температурі Rо (ця величина може бути задана більш точно при t = 0°C).
Задані сталі: a = 0, 0045 К-1, d = мм, l = мм.
2. Зібрати коло, що приведене на рис. 6. 1.
3. За допомогою автотрансформатора задати в колі напругу в інтервалі 110-200 В через 10-15 В. Виміряти напругу і відповідну силу струму. Одержані результати занести в таблицю:
| № з/п | U, B | I, A | R, Ом | Т, К |
| ... | ||||
4. Розрахувати a по (6. 22) і Т по(6. 21), занести в таблицю:
5. Побудувати залежність a(Т).
6. Визначити відносні похибки на графіку і розрахувати їх.
7. Розрахувати коефіцієнти s (6. 17), b1 (6. 18), b2 (6. 19) і порівняти їх з коефіцієнтами рівнянь (6. 9), (6. 11) і (6. 12), відповідно.
|
|
|
