 |
Порядок розрахунків.. Лабораторна робота № 5.5 „Хвильові властивості світла. Дифракція”.
|
|
|
|
Порядок розрахунків.
1. Розрахувати c2N2 , побудувати графік залежності c2N2 = f(m).
2. Визначити тангенс кута нахилу прямої до осі х і розрахувати радіус кривизни лінзи, використовуючи (5. 65).
3. Провести “найкращу пряму”, використовуючи рекомендації розділу «Вступ». Визначити середнє значення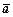 
і його середньоквадратичну похибку.
4. Розрахувати R і DR з одержаного значення а і sа.
5. Порівняти одержані результати графічної і розрахункової обробки даних.
Лабораторна робота № 5. 5 „Хвильові властивості світла. Дифракція”.
Мета роботи : вивчити особливості дифракції на щілині і решітці, як проявлення хвильових властивостей світла, визначити довжину світлової хвилі в дослідах з
   |
дифракційною решіткою.
Явище дифракції виникає коли фронт хвилі частково екранований. Явище дифракції завжди супроводжується явищем інтерференції (інколи кажуть, що дифракція –
це багатопроменева інтерференція світла). Обидва ці явища підтверджують хвильову природу світла. Дифракцією називається відхилення світла від прямолінійного розповсюдження при порушенні фронту хвилі в однорідному середовищі, в наслідок чого світло, яке обводить перешкоду, попадає в область геометричної тіні.
Принцип Гюйгенса-Френеля дозволяє, знаючи напрямок розповсюдження хвилі і положення фронту хвилі в момент часу t, побудувати хвильовий фронт в наступний момент t + Dt. Він стверджує, що, відповідно принципу, кожна точка фронту стає джерелом вторинних хвиль, при цьому вторинні хвилі, будучи когерентними, гасять одне одного у всіх напрямках, окрім напрямку руху початкового фронту. Коливання зберігаються лише на зовнішній обвідній вторинних хвиль. Ця обвідна – новий хвильовий фронт (див. рис. 5. 13).
|
|
|
На рис. 5. 13в видно, як, у відповідності з принципом Гюйгенса-Френеля, фронт хвилі заходить за перешкоду. Дифракцію прийнято розраховувати користуючись зонами Френеля. Зонами Френеля називаються сусідні ділянки фронту, різниця ходу променів з яких до точки спостерігання дорівнює l/2.
1. Дифракція від однієї щілини. Нехай на щілину шириною d падає плоска хвиля. Невідхилений пучок після проходження щілини збирається лінзою, даючи нульовий максимум. Якщо відхилення відбулось на кут j, то тоді, побудувавши фронт хвилі, яка пройшла, можна визначити різницю ходу між променями D = d sinj (рис. 5. 14).
В тому випадку, коли в різниці ходу укладається парне число зон Френеля, вони погасять одне одного (так як різниця ходу від двох зон дорівнює l /2), одержимо мінімум. Якщо число зон Френеля буде непарним, одержимо максимум (більш слабкий порівняно з центральним). Інтенсивність максимумів (0, 1, 2, 3, ... ) буде різною в залежності від віддалення від центру.
Отже, для щілини виконується умова:
- мінімум, (5. 66)
- максимум, k = 1, 2, 3,. (5. 67)
2. Дифракція від двох і більше щілин. При проходженні пучка через дві щілини одержимо два когерентних пучки світла, тому будемо спостерігати:
а) дифракцію світла на кожній із щілин,
б) інтерференцію від пучків, які проходять через кожну із щілин.
З’являться додаткові максимуми і мінімуми, пов’язані з інтерференцією (рис. 5. 15):
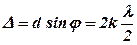максимум, (5. 68)
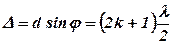мінімум. (5. 69)
При збільшенні числа щілин число додаткових мінімумів буде збільшуватись, при цьому скорочується ширина світлих проміжків. Головні максимуми стають яскравішими, так як збільшується число щілин, частина дифракційних максимумів зникає з-за накладання
|
|
|
інтерференційних мінімумів. При спостереженні в складному світлі максимуми забарвлені (фіолетовий ближче до нульового, ніж червоний).
3. Дифракційна решітка є сукупністю великого числа паралельних смуг, розділених однаковими проміжками. Решітки бувають прозорі і відбивні. Сталою решітки d називається ширина світлого і темного проміжку, якщо N – число штрихів на одиницю довжини, то d = 1/N. При проходженні світла через решітку спостерігається і явище дифракції на кожній щілині, і явище інтерференції між пучками, які пройшли через щілини. Умови максимумів і мінімумів визначаються інтерференцією:
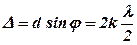максимум, (5. 70)
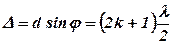мінімум, k = 0, 1, 2, 3 (5. 71)
Дифракція проявляється в тому, що максимумам притаманна різна інтенсивність, при чому різниця тим більша, чим більше період решітки.
Експериментальна установка складається з оптичної лави, на якій закріплена дифракційна решітка, джерела світла, екрана з базовими лініями і щілиною, набору світлофільтрів.
Практичне виконання роботи: Для проведення експерименту слід ввімкнути джерело світла, установити досліджувані світлофільтри, пересуваючи дифракційну решітку вздовж лави, одержати суміщення максимумів 1, 2, 3 порядків з базовими лініями, відмітити відстань z між решіткою і екраном. Дані занести до таблиці:
| k = 1 | k = 2 | |||
| 2х1 = | 2х1 = | |||
| z | x/z | z | x/z | |
| х1 = | ||||
| 2х2 = | 2х2 = | |||
| z | x/z | z | x/z | |
| х2 = | ||||
Вимірювання проводяться тричі для кожного видимого max в спектрі і кожної пари базових ліній (2хі). Стала дифракційної решітки задана.
Порядок розрахунків:
1. З трьох виміряних z для кожної пари базових ліній розрахувати середнє значення і x/z – заповнити таблицю.
2. Максимуми при дифракції на решітці відповідають умові (рис. 5. 16):
d sinj = kl, k = 0, 1, 2, 3… (5. 72)
де sin j » tg j = x/z. Кути при дифракції малі і, як наслідок:
. (5. 73)
|
|
|
З формули витікає, що залежність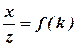 
повинна бути лінійною. Розрахувавши тангенс кута нахилу цієї прямої до горизонтальної осі: 
і знаючи період решітки d, можна знайти довжину хвилі:
. (5. 74)
3. За даними таблиці будується графік залежності 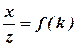і по (5. 74) розраховується l.
4. Введемо позначення: 
Тоді залежність (5. 73) можна переписати як yi = axi. Найкраща пряма yi = axi визначається графічно, з метою визначення середньої величини а.
5. Записати найдений результат з врахуванням похибки, порівняти його з табличними значеннями.
|
|
|
