 |
Лабораторна робота № 8.6 “Визначення коефіцієнта теплопровідності твердого тіла”.
|
|
|
|
Лабораторна робота № 8. 6 “Визначення коефіцієнта теплопровідності твердого тіла”.
Мета роботи: вивчення механізмів теплопровідності твердих тіл, законів Фур’є і Відемана-Франца, визначення коефіцієнта теплопровідності твердого тіла, а у випадку металу – питомої електропровідності за допомогою закона Відемана-Франца.
8. 6. 1. Процеси переносу в твердих тілах.
Твердим тіломназивається тіло, пружне по відношенню до змінення його об’єму і форми. Напам’ятаєм, що газ не має власної форми і об’єму, займаючи весь об’єм посудини. Рідина має свій об’єм, пагано стискається, але не має власної форми, приймаючи форму нижньої частини посудини.
Тверді тіла підрозділяються на кристалічні (істинно тверді), аморфні (дуже переохолоджені рідини з великим коефіцієнтом внутрішнього тертя) і квазіаморфні.
Кристалічні тіла характеризуються впорядкованим розташуванням атомів, іонів або молекул (дальнім порядком на відміну від ближнього порядку в рідинах і аморфних тілах) і переходом при нагріванні в рідкий стан при визначеній температурі плавлення. Вони підрозділяються на монокристали і полікристалічні тіла. Аморфні тіла не мають впорядкованої структури частинок і визначеної температури переходу в рідкий стан, поступово розм’якшуючись при нагріванні. Квазіаморфні тіла при одних умовах поводять себе як кристалічні, а при інших – як аморфні.
Теплопровідність – це один з трьох видів теплопередачі поряд з тепловим випромінюванням і конвекцією. В твердих тілах конвекція неможлива. Тому перенос теплоти здійснюється лише за рахунок теплопровідності. Теплота в твердих тілах передається, перш за все, коливаннями частинок в вузлах кристалічної решітки, які розповсюджуються у вигляді квантованих хвиль – фононів. В металах вона передається також вільними електронами.
|
|
|
Збуджений стан кристалічної решітки при температурі вище дебаївської можна представити як ідеальний газ фононів, які хаотично рухаються в об’ємі тіла. Якщо тіло нагріте рівномірно, то потік енергії, який переноситься фононами в одному напрямку, врівноважується таким самим потоком енергії в протилежному напрямку. Якщо ж два кінці тіла нагріті до різних температур, то потік енергії, який переноситься фононами від більш нагрітого кінця до більш холодного, виявляється більшим, ніж потік в протилежному напрямку. Результуючий тепловий потік Q крізь поперечний переріз S за час t при градієнті температури dT/dx можна розрахувати по формулі Фур’є:
 (8. 46)
(8. 46)
Коефіцієнт пропорціональності К в цій формулі називається коефіцієнтом теплопровідності і характеризує дану речовину, відбиваючи її якості і структуру. Він чисельно дорівнює кількості теплоти, яка пройшла крізь одиницю площі поперечного перерізу тіла за одиницю часу при градієнті температури, який дорівнює одиниці, і вимірюється в Вт/(м·К).
В металах, а також в напівпровідниках є досить велика кількість вільних електронів, які рухаються хаотично і здатні обмінюватись енергією з кристалічною решіткою. Тому в них, окрім фононної теплопровідності, важливу роль відіграє електронна теплопровідність. Механізм її, в принципі, такий самий, що і для фононів: потік електронів, який рухається від більш нагрітого кінця до менш нагрітого, переносить більшу кількість енергії, ніж такий самий потік в протилежному напрямку. Принаймні частина вільних електронів поводиться як ідеальний газ. Тому і для них, і для фононів можна одержати по аналогії із звичайними газами вираз для коефіцієнта теплопровідності у вигляді:
|
|
|
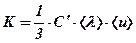 , (8. 47)
, (8. 47)
де  - теплоємність одиниці об’єму фононного або електронного газу,
- теплоємність одиниці об’єму фононного або електронного газу, 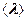 - середня довжина вільного пробігу фононів або електронів,
- середня довжина вільного пробігу фононів або електронів, 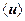 - середньоарифметична швидкість фононів або електронів.
- середньоарифметична швидкість фононів або електронів.
В чистих металах середня довжина вільного пробігу електронів суттєво більша за середню довжину вільного пробігу фононів, яки дуже розсіюються один на одному. Тому в таких металах основну роль відіграє електронна теплопровідність, а фононна складає 1 –2% від електронної. Вказані обставини дозволяють пояснити той факт, що теплопровідність металів набагато більша теплопровідності діелектриків. Між коефіцієнтом теплопровідності ξ і питомою електропровідністю σ металів існує зв’язок, який описується рівнянням (законом) Відемана-Франца:
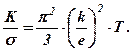 (8. 48)
(8. 48)
Тут 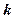 - стала Больцмана,
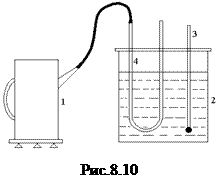
- стала Больцмана,  - заряд електрона,
- заряд електрона,  - температура.
- температура.
 В дуже забруднених металах і невпорядкованих сплавах середня довжина вільного пробігу фононів і електронів приблизно однакова, їхній вклад в теплопровідність одного порядку, а теплопровідність суттєво менша, ніж у чистих металів, хоч і більша, ніж у діелектриків.
В дуже забруднених металах і невпорядкованих сплавах середня довжина вільного пробігу фононів і електронів приблизно однакова, їхній вклад в теплопровідність одного порядку, а теплопровідність суттєво менша, ніж у чистих металів, хоч і більша, ніж у діелектриків.
Знання коефіцієнта теплопровідності дозволяє розрахувати нагрів деталі, яка виготовляється з даного матеріалу, якщо відомі її геометрія і тепловий потік, що відводиться.
В даній роботі коефіцієнт теплопровідності твердого тіла визначається динамічним калориметричним методом.
Вимірювальна установка (рис. 8. 10) містить пароутворювач 1, калориметр 2 з термометром 3, секундомір, штангенциркуль, барометр.
Методика вимірів. Досліджуване тіло у вигляді U-подібної трубки 4, кінці якої виведені крізь кришку калориметра, занурюється в калориметр з водою. Довжину зануреної частини трубки позначимо через l, внутрішній і зовнішній радіуси через r1 і r2 відповідно.
Приєднавши один кінець трубки через штуцер і шланг до пароутворювача, пропускаємо через неї водяну пару, температура якої ТП залежить від атмосферного тиску і приводиться в таблиці. Ту саму температуру має і внутрішня поверхня трубки, в той час як зовнішня поверхня знаходиться при температурі води в калориметрі ТВ. В трубці встановлюється радіальний градієнт температури dT/dr, де r – радіус проміжного циліндричного шару ( r1 < r < r2 ). Градієнт температури направлений всередину трубки, тому тепловий потік направлений назовні. Кількість теплоти, яка за час t пройде крізь трубку до калориметра, можна визначити за допомогою рівняння Фур’є при S=2π rℓ :
|
|
|
 .
.
Ця кількість теплоти змінить температуру води в калориметрі на
 ,
,
де  і
і  - питомі теплоємності води і калориметра,
- питомі теплоємності води і калориметра,  і
і 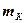 - їхні маси. Перетворимо це диференціальне рівняння до вигляду з розділеними змінними:
- їхні маси. Перетворимо це диференціальне рівняння до вигляду з розділеними змінними:
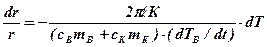 .
.
Інтегруючи його від r1 до r2 і від ТП до ТВ, одержимо вихідний вираз для виводу робочої формули для коефіцієнта теплопровідності ξ :
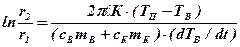 .
.
Таким чином, експериментальна частина роботи зводиться до пропускання пари крізь досліджувану трубку і вимірювання температури води в калориметрі через визначені проміжки часу. Крім того, вимірюються довжина, зовнішній і внутрішній діаметри трубки, маса калориметра і маса калориметра з водою. Відніманням визначається маса води  . По даних вимірювань будується графік залежності температури води від часу ТВ(t) і графічним методом або методом чисельного диференціювання визначається швидкість змінення цієї температури
. По даних вимірювань будується графік залежності температури води від часу ТВ(t) і графічним методом або методом чисельного диференціювання визначається швидкість змінення цієї температури  , яка разом із значенням самої температури ТВ в цей же момент часу і іншими даними підставляється в робочу формулу. Так розраховуються декілька значень коефіцієнта теплопровідності К при декількох значеннях температури.
, яка разом із значенням самої температури ТВ в цей же момент часу і іншими даними підставляється в робочу формулу. Так розраховуються декілька значень коефіцієнта теплопровідності К при декількох значеннях температури.
|
|
|


