 |
Document.write('Натуральные и целые числа'); Натуральные и целые числа
|
|
|
|
Натуральные числа (N).
Натуральные числа (естественные числа) —числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Существуют два подхода к определению натуральных чисел — числа, используемые при:
- перечислении (нумеровании) предметов (первый, второй, третий, …);
- обозначении количества предметов (нет предметов, один предмет, два предмета, …).
- Отрицательные и нецелые (рациональные, вещественные, …) числа натуральными не являются.
Множество всех натуральных чисел принято обозначать знаком 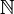 . Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.
. Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.
Простые и составные числа.
Все целые числа (кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называются простыми числами. Числа, имеющие другие делители, называются составными (или сложными) числами. Простых чисел – бесконечное множество. Ниже приведены простые числа, не превосходящие 200:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,
103, 107, 109, 113, 127, 131, 137, 139, 149, 151,
157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
Делитель, кратное. Наибольший общий делитель, наименьшее общее кратное. Признаки делимости на 2,3,5,9,10.
Глава 1. Арифметика
document.write('Натуральные и целые числа'); Натуральные и целые числа

| 
|

| 
|
1.1.2. document.write('Делители и кратные'); Делители и кратные window.top.document.title = "1.1.2. Делители и кратные";
 Для натурального числа b всякое целое число a единственным образом представимо в виде a = bq + r, где 0 ≤ r ≤ |b|.
Для натурального числа b всякое целое число a единственным образом представимо в виде a = bq + r, где 0 ≤ r ≤ |b|.

|
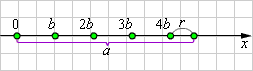
Со времен древних греков известен рисунок, иллюстрирующий доказательство этой теоремы:
|
|
|
 1 1
|
| Рисунок 1.1.2.1 |
Если натуральное число p не делится на натуральное число q, то говорят о делении с остатком. Так, если p – делимое, q – делитель и p > q, то
| p = kq + r, |
где r < q, k – частное, r – остаток. Деление без остатка описывается случаем r = 0.
Если положить, например, q = 5 и r = 1, то получим p = 5k + 1, что представляет собой общую формулу чисел, при делении которых на 5 в остатке получается 1.

|
| Модель 1.1. Деление с остатком |
Напомним, что для натурального числа q всякое натуральное число p единственным образом представимо в виде
| p = kq + r. |
Все натуральные числа имеют, по крайней мере, два натуральных делителя: единицу и самого себя. В случае с единицей эти два делителя совпадают. Все остальные натуральные числа (кроме 1) имеют, по крайней мере, два различных натуральных делителя: единицу и самого себя.

| 
| 
|
| Простыми называются натуральные числа, которые не имеют других натуральных различных делителей, кроме единицы и самого себя. Числа, которые имеют и другие натуральные делители кроме единицы и самого себя, называют составными. | 
| |

| 
| 
|
Число 1 имеет единственный натуральный делитель – самого себя. А значит, согласно данным определениям, оно не является ни простым, ни составным.
 Для того, чтобы доказать, что данное натуральное число простое, достаточно установить, что оно не делится ни на одно из чисел от 2 до
Для того, чтобы доказать, что данное натуральное число простое, достаточно установить, что оно не делится ни на одно из чисел от 2 до 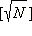 включительно. Если же N делится на одно из таких чисел, то оно составное. включительно. Если же N делится на одно из таких чисел, то оно составное.

|
Более удобный способ отбора составных чисел – решето Эратосфена – предложил в III в. до н. э. древнегреческий математик Эратосфен. Предположим, что нам нужно установить, какие из чисел 2, …, N являются простыми. Выпишем их в ряд и вычеркнем каждое второе число из следующих за числом 2 – все они составные, так как кратны числу 2. Первое из оставшихся невычеркнутыми чисел – 3 – является простым. Вычеркнем каждое третье число из следующих за числом 3; следующее из невычеркнутых чисел – 5 – также будет простым. По тому же принципу вычеркнем каждое пятое число из следующих за числом 5 и вообще каждое k-ое из следующих за числом k. Все оставшиеся невычеркнутыми числа будут простыми.
|
|
|
 Простых чисел бесконечно много.
function changeProof(proofobj) { if (proofobj.style.display=='none') {proofobj.style.display='inline'} else {proofobj.style.display='none'} } Доказательство
Простых чисел бесконечно много.
function changeProof(proofobj) { if (proofobj.style.display=='none') {proofobj.style.display='inline'} else {proofobj.style.display='none'} } Доказательство
|
Приведем список простых чисел в пределах первой сотни:
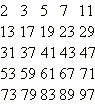
|
Глядя на эту таблицу, можно убедиться в том, что простые числа распределены в натуральном ряду неравномерно. Существует расположенные рядом простые «числа-близнецы» (2 и 3, 3 и 5, 17 и 19, 41 и 43 и т. д.). С другой стороны, есть бесконечно длинные отрезки натурального ряда, на которых простых чисел нет вообще (так, среди последовательных чисел x + 2, x + 3, x + 4, …, x + k, где x = 1 · 2 · … · (k – 1) · k, нет ни одного простого).
Обозначим через π (n) число простых чисел, меньших n. Немецкий математик Леонард Эйлер доказал, что отношение 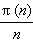 при больших n сколько угодно близко приближается к нулю. Позже математики доказали, что для больших n число
при больших n сколько угодно близко приближается к нулю. Позже математики доказали, что для больших n число 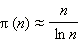 (с понятием логарифма мы познакомимся позже). Также доказано, что для натурального числа n в промежутке [n; 2n] всегда найдется хотя бы одно простое число.
(с понятием логарифма мы познакомимся позже). Также доказано, что для натурального числа n в промежутке [n; 2n] всегда найдется хотя бы одно простое число.
Одно дело – знать, что простых чисел бесконечно много, и совсем другое – доказать, что данное число n является простым. В 2005 году было доказано, что число (230402457 – 1) простое; оно содержит в своей записи более 900 тысяч цифр.
Определить, является ли большое число простым, очень непросто. В настоящее время эта проблема решается при помощи ЭВМ, однако даже на самых быстрых из современных ЭВМ доказательство того, что число, состоящее из нескольких сотен цифр, является простым, может занять месяцы и годы. На сложности определения простоты чисел основаны современные механизмы шифрования данных.
|
|
|
Справедлива фундаментальная теорема о разложении числа на простые множители.
 Любое натуральное число, отличное от 1, единственным образом разлагается в произведение простых чисел с точностью до порядка сомножителей.
Любое натуральное число, отличное от 1, единственным образом разлагается в произведение простых чисел с точностью до порядка сомножителей.

|
Если требуется разложить небольшое число на простые множители, то эти простые множители можно угадать. Для того, чтобы разложить большое число на простые множители, используют следующий приём. Применяют признаки делимости и запись в столбик, причём делимое располагается слева от вертикальной черты, а делители – справа.

|
| Модель 1.2. Разложение на простые множители |
Пример 1
Разложить на простые множители число 92820.
function changeDecision(proofobj, proofname) { if (proofobj.style.display=='none') { proofobj.style.display='inline'; proofname.innerHTML='Решение'; } else { proofobj.style.display='none'; proofname.innerHTML='Показать решение'; } } Показать решение
Воспользуемся записью в столбик.
Значит, Ответ. |
Для того чтобы не писать несколько раз одно и то же число в разложении на простые множители, можно записать коротко 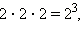
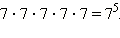 И вообще, если какой-то множитель a встречается n раз, то записывают коротко:
И вообще, если какой-то множитель a встречается n раз, то записывают коротко: 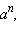 то есть
то есть 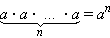 .
.

| 
| 
|
Выражение 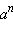 называется степенью с натуральным показателем. Ясно, что называется степенью с натуральным показателем. Ясно, что 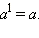 Число a называется основанием степени, а n – показателем степени. Третья степень числа называется кубом, вторая – квадратом. Первой степенью называется само число a. Число a называется основанием степени, а n – показателем степени. Третья степень числа называется кубом, вторая – квадратом. Первой степенью называется само число a.
| 
| |

| 
| |
Извлечением корня называется нахождение основания степени по степени и её показателю. Данная степень называется подкоренным числом, данный показатель называется показателем корня, искомое основание степени называется корнем. Например, так как 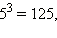 то пишут:
то пишут: 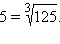 Здесь 5 – корень, 3 – показатель корня, 125 – подкоренное выражение. Корень второй степени называется квадратным корнем, корень третьей степени – кубическим. Принято опускать показатель корня, если корень является квадратным:
Здесь 5 – корень, 3 – показатель корня, 125 – подкоренное выражение. Корень второй степени называется квадратным корнем, корень третьей степени – кубическим. Принято опускать показатель корня, если корень является квадратным:  поскольку
поскольку 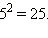
|
|
|
Общим делителем нескольких чисел называется число, являющееся делителем каждого их этих чисел. Среди всех делителей всегда есть наибольший. Такой делитель называется наибольшим общим делителем (обозначается НОД). Так, например, числа 16, 24, 32 имеют наибольший общий делитель – число 8. Этот факт коротко записывается так: НОД (16, 24, 32) = 8.
Если данные числа небольшие, то наибольший общий делитель можно легко угадать. Если же даны большие числа, то НОД можно найти разложением чисел на простые множители и выписыванием тех множителей, которые входят во все данные числа. Затем каждый такой множитель следует взять с наименьшим показателем, с которым он входит во все данные числа, после чего нужно произвести умножение.

|
| Модель 1.3. Наибольший общий делитель |
Пример 2
Пусть даны числа 1080 и 8100. Найти НОД (1080, 8100).
function changeDecision(proofobj, proofname) { if (proofobj.style.display=='none') { proofobj.style.display='inline'; proofname.innerHTML='Решение'; } else { proofobj.style.display='none'; proofname.innerHTML='Показать решение'; } } Показать решение
Выпишем все простые делители числа 1080:
Выпишем теперь все простые делители числа 8100:
Таким образом,
(//// решение/// Выпишем все простые делители числа 1080:
Выпишем теперь все простые делители числа 8100:
Таким образом, Ответ. | ||||||
Если числа a и b таковы, что НОД (a, b) = 1, то числа a и b называют взаимно простыми. Например, числа 21 и 26 являются взаимно простыми, хотя каждое из них – составное.
Общим кратным нескольких чисел называется число, являющееся кратным каждого из них. Например, числа 14, 18, 7 имеют общее кратное число 252, однако число 126 тоже является общим кратным этих чисел. Среди всех общих кратных всегда есть наименьшее, которое называется наименьшим общим кратным (обозначается НОК). В нашем примере наименьшим общим кратным перечисленных чисел будет число 126. Кратко этот факт записывается так: НОК (14, 18, 7) = 126.
Если числа небольшие, то наибольшее общее кратное можно легко угадать. Если же даны большие числа, то НОК можно найти разложением чисел на простые множители и выписыванием тех множителей, которые входят хотя бы в одно из данных чисел. После этого каждый такой множитель нужно взять с наибольшим показателем, с которым он входит во все данные числа. Затем следует произвести умножение.

|
| Модель 1.4. Наименьшее общее кратное |
Пример 3
Пусть даны числа 1080 и 8100. Найти НОК (1080, 8100).
|
|
|
Показать решение
Выпишем все простые делители числа 1080:
Выпишем теперь все простые делители числа 8100:
Таким образом,
Ответ. НОК (1080, 8100) = 16200. |
(////Решение/////
Воспользуемся записью в столбик.
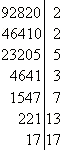 2 2
|
Значит, 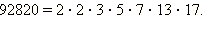
Ответ. 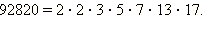
////Решение///)
Целые числа (Z)
Множество целых чисел (от ср.-лат. cifra от араб. صفر (ṣifr) «пустой, нуль») — 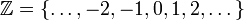 , определяется как замыкание множества натуральных чисел
, определяется как замыкание множества натуральных чисел 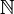 относительно арифметических операций сложения (+) и вычитания (-). Таким образом, сумма, разность и произведение двух целых чисел дает снова целые числа. Оно состоит из натуральных чисел (1, 2, 3), чисел вида -n (
относительно арифметических операций сложения (+) и вычитания (-). Таким образом, сумма, разность и произведение двух целых чисел дает снова целые числа. Оно состоит из натуральных чисел (1, 2, 3), чисел вида -n (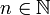 ) и числа нуль.
) и числа нуль.
Необходимость рассмотрения целых чисел продиктована невозможностью (в общем случае) вычесть из одного натурального числа другое. Целые числа являются кольцом относительно операций сложения и умножения.
Алгебраические свойства
 не замкнуто относительно деления двух целых чисел (например, 1/2). Следующая таблица иллюстрирует несколько основных свойств сложения и умножения для любых целых a, b и c.
не замкнуто относительно деления двух целых чисел (например, 1/2). Следующая таблица иллюстрирует несколько основных свойств сложения и умножения для любых целых a, b и c.
| сложение | умножение | |
| замкнутость: | a + b — целое | a × b — целое |
| ассоциативность: | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| коммутативность: | a + b = b + a | a × b = b × a |
| существование нейтрального элемента: | a + 0 = a | a × 1 = a |
| существование противоположного элемента: | a + (− a) = 0 | a ≠ ±1 ⇒ 1/ a не является целым |
| дистрибутивность умножения относительно сложения: | a × (b + c) = (a × b) + (a × c) |
На языке абстрактной алгебры первые пять вышеперечисленных свойств сложения говорят о том, что  является абелевой группой относительно бинарной операции сложения, и, следовательно, также циклической группой, так как каждый ненулевой элемент
является абелевой группой относительно бинарной операции сложения, и, следовательно, также циклической группой, так как каждый ненулевой элемент  может быть записан в виде конечной суммы 1 + 1 + … 1 или (−1) + (−1) + … + (−1). Фактически,
может быть записан в виде конечной суммы 1 + 1 + … 1 или (−1) + (−1) + … + (−1). Фактически,  является единственной бесконечной циклической группой по сложению в силу того, что любая бесконечная циклическая группа изоморфна группе
является единственной бесконечной циклической группой по сложению в силу того, что любая бесконечная циклическая группа изоморфна группе 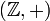 .
.
Первые четыре свойства умножения говорят о том, что  — коммутативный моноид по умножению. Однако стоит заметить, что не каждое целое имеет противоположное по умножению, например, нет такого x из
— коммутативный моноид по умножению. Однако стоит заметить, что не каждое целое имеет противоположное по умножению, например, нет такого x из  , что 2x = 1, так как левая часть уравнения чётна, а правая нечётна. Из этого следует, что
, что 2x = 1, так как левая часть уравнения чётна, а правая нечётна. Из этого следует, что  не является группой по умножению, а также не является полем. Наименьшее поле, содержащее целые числа, — множество рациональных цисел (
не является группой по умножению, а также не является полем. Наименьшее поле, содержащее целые числа, — множество рациональных цисел (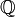 ).
).
Совокупность всех свойств таблицы означает, что  является коммутативным кольцом с единицей относительно сложения и умножения.
является коммутативным кольцом с единицей относительно сложения и умножения.
Обычное деление не определено на множестве целых чисел, но определено так называемое деление с остатком: для любых целых a и b,  , существует единственный набор целых чисел q и r, что a = bq + r и
, существует единственный набор целых чисел q и r, что a = bq + r и 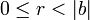 , где | b | — абсолютная величина (модуль) числа b. Здесь a — делимое, b — делитель, q — частное, r — остаток. На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.
, где | b | — абсолютная величина (модуль) числа b. Здесь a — делимое, b — делитель, q — частное, r — остаток. На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.
Рациональные числа (Q), их сложение, вычитание, умножение и деление. Сравнение рациональных чисел.
Рациональные числа – это числа, которые можно представить в виде дроби 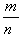 , где m и n – целые числа, n? 0. Пример:
, где m и n – целые числа, n? 0. Пример:  ;
; 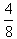 ;
; 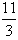 ; 1,01; 12 и т.д. Все целые числа являются рациональными.
; 1,01; 12 и т.д. Все целые числа являются рациональными.
Действительно, любое целое число n можно представить в виде дроби 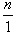 . Например, целое число
. Например, целое число
18 – это  .
.
Две дроби  считаются равными, если
считаются равными, если 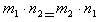 .
.
Пример: 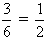 =, так как 3 • 2 = 6 • 1.
=, так как 3 • 2 = 6 • 1.
Очевидно, что дроби 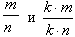 равны. На этом свойстве основано сокращение дробей. Для того чтобы сократить дробь, находим общий делитель числителя и знаменателя и на этот делитель делим числитель и знаменатель - полученная дробь будет равна исходной.
равны. На этом свойстве основано сокращение дробей. Для того чтобы сократить дробь, находим общий делитель числителя и знаменателя и на этот делитель делим числитель и знаменатель - полученная дробь будет равна исходной.
Пример: Сократить дробь 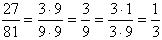 .
.
Над рациональными числами операции сложения, умножения и деления определены следующим образом:
1. Операция сложения:  .
.
Пример: 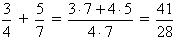 .
.
2. Операция умножения:  .
.
Пример:  .
.
3. Операция деления:  , то есть, делитель «переворачиваем»
, то есть, делитель «переворачиваем»
Пример:  .
.
При сравнении рациональных чисел применяют следующие правила:
1. Всякое положительное рациональное число всегда больше всякого отрицательного рационального числа.
2. Если два числа 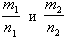 положительны, то число
положительны, то число 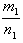 больше
больше 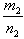 , если
, если  , для отрицательных - наоборот.
, для отрицательных - наоборот.
Пример:  , так как 3 • 6 > 5 • 2.
, так как 3 • 6 > 5 • 2.
|
|
|




 а
а 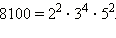 Значит,
Значит,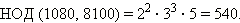
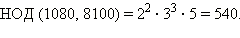 ////решение////)Ответ.
////решение////)Ответ.  а
а