Изображение чисел на прямой. Модуль действительного числа, его геометрический смысл.

Числовая прямая, числовая ось, - это прямая на которой изображаются действительные числа. На прямой выбирают начало отсчета – точку О (точка О изображает 0) и точку L, изображающую единицу. Точка L обычно стоит справа от точки О. Отрезок ОL называют единичным отрезком.

Точки, стоящие справа от точки О изображают положительные числа. Точки стоящие слева от точки. О, изображают отрицательные числа. Если точка Х изображает положительное число х, то расстояние ОХ = х. Если точка Х изображает отрицательное число х, то расстояние ОХ = - х.

Число, показывающее положение точки на прямой, называется координатой этой точки.

Точка V изображенная на рисунке имеет координату 2, а точка H имеет координату -2,6.

Модулем действительного числа называется расстояние от начала отсчета до точки, соответствующей этому числу. Обозначают модуль числа х, так: | х |. Очевидно, что | 0 | = 0.

Если число х больше 0, то | х | = х, а если х меньше 0, то | х | = - х. На этих свойствах модуля, основано решение многих уравнений и неравенств с модулем.

Пример: Решить уравнение | х – 3 | = 1.

Решение: Рассмотрим два случая – первый случай, когда х -3 > 0, и второй случай, когда х - 3 0.

1. х - 3 > 0, х > 3.

В этом случае | х – 3 | = х – 3.

Уравнение принимает вид х – 3 = 1, х = 4. 4 > 3 – удовлетворят первому условию.

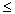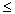2. х -3 0, х 3.

В этом случае | х – 3 | = - х + 3

Уравнение принимает вид х + 3 = 1, х = - 2. -2 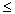3 – удовлетворят второму условию.

Ответ: х = 4, х = -2.

Числовые выражения.

Числовое выражение – это совокупность одного или нескольких чисел и функций, соединенных знаками арифметических операций и скобками.
Примеры числовых выражений:

Значением числового выражения является число.
Операции в числовом выражении выполняются в следующей последовательности:

1. Действия в скобках.

2. Вычисление функций.

3. Возведение в степень

4. Умножение и деление.

5. Сложение и вычитание.

6. Однотипные операции выполняются слева на право.

Так значением первого выражения будет само число 12,3
Для того чтобы вычислить значение второго выражения, действия будем выполнять в следующей последовательности:

1. Выполним действия в скобках в следующей последовательности - сначала 2 возведем в третью степень, затем от полученного числа отнимем 11:

3 • 4 + (23 - 11) = 3 • 4 + (8 - 11) = 3 • 4 + (-3)

2. Умножим 3 на 4:

3 • 4 + (-3) = 12 + (-3)

3. Выполним последовательно операции слева направо:

12 + (-3) = 9.
Выражение с переменными – это совокупность одного или нескольких чисел, переменных и функций, соединенных знаками арифметических операций и скобками. Значения выражений с переменными зависят от значений, входящих в него переменных. Последовательность выполнения операций здесь та же, что и для числовых выражений. Выражения с переменными иногда бывает полезно упрощать, выполняя различные действия – вынесение за скобки, раскрытие скобок, группировки, сокращение дробей, приведение подобных и т.д. Так же для упрощения выражений часто используют различные формулы, например, формулы сокращенного умножения, свойства различных функций и т. д.

Алгебраические выражения.

Алгебраическим выражением называется одна или несколько алгебраических величин (чисел и букв), соединенных между собой знаками алгебраических действий: сложения, вычитания, умножения и деления, а также извлечения корня и возведения в целую степень (причём показатели корня и степени должны обязательно быть целыми числами) и знаками последовательности этих действий (обычно скобками различного вида). Количество величин, входящих в алгебраическое выражение должно быть конечным. ^[1]

Пример алгебраического выражения:

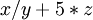
«Алгебраическое выражение» — понятие синтаксическое, то есть нечто является алгебраическим выражением тогда и только тогда, когда подчиняется некоторым грамматическим правилам (см. Формальная грамматика). Если же буквы в алгебраическом выражении считать переменными, то алгебраическое выражение обретает смысл алгебраической функции.