|
Равенства и неравенства алгебраических выражений. Многочлены.
|
|
|
|
Алгебраические дроби. Формулы сокращенного умножения.
Степень с натуральным и рациональным показателем. Арифметический корень.
Тождественные преобразования алгебраических выражений
Определение. Алгебраическим выражением называется выражение, получаемое из постоянных и переменных при помощи операций сложения, вычитания, умножения, деления, возведения в целую степень и извлечения корня.
Примеры алгебраических выражений:

Определение. Областью допустимых значений (сокращенно ОДЗ) алгебраического выражения E (x 1, x 2,..., xn) (D (E)) называется множество всех наборов (x 1, x 2,..., xn), для которых выражение E (x 1, x 2,..., xn) имеет смысл.
Например, ОДЗ выражения 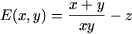 является D (E) = {(x, y) | x Î R, y Î R, xy ≠ 0}, ОДЗ выражения
является D (E) = {(x, y) | x Î R, y Î R, xy ≠ 0}, ОДЗ выражения 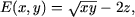 является множество {(x, y, z) | x, y, z Î R, xy ≥ 0}.
является множество {(x, y, z) | x, y, z Î R, xy ≥ 0}.
Определение. Алгебраические выражения E 1 и E 2 называются тождественно равными на множестве M Ì D (E 1)Ç D (E 2), если при любых значениях переменных из M соответствующие числовые значения этих выражений равны.
Например, 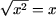 на множестве [0;+¥),
на множестве [0;+¥),  на множестве (-¥;0],
на множестве (-¥;0],  на множестве R \{-1}, (x + y)2 = x 2 + 2 xy + y 2 на множестве {(x, y) | x Î R, y Î R }.
на множестве R \{-1}, (x + y)2 = x 2 + 2 xy + y 2 на множестве {(x, y) | x Î R, y Î R }.
Определение. Тождественным преобразованием алгебраического выражения на множестве M Í D (E) называется замена этого выражения на тождественно равное ему на множестве M
Замечание. Отметим, что иногда опускают множество, на котором алгебраические выражения тождественно равны, имея при этом ввиду их тождественное равенство на пересечении областей допустимых значений.
Например,

При выполнении тождественных преобразований оказываются полезными следующие формулы.
I. Формулы сокращенного умножения
- (a ± b)2 = a 2 ± 2 ab + b 2,
- (a ± b)3 = a 3 ± 3 a 2 b + 3 ab 2 ± b 3,
- a 2 - b 2 = (a - b)(a + b),
- a 3 ± b 3 = (a ± b)(a 2
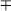 ab + b 2).
ab + b 2).
Эти формулы получаются как следствия из более общих формул:
|
|
|
- an - bn = (a - b)(an -1 + an -2 b +... + abn -2 + bn -1) (n Î N),
- a 2 n +1 + b 2 n +1 = (a + b)(a 2 n - a 2 n -1 b +... - ab 2 n -1 + b 2 n ) (n Î N),
- (бином Ньютона)
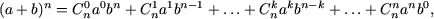
где n Î N,  n! = 1·2·3·...· n, 0! = 1.
n! = 1·2·3·...· n, 0! = 1.
II. Свойства степеней
Следующие свойства справедливы для любых положительных чисел a и b и любых действительных чисел a и b.
- a 0 = 1;
- a a + b = a a · a b;
-
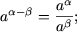
- (a a)b = a ab;
- (ab)a = a a · b a;
-
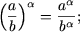
-
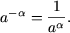
Замечание 1. Отметим, что отрицательные числа также можно возводить в некоторые степени (целые и, более общо, рациональные вида 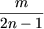 где m - целое, n - натуральное).
где m - целое, n - натуральное).
Замечание 2. 0a = 0, для любого a > 0.
III. Свойства радикалов
-

-
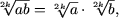 если a ≥ 0, b ≥ 0, k Î N,
если a ≥ 0, b ≥ 0, k Î N, -
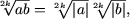 если ab ≥ 0, k Î N.
если ab ≥ 0, k Î N. -

-
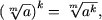 где a ≥ 0, если m - четно, a Î R, если m - нечетно.
где a ≥ 0, если m - четно, a Î R, если m - нечетно. -
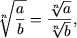 где a ≥ 0, b > 0, n - четно или b ≠ 0, a Î R, если n - нечетно.
где a ≥ 0, b > 0, n - четно или b ≠ 0, a Î R, если n - нечетно. -
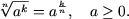
-
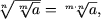 где a ≥ 0, если m - четно или n четно, a Î R, если m · n - нечетно.
где a ≥ 0, если m - четно или n четно, a Î R, если m · n - нечетно. -

-
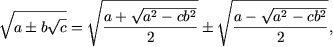 где a > 0, b > 0, c > 0 и a 2 ≥ b 2 c.
где a > 0, b > 0, c > 0 и a 2 ≥ b 2 c.
Пример 1. Определить ОДЗ алгебраических выражений:
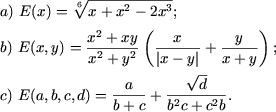
Решение. a) ОДЗ данного выражения определяется из неравенства x + x 2 - 2 x 3 ≥ 0, которое решаем при помощи метода интервалов:
x + x 2 - 2 x 3 ≥ 0 Û x (1 + x - 2 x 2) ≥ 0 Û x (2 x + 1)(1 - x) ≥ 0 Û x Î (-¥;-1/2]È[0;1].
Таким образом, D (E) = (-¥;-1/2]È[0;1].
b) Отметим, что выражение имеет смысл тогда и только тогда, когда

| x 2 + y ≠ 0, |
| | x - y | ≠ 0, | |
| x + y ≠ 0, |
откуда следует, что D (E) = {(x, y) | x ≠ y, x ≠ - y }.
c) Так как знаменатель дроби должен быть отличен от нуля, а корень второй степени существует только из неотрицательных выражений, то для определения ОДЗ получим систему
| Û |
| Û |
|
Таким образом, ОДЗ исходного выражения равна {(a, b, c, d) | b + c ≠ 0, b ≠ 0, c ≠ 0, d ≥ 0}.
Логарифмы, их свойства.
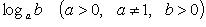 - логарифм числа b по основанию a.
- логарифм числа b по основанию a.
Основное логарифмическое тождество: 
|
|
|
 - десятичный логарифм (логарифм по основанию 10):
- десятичный логарифм (логарифм по основанию 10): 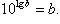
 - натуральный логарифм (логарифм по основанию e):
- натуральный логарифм (логарифм по основанию e): 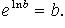
Переход от одного основания к другому:
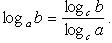
В частности, 
 (
(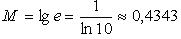 - модуль перехода от натуральных логарифмов к десятичным).
- модуль перехода от натуральных логарифмов к десятичным).
Свойства логарифмов (u, v >0):

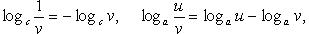
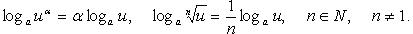
Тригонометрия. Углы и их измерение. Синус, косинус, тангенс, котангенс угла.
|
|
|