 |
Иррациональные числа. Сравнение иррациональных и рациональных чисел.
|
|
|
|
Иррациональные числа. Числа целые, дробные, десятичные конечные и десятичные периодические носят общее название рациональных чисел; десятичные бесконечные дроби непериодические называются иррациональными числами2). Первые служат мерою величин, соизмеримых с единицею, вторые—мерою величин, несоизмеримых с единицею.
Иррациональное число считается известным (или данным), если указан способ, посредством которого можно находить любое число его десятичных знаков.
Два иррациональных числа (как и два рациональных) считаются равными, если они произошли от измерения одною и тою же единицею двух равных величин; из двух неравных чисел то считается большим, которое произошло от измерения большей величины. Две равные величины, конечно, должны содержать в себе одинаковое число целых единиц, одинаковое число десятых долей, одинаковое число сотых долей и т. п., поэтому равные иррациональные числа должны быть выражены одинаковыми цифрами3). Большая же величина должна содержать в себе большее число целых или — при равенстве целых—большее число десятых, или — при равенстве целых и десятых — большее число, сотых и т. д. Напр., число 2,745037... больше числа 2,745029..., так как в первом 6-я цифра выражает число большее, чем 6-я цифра во втором, при тождественности всех предыдущих цифр.
Иррациональные числа могут быть положительными и отрицательными, смотря по тому, измеряют ли они величины, считаемые положительными, или величины, считаемые отрицательными.
186. Приближенные значения иррационального числа. Пусть нам дано какое-нибудь иррациональное число α 4), т. е. пусть указан способ, посредством которого мы можем получить сколько угодно цифр числа α (этим способом может быть, напр., то правило, посредством которого мы находим приближенные квадратные корни с точностью до 1/10 до 1/100 до 1/1000 и т. д.). Положим, мы нашли такие 5 цифр числа α:
|
|
|
α = 1,4142...
Возьмем из этих цифр несколько первых, напр, цифры 1,41, а остальные отбросим. Тогда мы получим приближенное значение числа α, причем это значение будет с недостатком, так как 1,41 < α. Если последнюю из удержанных нами цифр увеличим на 1, т. е. вместо 1,41 возьмем 1,42, то получим тоже приближенное значение числа α, но с избытком. Обыкновенно из двух приближенных значений, из которых одно с недостатком, другое с избытком, берут значение с недостатком, если первая из отброшенных цифр менее 5, и значение с избытком, если эта цифра больше 5.
187. Определение действий над иррациональными числами. Пусть α и β будут какие-нибудь данные положительные иррациональные числа. Если эти числа даны, то это значит, что мы можем найти их приближенные значения с любою точностью. Пусть, напр., приближенные значения чисел α и β, взятые с недостатком, будут такие (мы берем приближенные значения √3 и √2):
| до 0,1 | до 0,01 | до 0,001 | до 0,0001 | |
| для числа α..... | 1,7 | 1,73 | 1,732 | 1,7320 |
| для числа β..... | 1,4 | 1,41 | 1,414 | 1,4142 |
(Соответствующие приближенные значения с избытком получаются из этих чисел посредством усиления последнего десятичного знака на 1.)
Тогда: а) сложить α и β значит найти число, которое было бы
| больше каждой из сумм: 1,7 + 1,1.... =3,1 1,73 + 1,41... =3,14 1,732+1,414...=3,146 1,7320+1,4142.. =3,1462 | и меньше каждой из сумм: 1,8+1,6.... =3,3 1,74+1,42... =3,16 1,733 + 1,415.. =3,146 1,7321 + 1,4143..=3,1464 |
т. е. сложить числа α и β — значит найти такое третье число, которое было бы больше суммы любых приближенных их значении, взятых с недостатком, но меньше суммы любых приближенных значении, взятых с избытком.
б) Беря приближенные значения чисел α и β, указанные сейчас, мы можем сказать, что произведение α β есть число, которое
|
|
|
| больше каждого из произв.: 1,7•1,4......... =2,38 1,73 • 1,41.......=2,4393 1,732•1,114......=2,449048 1,7320 • 1,1142...=2,44939440 | и меньше каждого из произв.: 1,8•1,5..........=2,70 1,74 • 1,42.......=2,4708 1,733•1,415......=2,452195 1,7321 •.1,4143...=2,44970903 |
т. е. перемножить числа α и β — значит найти такое третье число, которое было бы больше произведения их любых приближенных значений, взятых с недостатком, но меньше произведения их любых приближенных значений, взятых с избытком.
в) Возвысить иррациональное число α во вторую, третью, четвертую и т. д. степени — значит найти произведение, составленное из двух, трех, четырех и т. д. сомножителей, равных α.
г) Обратные действия определяются для иррациональных чисел так же, как и для рациональных; так, вычесть из числа α число β значит найти такое число х, чтобы сумма β + х равнялась α, и т. п.
Если одно из чисел α или β будет рациональное, то в указанных определениях прямых действий вместо приближенных значений такого числа можно брать точное число.
Произведение иррационального числа на нуль принимается, как и для чисел рациональных, равным нулю.
Действия над отрицательными иррациональными числам и производятся согласно правилам, данным для рациональных отрицательных чисел.
При более обстоятельном рассмотрении можно установить, что действия над иррациональными числами обладают теми же свойствами, какие принадлежат действиям над числами рациональными; напр., сумма и произведение обладают свойствами переместительным и сочетательным; произведение и деление, кроме того, обладают еще распределительным свойством. Свойства, выражаемые неравенствами, также сохраняются у чисел иррациональных; так, если α > β, то α + γ > β, αγ > βγ (если γ > 0) и αγ < βγ (если γ < 0) и т. п.
Действительные числа (R), их представление в виде десятичных дробей.
Еще древние греки обнаружили, что не всегда длину точно заданного отрезка можно выразить с помощью рационального числа. Например, если задан квадрат, длины сторон которого имеют длину, заданную рациональным числом, то какова длина его диагонали? Диагональ можно нарисовать точно, но невозможно выразить ее длину с помощью рационального числа. Такие отрезки называли несоизмеримыми. Однако, греками была разработана теория отношения отрезков, учитывая, что они могут быть несоизмеримы.
|
|
|
Современная математика использует в этом случае понятие иррационального числа.
Иррациональное число – число, которое не может быть представлено ни в виде дроби с целым числителем и знаменателем, ни в виде бесконечной периодичной десятичной дроби. Иррациональные числа могут быть представлены только бесконечными непериодическими дробями.
Примеры иррациональных чисел:
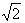 - это иррациональное число.
- это иррациональное число. 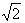 = 1, 41…
= 1, 41…
е = 2,718281828459045…
Действительное числа, вещественное число – это любое рациональное или иррациональное число.
Примеры действительных чисел: 3/5; 1,8; 7,121212…; 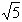 ….
….
|
|
|


