 |
Критерии оценки экзаменационной работы в виде набора контрольных заданий
|
|
|
|
Оценка 5 (отлично) ставится за работу, выполненную полностью без ошибок и недочётов; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Оценка 4 (хорошо) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Оценка 3 (удовлетворительно) ставится, если обучающийся правильно выполнил не менее 2/3 всей работы или допустил не более одной грубой ошибки и двух недочётов, не более одной грубой и одной не грубой ошибки, не более трёх негрубых ошибок, одной негрубой ошибки и трёх недочётов, при наличии четырёх-пяти недочётов.
Оценка 2 (неудовлетворительно) ставится, если число ошибок и недочётов превысило норму для оценки 3 или правильно выполнено не менее 2/3 всей работы; допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере
КЛЮЧ
| № | 1 вариант | 2 вариант | 3 вариант | 4 вариант |
| 1. | -3786,7 | 20 | 1,03 | 1,55 |
| 2. | 1 | 1 | 1 | 2 |
| 3. | 1 | 4 | 2 | 2 |
| 4. | -5;3 | 6 | 0,5;1 | 3;6 |
| 5. | 412 | 132 | 4 | 1 |
| 6. | 4 | 521 | -847 | 128 |
| 7. | 31 | 1,5 | 0,4 | 84 |
| 8. | 4 | 3 | 1 | 2 |
| 9. | 95 | 11,25 | 80 | 33 |
| 10. | 144 | 30 | 4 | 6 |
| 11. | 2688 | 50 | 156 | 270 |
| 12. | 2 | 28 | 52 | 58 |
| 13. | 1;3 | 3 | 2;3;4 | 13|31|1;3|1,3 |
| 14. | 4 | 4 | 4 | 2 |
| 15. | 16 | 756 | 1;3|13|1; 3 | 50000 |
| 16. | 4553000000 | 10 | 16000000 | 9 |
| 17. | 105 | 3,5 | 1440 | 15 |
| 18. | 1 | 3 | 4 | 3 |
| 19. | 0,6 | 0,42 | 0,0625 | 0,0625 |
| 20. | 5 | 0,98 | 26500 | 88000 |
| 21. | -8:-5 | 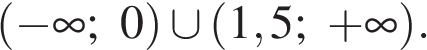
| -1;0;5 | (3; −4) |
| 22. | 61,6 | 5 | 16 км/ч | 220 |
| 23. | 2,6 | 
| 2/3;1;2 | (0;5) |
| 24. | 3 | 8 | 16 | 102°, 24°, 54° |
| 25. | ||||
| 26. | 
| 3,2 | 9 | 
|
25. 1 вариант.
|
|
|
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Решение.

Поскольку четырёхугольник ABCD вписанный, сумма углов BAD и BCD равна 180°.
Следовательно,
∠ MCB = 180° − ∠ BCD = ∠ BAD.
Получаем, что в треугольниках MBC и MDA углы MCB и MAD равны, угол M общий, следовательно, эти треугольники подобны.
25. 2 вариант.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.
Решение.
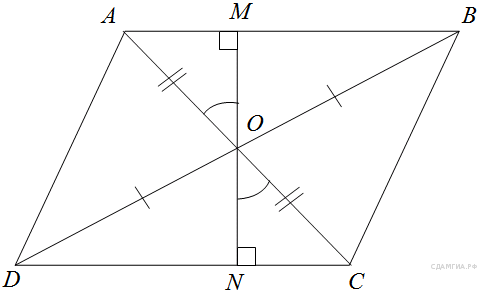 Проведём высоту
Проведём высоту 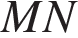 так, чтобы она проходила через точку
так, чтобы она проходила через точку  Углы
Углы  и
и  равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно,
равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно,  Рассмотрим треугольники
Рассмотрим треугольники  и
и  , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки
, они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки 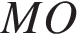 и
и  . Таким образом,
. Таким образом, 
Площадь параллелограмм равна  а площадь треугольника
а площадь треугольника 
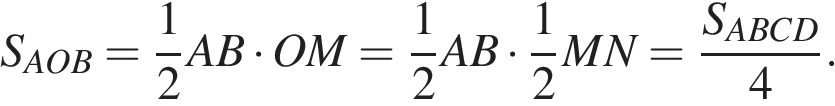
25. 3 вариант.
Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.
Решение.
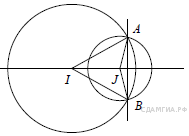 Точка I равноудалена от A и B, поэтому она лежит на серединном перпендикуляре к отрезку AB. То же можно сказать и о J. Значит IJ — серединный перпендикуляр к AB.
Точка I равноудалена от A и B, поэтому она лежит на серединном перпендикуляре к отрезку AB. То же можно сказать и о J. Значит IJ — серединный перпендикуляр к AB.
25. 4 вариант.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD = 10. Докажите, что треугольники CBD и ADB подобны.
Решение.
 Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках  и
и 
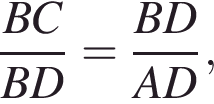 следовательно, эти треугольники подобны по двум парам подобных сторон и углу между ними.
следовательно, эти треугольники подобны по двум парам подобных сторон и углу между ними.
|
|
|
Контрольная работа по математике
Специальность 09.02.03 Программирование в компьютерных системах
1. Вычислить предел:
1). 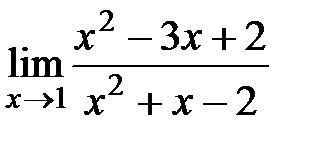 Ответ:
Ответ:
2). 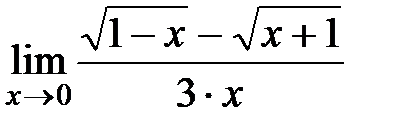 Ответ:
Ответ:
3)  Ответ
Ответ
4). 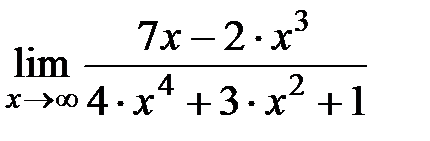 Ответ
Ответ
5). 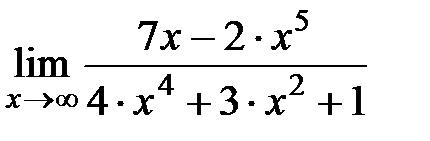 Ответ:
Ответ:
6) 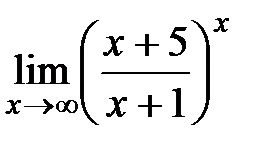 Ответ:
Ответ:
7).  Ответ:
Ответ:
8). 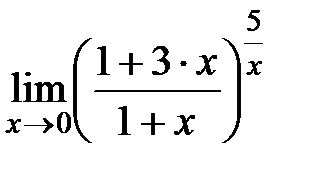 Ответ:
Ответ:
9).  Ответ:
Ответ:
10).  Ответ:
Ответ:
11). 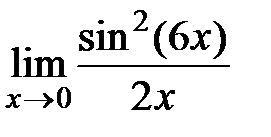 Ответ:
Ответ:
12). 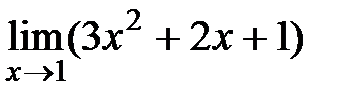 Ответ:
Ответ:
13).  Ответ:
Ответ:
2. Пользуясь определением производной, найти производную функции у, если:
1.  ,
,
2. 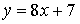 ,
,
3. у = 5 − 6x,
4. у = 4 − 7x,
5.  ,
,
6. 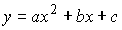 ,
,
7. у = 2х2 - 13х +3,
8. у=-3 x 2 -13 x,
9. у=7 x 2 +3 x,
10. у =4 – 5х + 2 х2,
11. у = 3х2 - 2х – 8,
12. у=х3- 9х – 4,
13. у=3х3 - 4х2 - 8х – 4,
14. у =-2х3 -4х2 -4х
|
|
|


