Тема: «Показательные уравнения и неравенства».

I. Определение: показательными уравнениями называют уравнения вида a^f(x) = a^g(x), где а – положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.

II. Теорема. Показательное уравнение a^f(x) = a^g(x) (где а > 0, а ¹ 1), равносильно уравнению f(x) = g(x).

III. Основные методы решения показательных уравнений:

1) функционально-графический;

2) метод уравнивания показателей;

3) метод введения новой переменной.

IV. Определение: показательными неравенствами называют неравенства вида a^f(x) > a^g(x), где а – положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.

V. Теорема. Показательное неравенство a^f(x) > a^g(x) равносильно неравенству того же смысла f(x) > g(x), если а > 1;

Показательное неравенство a^f(x) > a^g(x) равносильно неравенству противоположного смысла f(x) < g(x), если 0 < а < 1.

 

Урок-лекция

Тема: «Логарифм и его свойства. Логарифмическая функция».

I. Определение: логарифмом положительного числа b по положительному и отличному от 1 основанию а называют показатель степени, в которую нужно возвести число а, чтобы получить число b.

II. Формулы: log_aa = 1; log_a1 = 0; log_aa^c = c.

III. Свойства:

№ п/п	а > 1	0 < a < 1
1.	D(f) = (0; +¥)	D(f) = (0; +¥)
2.	Не является ни четной, ни нечетной
3.	Возрастает	Убывает
4.	Не ограничена сверху, не ограничена снизу
5.	Нет ни наибольшего, ни наименьшего значения
6.	Непрерывна	Непрерывна
7.	E(f) = (-¥; +¥)	E(f) = (-¥; +¥)
8.	Выпукла вверх	Выпукла вниз

IV. Теорема 1. Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел. log_abc = log_ab + log_ac.

Теорема 2. Если a, b, c – положительные числа, причем а ¹ 1, то справедливо равенство .

Теорема 3. Если a и b – положительные числа, причем а ¹ 1, то для любого числа r справедливо равенство log_ab^r = r log_ab.

Теорема 3. Равенство log_at = log_as, где a > 0, а ¹ 1, t > 0, s > 0, справедливо тогда и только тогда, когда t = s.

 

Урок-лекция

Тема: «Логарифмические уравнения и неравенства».

I. Определение: логарифмическими уравнениями называют уравнения вида log_af(x) = log_ag(x), где а – положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.

II. Теорема. Если f(x) > 0 и g(x) > 0, то логарифмическое уравнение log_af(x) = log_ag(x) (где а > 0, а ¹ 1) равносильно уравнению f(x) = g(x).

III. Основные методы решения логарифмических уравнений:

1) функционально-графический;

2) метод потенцирования;

3) метод введения новой переменной.

IV. Определение: логарифмическими неравенствами называют неравенства вида log_af(x) > log_ag(x), где а – положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.

V. Теорема. Если f(x) > 0 и g(x) > 0, то:

при а > 1 логарифмическое неравенство log_af(x) > log_ag(x) равносильно неравенству того же смысла f(x) > g(x);

при 0 < a 1 логарифмическое неравенство log_af(x) > log_ag(x) равносильно неравенству противоположного смысла f(x) < g(x).

VI. Теорема. Если a, b, c – положительные числа, причем а и с отличны от 1, то имеет место равенство .

Следствие 1. Если a и b – положительные и отличные от 1 числа, то справедливо равенство .

Следствие 2. Если a и b – положительные числа, причем а ¹ 1, то для любого числа r ¹ 1 справедливо равенство .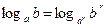

 

Урок-лекция

Тема: «Число е. Функция у = е^х».

I. Свойства функции у = е^х:

	D(f) = (-¥; +¥)
	не является ни четной, ни нечетной
	возрастает
	не ограничена сверху, ограничена снизу
	нет ни наибольшего, ни наименьшего значений
	непрерывна
	Е(f) = (0; +¥)
	выпукла вниз
	дифференцируема

II. Свойства функции у = ln(x):

	D(f) = (0; +¥)
	не является ни четной, ни нечетной
	возрастает
	не ограничена ни сверху, ни снизу
	нет ни наибольшего, ни наименьшего значений
	непрерывна
	Е(f) = (-¥; +¥)
	выпукла вверх
	дифференцируема

 

Список ключевых задач

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: