 |
Блок материла №2. Логарифмы. Логарифмическая функция.
|
|
|
|
Тест №7.5
Вариант 1.
- Найти область определения функции: y=log2(3x-2):
А) (-¥; +¥); Б) (0; +¥); В) (-¥; 2/3); Г) (2/3; +¥).
- Решить уравнение: log3(3x-5)=log3(x-3):
А) 4; Б) Æ; В) –2; Г) 1.
- Решить неравенство: log1/3(3-2x)³log1/3(1-x):
А) (2; +¥); Б) (1; 2); В) [2; +¥); Г) Æ.
Вариант 2.
1. Найти область определения функции: y=log3(2-5x):
А) (-¥; +¥); Б) (0; +¥); В) (-¥; 2/5); Г) (2/5; +¥).
2. Решить уравнение: log7(2x-3)=log7(x-2):
А) 1/3; Б) Æ; В) –5/3; Г) 1.
3. Решить неравенство: log1/2(2-3x)³log1/2(1-2x):
А) (1; +¥); Б) (0,5; 1); В) [1; +¥); Г) Æ.
Вариант 3.
1. Найти область определения функции: y=log3(2x-7):
А) (-¥; +¥); Б) (0; +¥); В) (-¥; 7/2); Г) (7/2; +¥).
2. Решить уравнение: log2(2x-7)=log2(3x-1):
А) -6; Б) Æ; В) 8/5; Г) -4.
- Решить неравенство: log1/5(5-2x)³log1/5(2-x):
А) (3; +¥); Б) (2; 3); В) [3; +¥); Г) Æ.
Вариант 4.
1. Найти область определения функции: y=log2(3-4x):
А) (-¥; +¥); Б) (0; +¥); В) (-¥; 3/4); Г) (3/4; +¥).
2. Решить уравнение: log5(5x-1)=log5(2x-3):
А) 3; Б) Æ; В) –2/3; Г) -1.
3. Решить неравенство: log1/4(7-2x)³log1/4(3-x):
А) (5; +¥); Б) (3,5; 5); В) [5; +¥); Г) Æ.
Тест самоконтроля:
- Определить log572, если известно, что log52=a, log53=b;
- Вычислить (log715+log74-log76)lg7.
Тест №7.6
Вариант 1.
- Решить уравнение log32x-log3x=2:
А) 1/9; Б) 3; В) {3; 1/9}; Г) {3; 1/9}.
2. Выбрать наибольшее число:
А) log1/38; Б) log35; В) log1/39.
3. Решить неравенство ln(2x-3)£ln(x+1):
А) (-¥; 4); Б) (1,5; 4); В) (-¥; 4]; Г) (1,5; +¥).
Вариант 2.
- Решить уравнение log0,52x-log0,5x=6:
А) 1/4; Б) 8; В) {8; 1/4}; Г) {8; 1/4}.
2. Выбрать наименьшее число:
А) log1/35; Б) log33; В) log1/39.
3. Решить неравенство ln(x+3)³ln(3x-1):
А) (-¥; 4); Б) (1,5; 4); В) (-¥; 4]; Г) (1,5; +¥).
Вариант 3.
- Решить уравнение log22x-log2x=2:
А) 1/4; Б) 2; В) {2; 1/4}; Г) {4; 1/2}.
2. Выбрать наибольшее число:
А) log37; Б) log43; В) log1/28.
3. Решить неравенство ln(5x-1)£ln(2x+3):
А) (-¥; 2); Б) (1/5; 2,5); В) (-¥; 2]; Г) (0,2;2].
Вариант 4.
|
|
|
- Решить уравнение log1/32x-log1/3x=6:
А) 1/9; Б) 27; В) {27; 1/9}; Г) {9; 1/27}.
2. Выбрать наименьшее число:
А) log37; Б) log1/28; В) log1/23.
3. Решить неравенство ln(4x-1)£ln(3x+7):
А) (-¥; 8); Б) (4;8]; В) (-¥; 8]; Г) (0,25;8].
Тест самоконтроля:
- Найти область значений функции y=log0.2(2x-7), если xÎ[-2; 0].
- Решить неравенство log0.5(2x-5)>-2.
Тест №7.7
Вариант 1.
1. Найти наибольшее значение функции y=log0.2(2x-3), если xÎ[1.52; 4]:
А) -1; Б) 2; В) 25; Г) 12.
2. Решить систему уравнений ì x+y=8
í
î log12x=1-log12y
А) (2; 6),(6; 2); Б) (2; 4), (4, 2); В) (5; 1), (1; 5); Г) (1; 7), (7; 1).
Вариант 2.
1. Найти наименьшее значение функции y=log0.25(3x-2), если xÎ[1; 2]:
А) 4; Б) 2; В) -1; Г) -8.
2. Решить систему уравнений ì x+y=6
í
î log2y=3-log2x
А) (1; 7),(7; 1); Б) (2; 4), (4, 2); В) (5; 1), (1; 5); Г) (2; 6), (6; 2).
Вариант 3.
1. Найти наименьшее значение функции y=log0.04(5x-4), если xÎ[1; 1,8]:
А) 5; Б) 12; В) -0,5; Г) -8.
2. Решить систему уравнений ì x+y=8
í
î log7y=1-log7x
А) (5; 1),(1; 5); Б) (1; 7), (7, 1); В) (2; 4), (4; 2); Г) (2; 6), (6; 2).
Вариант 4.
1. Найти наибольшее значение функции y=log0.5(3x-2), если xÎ[1; 10/3]:
А) 0; Б) 8; В) 4; Г) 2.
2. Решить систему уравнений ì x+y=6
í
î log5x=1-log5y
А) (2; 4),(4; 2); Б) (1; 7), (7, 1); В) (2; 6), (6; 2); Г) (5; 1), (1; 5).
Тест самоконтроля:
1. Решить уравнение log1/2(3x-5)=-2
2. Решить неравенство lg(2x-1)£lg(3x+4).
Тест№7.8
Вариант 1.
1. Найти область определения функции y=(log3(x2-9)):(1-x)1/2:
А) (-¥; -3); Б) (-3; 3); В) (1; 3); Г) x¹1.
2. Вычислить log275, если lg5=0.699; lg3=0.477:
А) 0,38; Б) 2,66; В) 2,11; Г) 0,47.
3. Какое из уравнений не имеет корней:
А) log3x=-2; Б) 1-x=log23; В) log3(-Öx)=0; Г) x-1=log23.
4. Решить неравенство (log2(3-x))/x³0:
А) [0; 2]; Б) x¹0; В) (-¥; 3); Г) (0; 2].
5. Решить уравнение log6(x+3)=1-log6(x+2):
А) {0; -5}; Б) {6}; В) {0}; Г) {0; 5}.
6. Решить систему уравнений ì 2log4x-log4(2y-1)=0.5
í
î x+2y=15
А) (4; 4,5); Б) (4; 4,5), (-7; 10); В) (-7;10); Г) (6; 3,5).
7. Найти множество точек пересечения графика функции y=log12(x+3)+log12(x+4)-1 с
осью абсцисс:
А) {-7; 0}; Б) {-3; -4}; В) {2; 5}; Г) {0}.
Вариант 2.
1. Найти область определения функции y=(log2(4-x2)):(x-1)1/2:
А) (2; +¥); Б) (-2; 2); В) (1; 2); Г) Æ.
|
|
|
2. Вычислить log330, если lg5=0.699; lg3=0.477:
А) 2,66; Б) 0,38; В) 2,11; Г) 0,47.
3. Какое из уравнений не имеет корней:
А) x=log30.7; Б) log3x=-2; В) 1-x=log23; Г) Öx=log20.7.
4. Решить неравенство (log2(3-x))/x£0:
А) [-2; 0]; Б) x¹0; В) (-¥; 3); Г) (-2; 0].
5. Решить уравнение log5(x+1)=1-log5(x+5):
А) {-6; 0}; Б) {6}; В) {6; 0}; Г) {0}.
6. Решить систему уравнений ì log9(2x-1)-2log9y=-0.5
í
î 2x-y=19
А) (9; 14), (6,5; -6); Б) (14; 9); В) (14; 9); Г) (6; 3,5).
7. Найти множество точек пересечения графика функции y=log14(x+2)+log14(x+7)-1 с
осью абсцисс:
А) {0}; Б) {-9; 0}; В) {0; 9}; Г) {9}.
Вариант 3.
1. Найти область определения функции y=(log5(x2-16)):(3-x)1/2:
А) (3; +¥); Б) (-5; 5); В) (3; 5); Г) x¹3.
2. Вычислить log524, если lg5=0.699; lg3=0.477:
А) 0.51; Б) 2.54; В) 0.39; Г) 1.97.
3. Какое из уравнений не имеет корней:
А) 1/x=log21; Б) log3x=-2; В) log0.5(1-x)=2; Г) log5x=log21.
4. Решить неравенство (log11(x-2))/(x-6)£0:
А) [3; 6]; Б) x¹6; В) (3; +¥); Г) [2; 6].
5. Решить уравнение log14(x+2)+log14(x+7)=1:
А) {0}; Б) {-9; 0}; В) {9}; Г) {0; 9}.
6. Решить систему уравнений ì 2log4y-log4(2x-1)=0.5
í
î y+2x=13
А) (4.5; 4), (10; 7); Б) (4.5; 4); В) (6; 5.5); Г) (4; 4,5).
7. Найти множество точек пересечения графика функции y=log6(x+3)+log6(x+2)-1 с
осью абсцисс:
А) {0; 5}; Б) {0}; В) {0; -5}; Г) {6}.
Вариант 4.
1. Найти область определения функции y=(log2(x2-25)):(x-3)1/2:
А) (5; +¥); Б) (-5; 5); В) (1; 5); Г) x¹3.
2. Вычислить log260, если lg5=0.699; lg3=0.477:
А) 0.51; Б) 2.54; В) 0.39; Г) 1.97.
3. Какое из уравнений не имеет корней:
А) log2x=-2; Б) x=log21; В) log0.5(1-x)=2; Г) x-1=log25.
4. Решить неравенство (log3(8-x))/(4-x)£0:
А) [4; 7]; Б) x¹4; В) (4; 7]; Г) [4; 7).
5. Решить уравнение log12(x+3)+log12(x+4)=1:
А) {-6; 0}; Б) {6}; В) {6; 0}; Г) {-6}.
6. Решить систему уравнений ì 2log9x-log9(2y-1)=0.5
í
î 2y-x=19
А) (14; 9); Б) (6.5; 6), (9; 14); В) (-6; 6.5); Г) (9; 14).
7. Найти множество точек пересечения графика функции y=log5(x+1)+log5(x+5)-1 с
осью абсцисс:
А) {-9; 0}; Б) {0; 9}; В) {0}; Г) {9}.
Тест №7.9
Вариант 1.
Уровень А.
А1. Упростить выражение log515+log575-2log53:
А) 3; Б) 32; В) 51; Г) 4.
А2. Найдите область определения функции y=log3(x-2):
А) (-¥; 2); Б) (-¥; 2]; В) (2; +¥); Г) [2; +¥).
А3. Укажите промежуток, которому принадлежит корень уравнения log2(x+1)=4:
А) (8; 10); Б) (14; 16); В) (6; 8); Г) (4; 6).
А4. Решите неравенство log0.4(1.9x-1.3)³-1:
А) (13/19; 2]; Б) (-¥; 2]; В) [2; +¥); Г) (12/19; 13/19].
Уровень В.
В1. Найти сумму корней уравнения log1/54x+log5(x2+75)=1 (ответ: xÎ{5; 15})
B2. Найти число целых решений неравенства log22x-log2x£6 (ответ: 7)
В3. Найти отношение x0/y0, где x0 и y0 – решения системы уравнений ì log3x+log9y=3
|
|
|
í
î log1/3x+log3y=3
(ответ: 1/27)
Уровень С.
С1. Решить уравнение lgx2+lg(x+10)2=2lg11 (ответ: x=1)
С2. Решить неравенство (x-1)log1/3x+ 1/2logx1/3³0 (ответ: xÎ(0; 0.5] È (1; +¥))
Вариант 2.
Уровень А.
А1. Упростить выражение (log798-log714)/7:
А) 8; Б) 1/7; В) -1; Г) -1/4.
А2. Найдите область определения функции y=log3(x+4):
А) (-¥; -4); Б) (-¥; -4]; В) (-4; +¥); Г) [-4; +¥).
А3. Укажите промежуток, которому принадлежит корень уравнения lg5x=2:
А) (8; 10); Б) (14; 16); В) (19; 21); Г) (94; 96).
А4. Решите неравенство log2(1-0.3x)³4:
А) (10/3; 50); Б) (-¥; -50]; В) [-50; +¥); Г) (-¥; 10/3].
Уровень В.
В1. Найти наибольший корень уравнения log22x-3log2x-4=0 (ответ: x=0,5)
B2. Найти число целых решений неравенства log2(x-1)-log1/2x£1 (ответ: 3)
В3. Найти разность x0-y0, где x0 и y0 – решения системы уравнений ì log3(x-y)=1
í
î log4x-log4y=2
(ответ: 3)
Уровень С.
С1. Решить уравнение ç2+x/9çlog3ç(18+x)/9ç=81 (ответ: xÎ{-99; -19; -17; 63})
С2. Решить неравенство log2x5>log3x+15 (ответ: xÎ(0; 0.5) È (0.5; +¥))
Вариант 3.
Уровень А.
А1. Упростить выражение log23+log224-log29:
А) 3; Б) 8; В) log218; Г) 4.
А2. Найдите область определения функции y=log5(2-x):
А) (-¥; 2); Б) (-¥; 2]; В) (2; +¥); Г) [2; +¥).
А3. Укажите промежуток, которому принадлежит корень уравнения log3(1-x)=4:
А) (62; 64); Б) (-81; -79); В) (79; 81); Г) (-12; -10).
А4. Решите неравенство log2(3-5x)<2:
А) (-0.2; 0.6); Б) (3/5; 2); В) (2; +¥); Г) (0.6; +¥).
Уровень В.
В1. Найти решение уравнения logÖ2(x+1)+2log2(x+1)=4 (ответ: xÎ{1})
B2. Найти наименьшее целое решение неравенства lg2x+6<5lgx (ответ: 101)
В3. Найти отношение x0/y0, где x0 и y0 – решения системы уравнений ì log3x-log3y=2
í
î x(y-2)=27
(ответ: 9)
Уровень С.
С1. Решить уравнение 3log3x=2log9xx2 (ответ: xÎ{3-2/3; 1})
С2. Решить неравенство log2(x-3)2+log2(x-3)³1 (ответ: xÎ[3+21/3; +¥))
Вариант 4.
Уровень А.
А1. Упростить выражение 21+log26:
А) 12; Б) 8; В) 24; Г) 7.
А2. Найдите область определения функции y=log2/3(4-x):
А) (-¥; 4); Б) (-¥; 4]; В) (4; +¥); Г) [4; +¥).
А3. Укажите промежуток, которому принадлежит корень уравнения lg(x-10)=1:
А) (19; 21); Б) (-1; 1); В) (-11; -9); Г) (9; 11).
А4. Решите неравенство log2(3x-1)<1:
А) (1/3; 1); Б) (-¥; 1); В) (1/3; +¥); Г) (-1;1/3).
Уровень В.
В1. Найти наибольший корень уравнения log42x+log4Öx=1,5 (ответ: xÎ{161/3})
|
|
|
B2. Найти число целых решений неравенства log1/7(2x+3)<-log7(3x-2) (ответ: 4)
В3. Найти отношение x0*y0, где x0 и y0 – решения системы уравнений
ì 3log0.5x+2y+1=5
í
î 2y+log2x=5
(ответ: 4)
Уровень С.
С1. Решить уравнение log10/7(lg(x+1)-1)-1=log0.7(3lg(x+1)-1)-log0.7(lg(x+1)+3)
(ответ: xÎ{0.9; 99})
С2. Решить неравенство log2(x+2)4>4log2(x-3)+8 (ответ: xÎ(3; 14/3))
Система задач
Задачи берутся из учебника Мордковича, а также можно использовать следующие упражнения:
- Постройте график функции:
а) y = 0,4x + 1; б) y = log2(x - 2); в) y = 2x – 3; г) 
- Вычислите:
а)  б)
б) 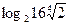 в)
в)  г)
г) 
- Найдите точки экстремума функции:
а)  б)
б)  в)
в)  г)
г) 
- Составьте уравнение той касательной к графику функции: а)
 ; б)
; б)  , которая проходит через начало координат.
, которая проходит через начало координат. - Решите показательное уравнение:
а)  б)
б)  в)
в) 
г)  д)
д)  е)
е) 
ж)  з)
з) 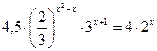 и)
и) 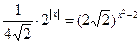
к)  л)
л) 
м)  н)
н) 
о) 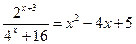 п)
п)  р)
р) 
- Решите логарифмическое уравнение:
а)  б)
б) 
в)  г)
г) 
д) 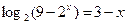 е)
е)  ж)
ж) 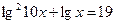
з) 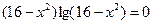 и)
и)  к)
к) 
л)  м)
м) 
- Найдите все значения параметра а, при котором уравнение (х-а)log2x = 0 имеет единственное решение?
- Выберите наибольшее решение уравнения:
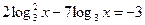 .
. - Решите неравенства и системы:
а)  б)
б)  в)
в) 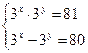 г)
г) 
д)  е)
е)  ж)
ж) 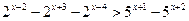
з)  и)
и)  к)
к)  л)
л) 
м) 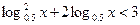 н)
н)  о)
о) 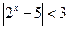 п)
п) 
р) 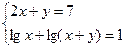 с)
с)  т)
т) 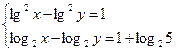
- Решите неравенство
 . Верно ли, что число
. Верно ли, что число  является решением неравенства?
является решением неравенства?
Тесты
| Показательная функция. Уровень А. | |||||||||||||
Тест I. Вариант 1.
1. Вычислить 
| Тест I. Вариант 2.
1. Вычислить 
| ||||||||||||
а) 
| б) 
| в) 5 | г) 25 | а) 3 | б) 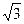
| в) 9 | г) 
| ||||||
2. Определить х, если 
| 2. Определить х, если 
| ||||||||||||
| а) 3 | б) 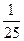
| в) -3 | г) 
| а) 3 | б) 16 | в) 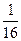
| г) -3 | ||||||
| 3. Сравнить числа и выбрать из них наибольшее: | 3. Сравнить числа и выбрать из них наименьшее: | ||||||||||||
а) 
| б) 
| в) 1 | г) 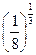
| а) 
| б) 
| в) 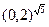
| г) 1 | ||||||
4. Найти область определения функции: 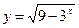
| 4. Найти область определения функции: 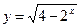
| ||||||||||||
| а) (-¥; -2) | б) (2; +¥) | в) [2; +¥) | г) (-¥; 2] | а) (-¥; 2] | б) (-¥; 2) | в) (2; +¥) | г) [2; +¥) | ||||||
| Тест II. Вариант 1. 1. Найти область значения функции у = 2х + 1 | Тест II. Вариант 2.
1. Найти область значения функции 
| ||||||||||||
| а) (-8; 1) | б) [1; +¥) | в) (1; +¥) | г) (-1; +¥) | а) (-¥; 1) | б) (-¥; 1] | в) [-1; +¥) | г) (-1; +¥) | ||||||
| 2. Найти множество точек пересечения с осью абсцисс графика функции у = 52х – 7х – 17 × 52х + 17 × 7х | 2. Найти множество точек пересечения с осью абсцисс графика функции у = 22х - 1 – 32х – 32х - + 2х + 2 | ||||||||||||
| а) {1} | б) {5/7} | в) {0,1; 1} | г) {0} | а) {1,5} | б) {3} | в) {0,5} | г) {0,5; 2} | ||||||
| 3. Какая из функций является возрастающей? | 5. Какая из функций является убывающей? | ||||||||||||
а) 
| б) 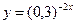
| в) 
| г) 
| а) 
| б) 
| в) 
| г) 
| ||||||
4. Найти область определения функции 
| 4. Найти область определения функции 
| ||||||||||||
| а) (-¥; 3] | б) [3; +¥) | в) (-¥; -3] | г) [-3; +¥) | а) [-1; +¥) | б) (-¥; -1] | в) (-¥; 1] | г) [1; +¥) | ||||||
| Уровень Б. | |||||||||||||
Тест I. Вариант 1.
1. Решить уравнение: 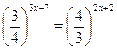
| Тест I. Вариант 2.
1. Решить уравнение: 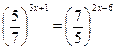
| ||||||||||||
| а) -1 | б) 1 | в) 7 | г) -7 | а) 2 | б) -2 | в) 1 | г) -1 | ||||||
2. Решить уравнение: 
| 2. Решить уравнение: 
| ||||||||||||
| а) 1 | б) 3 | в) 1/2 | г) -3 | а) –1,5 | б) -3 | в) 1 | г) -1 | ||||||
| 3. Решите неравенство: 52х + 1 > 1 – 4 × 5х | 3. Решите неравенство: 11 × 3х > 4 – 3 × 9х | ||||||||||||
| а) (-¥; 1) | б) (-1; +¥) | в) (-1; 0) | г) (-¥; 1) | а) (-¥; 1) | б) (-1; 0) | в) (-1; +¥) | г) (-¥; 1) | ||||||
4. Решить систему: 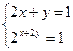
| 4. Решить систему: 
| ||||||||||||
| а) (-5/3; 4/3) | б) (-1; 2) | в) (4/3; -5/3) | г) (1; 3) | а) (-5/3; 4/3) | б) (-1; 2) | в) (0; 1) | г) (5/3; -4/3) | ||||||
| Тест II. Вариант 1. 1. Найти произведение корней уравнения: 4х + 64 = 20 × 2х | Тест II. Вариант 2. 1. Найти произведение корней уравнения: 9х + 27 = 28 × 3х | ||||||||||||
| а) 16 | б) 64 | в) 32 | г) 8 | а) 0 | б) 27 | в) 3 | г) 9 | ||||||
2. Решите неравенство: 
| 2. Решите неравенство: 
| ||||||||||||
| а) (-¥; 2) | б) (-2; +¥) | в) (-2; 0) | г) (0; +¥) | а) (-¥; 0) | б) (-1; +¥) | в) (-1; 0) | г) (0; +¥) | ||||||
3. Определить наименьшее значение функции 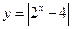 на отрезке [-2; 4]. на отрезке [-2; 4].
| 3. Определить наибольшее значение функции 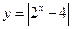 на отрезке [-2; 4]. на отрезке [-2; 4].
| ||||||||||||
| а) 3,75 | б) 0 | в) 3 | г) 12 | а) 12 | б) 3,75 | в) 3 | г) 0 | ||||||
4. Найти абсциссу точки пересечения графиков функции  , ,  . .
| 4. Найти абсциссу точки пересечения графиков функции  , ,  . .
| ||||||||||||
| а) 2 | б) -2 | в) 1 | г) -1 | а) -1 | б) 1 | в) 7 | г) -7 | ||||||
| Уровень В. | |||||||||||||
Тест I. Вариант 1.
1. Вычислите: 
| Тест I. Вариант 2.
1. Вычислите: 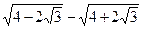
| ||||||||||||
| а) 2 | б) 1 | в) 
| г) - 
| а) 2 | б) -2 | в) 
| г) - 
| ||||||
| 2. Выбрать наибольшее из чисел, если известно, что х>y>0: | 2. Выбрать наименьшее из чисел, если известно, что х>y>0 | ||||||||||||
| а) 3у | б) 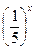
| в) 2у | г) 1 | а) 2у | б) 
| в) 1 | г) 3х | ||||||
3. Найти сумму корней уравнения: 
| 3. Найти сумму корней уравнения: 
| ||||||||||||
| а) 1 | б) 2 | в) 0 | г) 4 | а) 1 | б) 4 | в) 2 | г) 0 | ||||||
4. Решить неравенство: 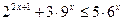
| 4. Решить неравенство: 
| ||||||||||||
| а) [0; 1] | б) (-¥; 1] | в) [-1; 0] | г) [-1; +¥) | а) [-1; +¥] | б) [0; 1] | в) [1; +¥) | г) [-1; 0] | ||||||
Тест II. Вариант 1.
1. Найти значение выражения: 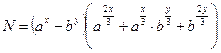 при х = 2, у = 1, а = 27, b = 8 при х = 2, у = 1, а = 27, b = 8
| Тест II. Вариант 2.
1. Найти значение выражения:  при х = 1, у = 2, а = 8, b = 27 при х = 1, у = 2, а = 8, b = 27
| ||||||||||||
| а) 7 | б) 11 | в) 13 | г) 21 | а) 7 | б) 11 | в) 13 | г) 21 | ||||||
2. Найти значения х, при которых у1(х) > у2(х), если  , ,  . .
| 2. Найти значения х, при которых у1(х) < у2(х), если  , ,  . .
| ||||||||||||
| а) (-¥; 1) | б) (-1; 0) | в) (0,6; 1) | г) (0; 1) | а) (-¥; -1) | б) (-1; 0) | в) (0; 1) | г) (5/6; 1) | ||||||
3. Найти сумму корней ур-ия: 
| 3. Найти сумму корней ур-ия: 
| ||||||||||||
| а) 0 | б) 4 | в) 2 | г) -4 | а) 4 | б) 0 | в) 2 | г) -2 | ||||||
| 4. При радиоактивном распаде масса вещества за сутки уменьшается в 2 раза. На сколько уменьшится 24г вещества за 6 суток? | 4. При размножении микробов масса вещества за 1,5ч увеличивается в 2 раза. На сколько увеличится 0,5г вещества за 6 ч? | ||||||||||||
| а) 3г | б) 21г | в) 23,5г | г) 5г | а) 8г | б) 6г | в) 7,5г | г) 12г | ||||||
| Логарифмическая функция. Уровень А. | |||||||||||||
| Тест I. Вариант 1. 1. Определить log572, если log52 = a, log53 = b | Тест I. Вариант 2. 1. Определить log560, если log52 = a, log53 = b | ||||||||||||
| а) 3a + b | б) 2a + 3b | в) a - b | г) a + b | а) 2a + b | б) 1 + a + b | в) 3a + b | г) 1 + 2a + b | ||||||
2. Вычислить: 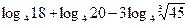
| 2. Вычислить: 
| ||||||||||||
| а) 1,5 | б) 1 | в) -1,5 | г) -1 | а) 1/3 | б) –1/3 | в) 4/3 | г) 1 | ||||||
| 3. Найти область определения функции: у = log2(3x - 2) | 3. Найти область определения функции: у = log3(2 - 5x) | ||||||||||||
| а) (-¥; +¥) | б) (0; +¥) | в) (-¥; 2/3) | г) (2/3; +¥) | а) (-¥; 2/5) | б) (-¥; +¥) | в) (2/5; +¥) | г) (0; +¥) | ||||||
| 4. Сравнить числа и выбрать из них наибольшее: | 4. Сравнить числа и выбрать из них наименьшее: | ||||||||||||
| а) 1 | б) 
| в) log35 | г) 
| а) 
| б) 1 | в) log33 | г) 
| ||||||
Тест II. Вариант 1.
1. Вычислить: 
| Тест II. Вариант 2.
1. Вычислить: 
| ||||||||||||
| а) 3/4 | б) 1/4 | в) –1/4 | г) 4/3 | а) 1 | б) 0 | в) –1 | г) 1/2 | ||||||
| 2. Найти наибольшее значение функции: у = log0,2(2x - 3), если хÎ[1,52; 4]. | 2. Найти наименьшее значение функции: у = log0,25(3x - 2), если хÎ[1; 2]. | ||||||||||||
| а) -1 | б) 2 | в) 25 | г) 12 | а) 2 | б) 4 | в) -1 | г) -8 | ||||||
3. Найти область определения функции: 
| 3. Найти область определения функции: 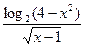
| ||||||||||||
| а) (-¥; -3) | б) (-3; 3) | в) х ¹ 1 | г) (1; 3) | а) (-2; 2) | б) (1; 2) | в) (2; +¥) | г) х ¹ 1 | ||||||
| 4. Определить log572, если известно, что lg5 = 0,699, lg3 = 0,477. | 4. Определить log530, если известно, что lg5 = 0,699, lg3 = 0,477. | ||||||||||||
| а) 0,38 | б) 2,66 | в) 2,11 | г) 0,47 | а) 2,66 | б) 0,38 | в) 2,11 | г) 0,47 | ||||||
| Уровень Б. | |||||||||||||
Тест I. Вариант 1.
1. Решить уравнение: 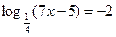
| Тест I. Вариант 2.
1. Решить уравнение: 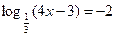
| ||||||||||||
| а) 1 | б) 2 | в) 3 | г) 4 | а) 2 | б) 4 | в) 1 | г) 3 | ||||||
2. Решить систему: 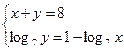
| 2. Решить систему: 
| ||||||||||||
| а) (5;1); (1;5) | б) (2;4); (4;2) | в) (1;7); (7;1) | г) (2;6); (6;2) | а) (2;4); (4;2) | б) (2;6); (6;2) | в) (1;7); (7;1) | г) (5;1); (1;5) | ||||||
| 3. Решить неравенство: log5(3x + 1) ³ log5(2x - 1) | 3. Решить неравенство: log4(2x - 3) £ log4(4x + 7) | ||||||||||||
| а) (0,5; +¥) | б) [0,5; +¥) | в) [-2; +¥) | г) (-¥; 0,5) | а) [-5; +¥) | б) (1,5; +¥) | в) (-¥; 1,5) | г) [1,5; +¥) | ||||||
| 4. Какое из уравнений не имеет корней: | 4. Какое из уравнений не имеет корней: | ||||||||||||
| а) log3x = -2 | б) 1-x = log23 | в) log3(-  ) )
| г) x-1 = log23 | а) x = log30,7 | б) log3x = -2 | в) 1-x=log23 | г)  =log30,7 =log30,7
| ||||||
| Тест II. Вариант 1. 1. Решить уравнение: log2(2x - 7) = log2(3x - 1) | Тест II. Вариант 2. 1. Решить уравнение: log5(5x - 1) = log5(2x - 3) | ||||||||||||
| а) -6 | б) 8/5 | в) -4 | г) Æ | а) Æ | б) -2/3 | в) -1 | г) 3 | ||||||
2. Решить неравенство: 
| 2. Решить неравенство: 
| ||||||||||||
| а) [0; 2] | б) х ¹ 0 | в) (-¥; 3) | г) (0; 2] | а) [-2; 0) | б) [-2; 0] | в) (-¥; 3) | г) x = 0 | ||||||
| 3. Решить уравнение: log6(x + 3) = 1 – log6(x + 2) | 3. Решить уравнение: log5(x + 1) = 1 – log5(x + 5) | ||||||||||||
| а) {0; -5} | б) {6} | в) {0} | г) {0; 5} | а) {-6; 0} | б) {6} | в) {6; 0} | г) {0} | ||||||
4. Решить систему: 
| 4. Решить систему: 
| ||||||||||||
| а) (4; 4,5) | б) (-7; 10) | в) (4; 4,5); (-7; 10) | г) (6; 3,5) | а) (9; 14) | б) (14; 9) | в) (6,5; -6); (14; 9) | г) (6; 3,5) | ||||||
| Уровень В. | |||||||||||||
Тест I. Вариант 1.
1. Решить неравенство: 
| Тест I. Вариант 2.
1. Решить неравенство: 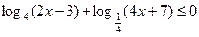
| ||||||||||||
| а) (0,5; +¥) | б) [0,5; +¥) | в) [-2; +¥) | г) (-¥; 0,5) | а) [-5; +¥) | б) (1,5; +¥) | в) (-¥; 1,5) | г) [1,5; +¥) | ||||||
| 2. Решить уравнение: log2x – 1 = 2logx2 | 2. Решить уравнение: 
| ||||||||||||
| а) ¼; 2 | б) ½; 4 | в) 2 | г) 1/4 | а) 1/9; 27 | б) 27 | в) 1/27; 9 | г) 3; 1/9 | ||||||
3. Решить систему: 
| 3. Решить систему: 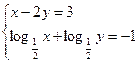
| ||||||||||||
| а) (-1; -4) | б) (-1; -4); (16; 1/4) | в) (16; 1/4) | г) (1/2; 8) | а) (-1; -2); (1/2; 4) | б) (-1; -2) | в) (1/2; 8) | г) (4; 1/2) | ||||||
4. Решить систему: 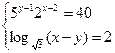
|  4. Решить систему: 4. Решить систему: 
| ||||||||||||
| а) (0; 3) | б) (3; 1) | в) (5; 2) | г) (4; -2) | а) (0; 3) | б) (3; 1) | в) (5; 2) | г) (4; -2) | ||||||
| Тест II. Вариант 1. 1. Вычислить: log214 – log25 log53 log37 | Тест II. Вариант 2. 1. Вычислить: log424 – log49 log913 log136 | ||||||||||||
| а) 3 | б) 4 | в) 1 | г) 2 | а) 4 | б) 1 | в) 2 | г) 3 | ||||||
| 2. Какому из промежутков принадлежит область определения функции: y = logctgx sinx | 2. Какому из промежутков принадлежит область определения функции: y = logtgx cosx | ||||||||||||
| а) (0; p/4) | б) (p/2; p) | в) (-p/4; 0) | г) (3p/4; p) | а) (p/2; p) | б) (0; p/4) | в) (-p/4; 0) | г) (3p/4; p) | ||||||
3. Какой из промежутков не принадлежит решению неравенства: 
| 3. Какой из промежутков принадлежит решению неравенства: 
| ||||||||||||
| а) (1; 1,5) | б) (1,5; 2) | в) (0; 0,5) | г) (0,5; 1) | а) (1; 1,5) | б) (1; 2) | в) (1,5; 2) | г) (0; 0,5) | ||||||
4. Найти сумму решений уравнения: 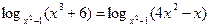
| 4. Найти сумму решений уравнения: 
| ||||||||||||
| а) 4 | б) 5 | в) 1 | г) 6 | а) 5 | б) 4 | в) 3 | г) 2 | ||||||
|
|
|
|
|
|


