Урок решения ключевых задач

1. Решить уравнения и неравенства графически а) 2^х = 4; б) 2^х > 1.

а) строим в одной системе координат графики функций у = 2^х и у = 4.

Ответ: х = 2.

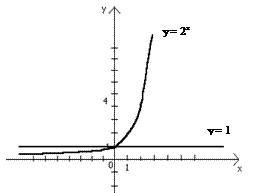б) рисунок этот же, но прямая не у = 4, а у = 1.

Ответ: х Î (0; +¥)

№ 1320(в).

1. Решить уравнение:

а) 2^2х-4 = 64 64 = 2⁶

2^2х-4 = 2⁶

2х-4 = 6

2х = 10

х = 5

Ответ: х = 5

б)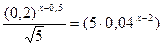

Упростим числитель, знаменатель левой части и правую часть:

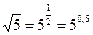
-х = 5-2х

х = 5

Ответ: х = 5

в) 4^х + 2^х+1 – 24 = 0

(2^х)² + 2×2^х – 24 = 0

Введем новую переменную: у = 2^х

у² + 2у – 24 = 0

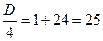
у₁ = -1 + 5 = 4 у₂ = -1 - 5 = -6

1) 2^х = 4 2) 2^х = -6

2^х = 2² не имеет решения

х = 2

Ответ: х = 2

№ 1361(г); 1368(г)

1. Решить неравенство:

Введем новую переменную: t = 2^х

Решаем получившееся неравенство методом интервалов:

 

< t < 9

< 3^х < 9

3^-1< 3^х < 3²

-1 < х < 2

Ответ: х Î (-1; 2)

№ 1411(а)

 

Урок решения ключевых задач

1. у = log2(x + 2) - 3

   
   Построить график функции у = log₂(x + 2) – 3.

 

График функции у = log₂(x + 2) – 3 получается из графика функции у = log₂(x) параллельным переносом вдоль оси абсцисс на 2 единицы влево и параллельным переносом вдоль оси ординат на 3 единицы вниз.

№ 1475(а)

1. Решить уравнение:

а) log₃(x² – 3x - 5) = log₃(7 – 2x)

x² – 3x - 5 = 7 – 2x

x² – x - 12 = 0

D = 1 + 48 = 49

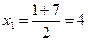
Проверка:

1) х = 4

4² – 3 × 4 – 5 = -1 -1 < 0

х₁ = 4 – посторонний корень

2) х = -3

(-3)² – 3 × (-3) – 5 =13 13 > 0

7 – 2 × (-3) = 13 13 > 0

Ответ: х = 3

б) log₂(x + 4) + log₂(2x + 3) = log₂(1 – 2x)

log₂(x + 4)(2x + 3) = log₂(1 – 2x)

(x + 4)(2x + 3) = 1 – 2x

2х² + 8х + 3х + 12 = 1 – 2х

2х² + 13х + 11 = 0

D = 169 + 88 = 81

Проверка:

1) х = -1

-1 + 4 = 3 3 > 0

2 × (-1) + 3 = 1 1 > 0

1 – 2 × (-1) = 3 3 > 0

2) х =

< 0

х = - посторонний корень

Ответ: х = -1

в)

Упростим:

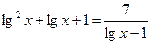
Введем новую переменную: у = lg x

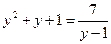
(у-1)(у² + у + 1) = 7

у³ – 1 = 7

у³ = 8

у = 2

lg x = 2

х = 100

Ответ: х = 100

№ 1554(а); 1552(б); 1557(а)

1. Решить неравенство:

Упростим:

Так как < 1, то

16 + 4х – х² ³ 16

-

+

+

х² – 4х £ 0

х (х - 4) £ 0

 

0 £ х £ 4

Ответ: х Î [0; 4]

№ 1579(а); 1584(а)

 

Номерные тесты

Блок материала №1. Показательная функция.

Тест №7.1

Вариант 1.

1. Вычислить: (2^(Ö3+1)²*4^-Ö3)^1/2:

А) 8; Б) 4; В)2^Ö3; Г) Ö2.

1. Решить уравнение: 9^x-4*3^x+1=13:

А) {1; 3}; Б) {1; 2}; В) {1; 4}; Г) {0; 1}.

1. Решить неравенство: 1³2^2x-9:

А) [0; +¥); Б) (-¥; -4,5]; В) (-¥; -4,5); Г) [4,5; +¥).

 

Вариант 2.

1. Вычислить: (3^(Ö3-1)²:9^-Ö3)^1/2:

А) 3; Б) 9; В)3^Ö3; Г) Ö3.

1. Решить уравнение: 25^x-6*5^x+1+5=0:

А) {1; 3}; Б) {0; 2}; В) {1; 5}; Г) {0; 1}.

1. Решить неравенство: 5^4x-7³1:

А) (1,75; +¥); Б) (-¥; -1,75]; В) (-¥; -1,75); Г) [1,75; +¥).

 

Вариант 3.

1. Вычислить: (5^(Ö5+1)²*25^-Ö5)^1/3:

А) 5; Б) 25; В)5^Ö5; Г) Ö5.

1. Решить уравнение: 4^x-5*2^x+4=0:

А) {1; 4}; Б) {0; 2}; В) {1; 2}; Г) {2; 4}.

1. Решить неравенство: 3^3x-6³1:

А) [2; +¥); Б) (-¥; -2]; В) (-¥; 2]; Г) [-2; +¥).

 

Вариант 4.

1. Вычислить: (3^(Ö3+1)²:9^Ö3)^1/4:

А) 3; Б) 9; В)3^Ö3; Г) Ö3.

1. Решить уравнение: 16^x-5*4^x+4=0:

А) {1; 4}; Б) {0; 4}; В) {1; 2}; Г) {0; 1}.

1. Решить неравенство: 1³7^5x-12:

А) [2,4; +¥); Б) (-¥; 2,4]; В) (-¥; 2,4); Г) (2,4; +¥).

 

Тест самоконтроля:

1. Решить уравнение: 2*5^x+5^x+1=35;

2. Решить неравенство: (1/3)^x-1+(1/3)^x+1³10.

 

Тест №7.2

Вариант 1.

1. Решить уравнение: 2^1/3(6x-3)=(8^2x-1)^1/4:

А) {0,5; 4}; Б) {4}; В) {-4; 0,5}; Г) {–0,5; 4}.

1. Решить неравенство: 2+2/49³(0,7)^x:

А) (-¥; -2]; Б) [-2; +¥); В) (-¥; 2]; Г)[2; +¥).

1. Решить неравенство: (ctg p/6)^x+1<0:

А) (-¥; 1); Б) (1; +¥); В) (-¥; -1); Г) (-1; -¥).

 

Вариант 2.

1. Решить уравнение: 4^1/x(6x+3)=(64^2x+1)^1/4:

А) {0,5; 4}; Б) {4}; В) {-4; 0,5}; Г) {–0,5; 4}.

1. Решить неравенство: (0,35)^x³2+6/7

А) (-¥; -1]; Б) [-1; +¥); В) (-¥; 1]; Г)[1; +¥).

1. Решить неравенство: (cos p/6)^x+0,5>Ö2:

А) (-¥; 1); Б) (1; +¥); В) (-¥; -1); Г) (-¥;1).

Вариант 3.

1. Решить уравнение: 5^1/x(6x+3)=(125^2x+1)^1/4:

А) {2}; Б) {4}; В) {-4; 0,5}; Г) {–0,5; 4}.

1. Решить неравенство: (0,3)^x³11+1/9

А) (-¥; -2]; Б) [2; +¥); В) (-¥; 2]; Г)[2; +¥).

1. Решить неравенство: (tg p/6)^x-1>9^-0,5:

А) (-¥; 1); Б) (1; +¥); В) (-¥; -1); Г) (-¥;1).

 

Вариант 4.

1. Решить уравнение: 3^1/x(6x-3)=(27^2x-1)^1/4:

А) {-0,5; -4}; Б) {0,5; 4}; В) {-4; 0,5}; Г) {–0,5; 4}.

1. Решить неравенство: (0,9)^x³1+19/81

А) (-¥; -2]; Б) [2; +¥); В) (-¥; 2]; Г)[-2; +¥).

1. Решить неравенство: (cos p/6)^x+0,5>Ö2:

А) (-¥; 1); Б) (1; +¥); В) (-¥; -1); Г) (-¥;1).

 

Тест самоконтроля:

1. Решить уравнение: (cos p/3)^2x-1=8;
2. Решить неравенство: 9^x>3^x+6.

 

Тест №7.3

Вариант 1.

1. Выбрать наибольшее число:

А) (1/3)^-2,25; Б) 1; В) 3^1,5; Г) (Ö3)^Ö3;

1. Найти наименьшее значение функции y=ê2^x-4êна отрезке [-2; 4]:

А) 3,75; Б) 0; В) 3; Г) 12.

1. Найти абсциссу точки пересечения графиков функций: y=(1,4)^2x-6 и y=(5/7)^3x+1:

А) 2; Б)-2; В)1; Г)-1.

1. Решить неравенство: 3^x+1*9^x-0,5³3^1/3:

А) [-1/9; +¥); Б) (-¥; -1/9]; В) (-¥; 1/9]; Г) [1/9; +¥).

1. Найти сумму корней уравнения: (0,25)^x+1*9^x-0,5=Ö8:

А)-1; Б) 3; В)2; Г)-2.

1. Найти значение выражения: z=(x^(y+1)²*25^-Öy)^1/3 при x=5; y=Ö5:

А) 5^Ö5; Б) Ö5; В) 5; Г)25.

 

Вариант 2.

1. Выбрать наибольшее число:

А) (1/2)^-1; Б) 1; В) (1/2)^-2,1; Г) (Ö2)^Ö2;

1. Найти наименьшее значение функции y=ê3^x-1êна отрезке [-2; 2]:

А) 8/9; Б) 0; В) 8; Г) 2.

1. Найти абсциссу точки пересечения графиков функций: y=(0,8)^3x-7 и y=(5/4)^2x+2:

А) 9; Б)-9; В)1; Г)-1.

1. Решить неравенство: 2^x+1*8^x-0,5³2^1/2:

А) [-1/4; +¥); Б) (-¥; -1/4]; В) (-¥; 1/4]; Г) [1/4; +¥).

1. Найти сумму корней уравнения: 5^x²*(0,2)^2x+5=(1/5)³:

А)2Ö3; Б) 3; В)2; Г)-2.

1. Найти значение выражения: z=(x^(y+1)²:9^y)^1/4 при x=3; y=Ö3:

А) 3^Ö3; Б) Ö3; В) 3 Г)9.

 

Вариант 3.

1. Выбрать наибольшее число:

А) (1/7)^-2,5; Б) 1; В) (1/7)^-2,7; Г) (Ö7)^-Ö5;

1. Найти наименьшее значение функции y=ê3^x-1êна отрезке [-2; 2]:

А) 8/9; Б) 0; В) 8; Г) 2.

1. Найти абсциссу точки пересечения графиков функций: y=(0,8)^3x-7 и y=(5/4)^2x+2:

А) 9; Б)-9; В)1; Г)-1.

1. Решить неравенство: Ö5³5^x-1*25^x-0,5:

А) [-5/6; +¥); Б) (-¥; 5/6]; В) (-¥; -5/6]; Г) [5/6; +¥).

1. Найти сумму корней уравнения: 2^x²+6,5*(0,5)^5x=Ö2:

А)5; Б) 3; В)2; Г)-5.

1. Найти значение выражения: z=(x^(y+1)²:4^-y) при x=2; y=Ö3:

А) 2^Ö3; Б) Ö2; В) 4; Г) 8.

 

Вариант 4.

1. Выбрать наибольшее число:

А) (1/5)^-1,5; Б) 1; В) (1/5)^-1,7; Г) (Ö5)^-Ö3;

1. Найти наименьшее значение функции y=ê2^x-4êна отрезке [-2; 4]:

А) 3,75; Б) 0; В) 3; Г) 2.

1. Найти абсциссу точки пересечения графиков функций: y=(4/3)^2x+2 и y=(0,75)^3x-7:

А) 7; Б)-7; В)1; Г)-1.

1. Решить неравенство: 4^x-0,5*2^3x+3³Ö8:

А) [-0.1; +¥); Б) (-¥; 0.1]; В) (-¥; -0.1]; Г) [0.1; +¥).

1. Найти сумму корней уравнения: (0.2)^x²*5^2x+2=(1/5)⁶:

А) 4; Б) 2; В) -2; Г) -4.

1. Найти значение выражения: z=(x^(y+1)²:4^-y) при x=2; y=Ö3:

А) 2^Ö3; Б) Ö2; В) 4; Г) 8.

 

Тест №7.4

Вариант 1.

Уровень А.

А1. Какая функция является возрастающей:

А) y=0,2^x;

Б) y= 3^x;

В) y=(0,6)^x;

Г) y=2^-x.

А2. Найдите область значений функции y=3^x-6:

А) (-µ; +µ);

Б) [-6; +µ];

В) (0; +µ);

Г) (-6; +µ).

А3. Решите уравнение 81*3^x=1/9:

А) –2;

Б) –6;

В) 2;

Г) 3.

А4. Решите неравенство 8*2^1-x>4:

А) (-µ; 2);

Б) (0; +µ);

В) [2; +µ);

Г) (-µ; +µ).

А5. Найдите наибольшее из чисел:

А) (0,25)²;

Б) 1;

В) 4^-1;

Г) (0,25)^1,7.

Уровень В.

В1. Решить уравнение 9^x+2*3^x+1-7=0 (ответ: {0})

В2. Решить неравенство 2*2^2x-7*10^x+5*5^2x<0 (ответ: (-1; 0))

В3. Решить систему уравнений: ì2^x+2^x+3=9

í3^8x_ 9

î3^3y `1 (ответ: (0; -2/3))

Уровень С.

С1. Решить уравнение çx-3ê^3x²-10x+3=1 (ответ: {½; 2; 3; 4})

С2. Решить неравенство (x-0,5)^x-2,5<1 (ответ: xÎ(1,5; 2,5))

 

 

Вариант 2.

Уровень А.

А1. Какая функция является убывающей:

А) y=0,2^-x;

Б) y= 3^x;

В) y=(0,6)^x;

Г) y=22^x.

А2. Найдите область значений функции y=(¾)^x:

А) (-µ; +µ);

Б) [-6; +µ];

В) (0; +µ);

Г) (-6; +µ).

А3. Решите уравнение 2^½(x-1)=2(2^½):

А) –2;

Б) 4;

В) 2;

Г) 3.

А4. Решите неравенство (0,2)^3+x³0,04:

А) (-µ; -5];

Б) [-5; +µ);

В) [-1; +µ);

Г) (-µ;-1].

А5. Найдите наименьшее из чисел:

А) 4^1,9;

Б) (0,25)^-3;

В) 4²;

Г) 1.

Уровень В.

В1. Решить уравнение 5^x+1-2*5^x-1-23=0 (ответ: {1})

В2. Решить неравенство 3^2x+1+1<4*3^x (ответ: (-1; 0))

В3. Решить систему уравнений: ì3^y*2^x=972

í

îy-x=3 (ответ: (2; 5))

Уровень С.

С1. Решить уравнение çx-2ê^4-x²=1 (ответ: {-2; 1; 2; 3})

С2. Решить неравенство (x-2)^x-4<1 (ответ: xÎ(3; 4))

 

Вариант 3.

Уровень А.

А1. Какая функция является возрастающей:

А) y=(0,2)^x+1;

Б) y= (1,09)^x;

В) y=(0,9)^x;

Г) y=3^-x.

А2. Найдите область значений функции y=2^x+2:

А) (-µ; +µ);

Б) (2; +µ];

В) (-2; +µ);

Г) (0; +µ).

А3. Решите уравнение 8^-1*2^x+3=4:

А) –2;

Б) –6;

В) 2;

Г) 3.

А4. Решите неравенство 5^3-x<0,04:

А) (-µ; 5);

Б) (1; +µ);

В) (5; +µ);

Г) (-µ;1).

А5. Найдите наибольшее из чисел:

А) (0,(6))³;

Б) 1;

В) (1,5)^-1;

Г) (0,(6))^1,7.

Уровень В.

В1. Решить уравнение 49^x-8*7^x+7=0 (ответ: {0; 1})

В2. Решить неравенство 5^x²-1-5^x²-2>2^x²-1+2^x²+1 (ответ: (-Ö3;Ö3))

В3. Решить систему уравнений: ì3^x+2^y/2=7

í

î3^2x-2^y=77 (ответ: (2; 2))

Уровень С.

С1. Решить уравнение (sin x)^x=1 (ответ: {0; p/2+pn, nÎZ})

С2. Решить неравенство (x+0,2)^x-4<1 (ответ: xÎ(1,2; 4))

 

 

Вариант 4.

Уровень А.

А1. Какая функция является убывающей:

А) y=0,2^x;

Б) y= 3^x;

В) y=(7,6)^x;

Г) y=12^x.

А2. Найдите область значений функции y=(¾)^x:

А) (-µ; +µ);

Б) [-6; +µ];

В) (0; +µ);

Г) (-6; +µ).

А3. Решите уравнение 27^x-3=1/9:

А) –2;

Б) 4;

В) 1/3;

Г) 3.

А4. Решите неравенство (1/2)^3-x³1/32:

А) (-µ; -2];

Б) [-2; +µ);

В) [-1; +µ);

Г) (-µ;-1].

А5. Найдите наименьшее из чисел:

А) (1/2)^1,9;

Б) (1/2)³;

В) 2^-2;

Г) 1.

Уровень В.

В1. Решить уравнение 5*3^2x+2*15^x-3*5^2x=0 (ответ: {1})

В2. Решить неравенство 3^2/x-1+3^2/x-2³324 (ответ: (-¥; 1/3])

В3. Решить систему уравнений: ì3^2x+4^2y=82

í

î3^x-4^y=8 (ответ: (2; 0))

Уровень С.

С1. Решить уравнение x^sinx=1 (ответ: {1; pn, nÎZ})

С2. Решить неравенство (x-0,5)^x-4<1 (ответ: xÎ(0,5; 4))

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: