 |
Задания для самостоятельного изучения
|
|
|
|
Раздел: Основные понятия и методы математического анализа.
Задание:
1.Изучить материал, используя:
1).С.Г. Григорьев, С.В. Иволгина Математика, М: Издательский дом «Академия», 2013 (Глава 1. Дифференциальное и интегральное исчисление.)
2).http://www.cleverstudents.ru/limits/types_of_uncertainties.html
2.Ответьте на следующие вопросы:
1. Дайте определение функции с одной переменной.
2. Перечислите способы задания функции.
3. Понятие предела функции в точке, в бесконечности.
4. Сформулируйте определение производной функции.
5. Правила и формулы дифференцирования.
6. Понятие производной сложной функции.
7. Применение производной к исследованию функций и построению графиков.
8. Дайте определение неопределенного интеграла.
9. Чему равен неопределенный интеграл?
10. Как называется каждый элемент в обозначении неопределенного интеграла?
11. Что называется интегрированием функции?
12. Перечислить основные свойства неопределенного интеграла.
13. Таблица неопределенных интегралов.
14. В чем заключается метод непосредственного интегрирования при отыскании неопределенного интеграла?
15. В чем заключается метод замены переменной (метод подстановки) при отыскании неопределенного интеграла?
16. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл как предел интегральной суммы.
17. Производная интеграла по верхнему пределу. Формула Ньютона-Лейбница.
18. Приложение интегралов к вычислению площадей плоских фигур, длин дуг кривых, объемов тел. Физические приложения определенного интеграла.
3.Выполните тестовые задания:
1. Область непрерывности функции  имеет вид…
имеет вид…
1)(3;5) 2) 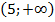 3)
3)  4)
4) 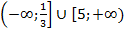
2. Предел 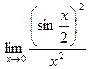 равен…
равен…
|
|
|
1) 2 2) 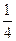 3) 1 4) ∞ 5) 0
3) 1 4) ∞ 5) 0
3. Количество точек разрыва функции 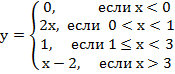 равно…
равно…
1) 2 2) 3 3) 1 4) 0 5) 4
4. Если 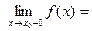
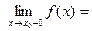
 , то функция
, то функция 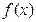 в точке
в точке 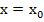 …
…
1)определена 2)ограничена 3)убывает 4)непрерывна 5)возрастает
5. Функция  имеет разрыв в точке…
имеет разрыв в точке…
1)5 2)-5 3)0 4)10 5)3
6. Физический смысл второй производной…
1)ускорение 2) скорость 3) масса 4) путь 5) сила
7. Дана функция  . Тогда
. Тогда  равно…
равно…
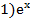 2) –
2) – 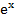 3) –
3) – 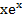 4) -3
4) -3 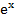 -
- 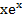 5)
5) 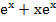
8. Геометрический смысл производной…
1)f '(x)= 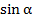 2) f '(x)=
2) f '(x)= 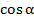 3) f '(x)=
3) f '(x)=  4) f '(x)=
4) f '(x)= 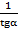 5) f '(x)=
5) f '(x)= 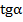
9. Закон движения материальной точки имеет вид х(t)=4+10t+e7-t, где х(t) – координата точки в момент времени t. Тогда скорость точки при t = 7 равна…
1)11 2) 9 3) 13 4) 75 5) 14
10. Найти производную функции: y= arcsin 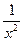
1) - 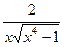 2)
2) 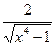 3)
3) 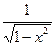 4)
4)  5) -
5) - 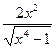
11. Уравнение касательной к кривой 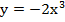 в точке А (1; -2) имеет вид…
в точке А (1; -2) имеет вид…
1) 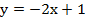 2)
2) 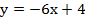 3)
3) 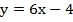
4)  5)
5) 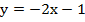
12. Уравнение наклонной асимптоты графика функции 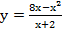 имеет вид
имеет вид 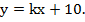 Тогда значение k равно…
Тогда значение k равно…
1)-2 2) 1 3) 4 4) -1 5) 8
13. Если при переходе через критическую точку производная f '(x) меняет знак с 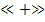 на
на
 , то в этой точке функция f(x) имеет…
, то в этой точке функция f(x) имеет…
1)максимум 2)нулевое значение 3)минимум 4)предел
14. Точка перегиба функции 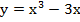 равна…
равна…
1)  2)
2) 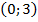 3)
3) 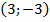 4)
4)  5)
5) 
15. Дифференциал третьего порядка функции 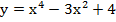 равен…
равен…
1) 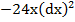 2)
2)  3)
3)  4)
4)  5)
5) 
16. Все элементарные функции в области определения…
1)возрастают 2)убывают 3)ограничены
4)имеют предел 5)непрерывны
17. Область определения функции 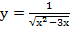 имеет вид…
имеет вид…
1)(0;3) 2)(-  3)
3)  4)
4) 
|
|
|
18. Предел 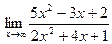 равен…
равен…
1)  2) 2,5 3) ∞ 4) 0 5) 2
2) 2,5 3) ∞ 4) 0 5) 2
19. Количество точек разрыва функции 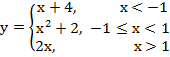 равно…
равно…
1) 2 2) 3 3) 1 4) 0 5) 4
20. Если в точке 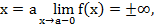 то это точка…
то это точка…
1)разрыва 1 рода 2) скачка функции
3)разрыва 2 рода 4)устранимого разрыва
21. Физический смысл первой производной…
1)ускорение 2) скорость 3) масса 4) путь 5) сила
22. Дана функция 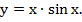 Тогда у"+у равно…
Тогда у"+у равно…
1) 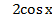 2)
2) 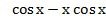 3)
3) 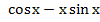
4) 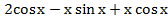 5) 2
5) 2 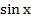
23. Тангенс угла наклона касательной к кривой 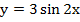 в точке
в точке 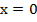 равен…
равен…
1) 3 2)-3 3)-6 4)6 5)0
24. Закон движения материальной точки имеет вид х(t)=4 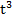 +10t, где х(t) – координата точки в момент времени t. Тогда ускорение точки при t = 3 равно…
+10t, где х(t) – координата точки в момент времени t. Тогда ускорение точки при t = 3 равно…
1)46 2) 138 3) 12 4)72 5) 24
25. Найти производную функции: y = 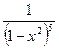
1)  2)
2) 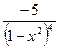 3)
3) 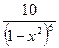 4)
4)  5)
5) 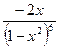
26. Уравнение касательной к кривой y= 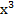 в точке А(0;0) имеет вид…
в точке А(0;0) имеет вид…
1) y-2x=1 2) y=2x+2 3) y=0 4) y-1=0 5) y=2x
27. Если при переходе через критическую точку производная f '(x) меняет знак с  на
на
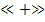 , то в этой точке функция f(x) имеет…
, то в этой точке функция f(x) имеет…
1)максимум 2)нулевое значение 3)минимум 4)предел
28. Дифференциал второго порядка функции 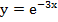 равен…
равен…
1)  2)
2) 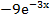 3)
3) 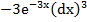 4) 9
4) 9  5)
5) 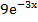
29. Уравнение наклонной асимптоты графика функции 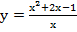 имеет вид
имеет вид  Тогда значение k равно…
Тогда значение k равно…
1)-2 2) 1 3) 4 4) -1 5) 2
30. Если в интервале 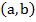 f "(x)
f "(x) 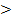 0, то в этом интервале график функции…
0, то в этом интервале график функции…
1)вогнутый 2)выпуклый 3)возрастает 4)убывает
(Ответы: 1(3); 2(2); 3(2); 4(4); 5(1); 6(1); 7(3); 8(5); 9(2); 10(1); 11(2); 12(4); 13(1); 14(5); 16(5); 17(2); 18(2); 19(1); 20(3); 21(2); 22(1); 23(4); 25(1); 26(3); 27(3); 28(1); 29(2); 30(1))
|
|
|


