По выполнению контрольных работ

Задание1: Вычислить пределы.

 

а) lim 7х²+6х+1         б) lim х – 7      в) lim sin 20x           

^х→∞ 6х² – х               ^х→7 х² - 49              ^х→0 tg 7x                      

 

Решение:

а) Имеем lim 7х²+6х+1 = (неопределенность вида ∞/∞, разделим числитель и    

              ^х→∞ 6х² – х   знаменатель дроби на старшую степень х)

 

= lim 7х²/х² + 6х/х² + 1/х²  = lim 7 + 6/х + 1/х²  = 7 + 0 + 0   = 7          

  ^х→∞  6х²/х² – х/х^{2       х→∞} 6 – 1/х            6 – 0     6

 

б) Имеем lim х – 7   = (неопределенность вида 0/0, разложим на множители

             ^х→7 х² - 49                               знаменатель дроби и сократим)

= lim       х – 7  = lim     1  =   1  = 1    

^х→7 (х – 7)(х+7) ^х→7 х + 7 7+7 14

 

в) lim sin 20x = (воспользуемся первым замечательным пределом lim sin x  = 1)

^х→0 tg 7x                                                                                        ^х→0 x

= lim     sin 20x    = lim sin 20x cos 7x = lim sin 20x lim cos 7x = (lim cos 7x = 1)

^х→0  sin 7x/cos7x     ^х→0       sin 7x         ^х→0 sin 7x    ^х→0 7x    ^х→0 7x

= lim sin 20x 20x 7x = lim sin 20x lim   7x   lim 20x = 1·1· 20 = 20

^х→0 20x sin 7x 7x ^х→0 20x  ^х→0 sin 7x ^х→0 7x         7 7

Задание 2. Найти производную а) у = 8х⁵ + 2х² – 14х – 222

                                                      б) y = (x+1)· cos x

                                                      в) y = x + 7

                                                                 x – 3

                                                      г) y = (5x² +2x)⁷

Решение:

а) Воспользуемся формулой производной степенной функции (xⁿ)' = n(x) ^n-1

и следующими правилами дифференцирования: (u+v)' = u' + v'

                                                                              (C u)' = C(u)'

у' = (8х⁵ + 2х² – 14х – 222)' = 8(х⁵)'+ 2(х²)' – 14(х)' – (222)' =

 = 8·5x⁴ + 2·2x – 14·1 – 0 = 40x⁴ + 4x – 14

 

б) Воспользуемся формулой производной произведения (u·v)' = u'·v + u·v'

y' = ((x+1)· cos x)' = (x+1)' cosx + (x+1) (cosx)' = cos x + (x+1)(- sin x)

 

в) Воспользуемся формулой производной частного (u)' = u '· v – u·v '

                                                                                   v        v²

 y' = x + 7 ' = (x+7)'(x – 3) – (x+7)(x – 3)' = 1·(x – 3) – (x+7)·1 = x–3–x–7 =   - 10

    x – 3                    (x – 3)²                      (x – 3)²               (x – 3)² (x – 3)² 

 

г) Воспользуемся формулой производной сложной функции  (u(v))' = u'·v'

 

y' = ((5x² +2x)⁷) ' = 7(5x² +2x)⁶(5x² +2x) ' = 7 (5x² +2x)⁶ (10х+2)

Задание 3. Исследовать методами дифференциального исчисления функцию и построить ее график:    y = 3х – х³ – 1

 

Решение:

Для исследования функции и построения ее  графика воспользуемся схемой:

1. Найти область определения функции;
2. Проверить четность, нечетность, периодичность функции;
3. Найти нули функции, точки пересечения графика с осями координат (если это возможно)
4. Найти асимптоты графика функции;
5. Найти промежутки возрастания и убывания функции, ее экстремумы;
6. Найти промежутки выпуклости и вогнутости, точки перегиба;
7. Построить график функции, используя результаты исследования.

Для более точного построения можно найти дополнительные точки графика, вычислив значения функции в некоторых точках.

       Реализуем указанную схему.

1) О.О.Ф.      х – любое число

2) Проверим четность: у(-х) = 3(-х) – (- х)³ – 1 = - 3х + х³ – 1                        не выполняется равенство у(-х) = - у(х) функция не является нечетной

не выполняется равенство у(-х) = у(х) функция не является четной

Функция не является периодичной.

3) Точка пересечения с осью ОУ (0; -1), так как у(0) = -1.                                    Точек пересечения с осью ОХ                                                                    

1)  Найдем асимптоты графика функции:                                                         Точек разрыва функция не имеет, значит вертикальных асимптот нет. Предел функции на бесконечности lim f(x) = ∞

                      ^{х→ ±∞}

горизонтальных асимптот нет.

Проверим наличие наклонных асимптот для графика функции у = f(x)

 

k = lim f (x) = lim 3х – х³ – 1 = lim 3 – х² – 1/х = 3 - ∞ - 0 = - ∞   

    ^{х→ ±∞} х        ^{х→ ±∞}  х         ^{х→ ±∞}

наклонных асимптот нет    

2) Найдем экстремумы функции, для этого найдем первую производную функции у' = (3х – х³ – 1)' = 3 – 3х²

Стационарные точки: 3 – 3х² = 0

                                  х² = 1

                                            х = ± 1                            

      у(-1) = - 3; у(1) = 1                                                          

Функция убывает (-∞; -1) и (1; +∞), возрастает (-1; +1)

3) Найдем промежутки выпуклости и вогнутости, для этого найдем вторую производную у'' = (3 – 3х²)' = - 6х                                                                  точки перегиба у'' = 0 → х = 0                                   _______________________

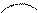У(0) = - 1                                                              0

 

 

4) Строим график:

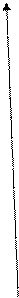                                           у

 

                           

 

                                                        

 

-1        1                     х       

 

 

  

Задание4. Найти неопределенный интеграл

А)ò (2х³+9х²+10)dx     Б) ò (2x +1)²⁴dx      В) ò x sin2x dx

Решение:

А) Для нахождения интеграла используем прием непосредственного интегрирования, и формулу первообразной степенной функции

ò (2х³+9х²+10)dх=2·х³⁺¹/(3+1)+9х²⁺¹/(2+1)+10х=2·х⁴/4+9х³/3+10х=х⁴/2+3х³+10х+C

Б) Для нахождения интеграла используем прием замены переменной, и формулу первообразной степенной функции.

Заменим 2х+1 = t, тогда dt = d(2x+1) = 2 dx, тогда dx = ½ dt,           подставляя в исходный интеграл имеем:

ò (2x +1)²⁴dx = ò1/2 t²⁴ dt = 1/2· t²⁵/25 = (2x+1)²⁵/50 + C

В) Для нахождения интеграла используем прием интегрирования по частям

ò u dv = uv - ò v du

ò x sin2x dx = [ x = u sin 2x dx = dv ] = -½x cos 2x - ò(-½cos2x) dx=

                      dx = du òsin 2xdx = ò dv

                                      -½ cos 2x = v

 = -½x cos 2x + ½ ½sin 2x = -½x cos 2x + ¼sin 2x + C

Задание 5. Вычислить определенный интеграл

₃

∫(x²+2)dx

¹

Решение:

       Определенный интеграл вычисляется по формуле Ньютона-Лейбница

                                                               

_{b                                b}

ò f(x) dx = F(x)ô = F(b) – F(a)

^{a                                  a}

_{3                                                           3}

∫(x²+22)dx = (x³/3 + 22x)ô= (3³/3 + 22·3) – (1³/3 + 22·1) = (9 + 66) – (0,3 + 22) =

^{1                                                           1}             = 75 – 22.3 = 52.7

 

Задание 6. Вычислить площадь фигуры, ограниченной линиями:

                               у=х²+4, у=6 – х.                               Сделать рисунок.

Решение:

Найдем точки пересечения графиков, для этого решим уравнение

         х²+4 = 6 – х

         х²+ х – 2 = 0, откуда х₁ = - 2; х₂ = 1 – границы интеграла.

Линия у = 6 – х лежит выше графика функции у = х²+4, поэтому находим площадь фигуры как разность площадей криволинейных трапеций.

   _{1                                                          1                                                                                         1}

S = ò((6 – x) – (x²+4)) dx = ò(2 – x – x²) dx = (2x – x²/2 – x³/3)ô= (2·1 – 1²/2 – 1³/3) –   

   ^{-2                                                   -2                                                                                 -2}

- (2·(-2) – (-2)²/2 – (-2)³/3) = (2 - 0,5 – 0,3) – (- 4 – 2 +2,7) = 1,2 – (-3,3) = 4,5

 

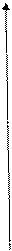Сделаем рисунок:                          у

 

 

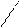
                                                        6

                                                        4

 

                                        

Ответ: S = 4,5 кв.ед.

 

 

Задание 9. {\displaystyle \int \limits _{a}^{b}f(x)\,dx\approx {\frac {b-a}{n}}(y_{0}+y_{1}+\ldots +y_{n-1}).}  Какую работу надо затратить, чтобы насыпать кучу песка конической формы с радиусом основания R и высотой H. Плотность песка ρ.

Решение: 

В результате рассмотрения задачи можно получить, что искомая работа равна:

Из некоторых соображений найдем работу, которую нужно совершить, чтобы насыпать кучу до половины высоты, то есть в качестве верхнего предела возьмем Н/2.

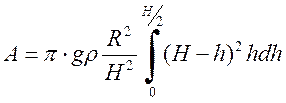
Возьмем интеграл аналитически:

 

 

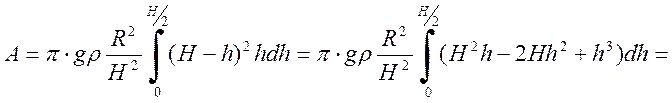
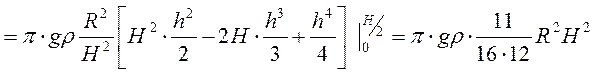
Основная литература.

1. Бутузов В.Ф., Крутицкая Н.И. Математический анализ в вопросах и задачах. – М.: Физматлит, 2009г.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 1 и 2. – М.: ОНИКС 21 век «Мир и Образование», 2008 г.
3. Пехлецкий И.Д. Математика: учебник. – М.: Издательский центр «Академия», Мастерство, 2012 г.

 

Дополнительная литература.

1. Выгодский М.Я. Справочник по высшей математике. – М.: Роскнига, 2001 г.
2. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2003.
3. Натансон И.П. Краткий курс высшей математики. С-Пт.:Лань, 2001 г.
4. Подольский В.А. и др. Сборник задач по математике: учебное пособие для средних специальных учебных заведений. М.: Высшая школа, 1999 г.

 

Приложение 1.

1234	Поделиться:

Воспользуйтесь поиском по сайту: