Измерение вариации признака

Для измерения вариации признака применяют такие показатели, как:

- вариационный размах;

- дисперсии;

- среднее квадратическое отклонение;

- относительный коэффициент вариации.

Вариационный размах (R) (широта распределения) – это показатель, характеризующий разность между крайними значениями вариационного ряда:

R = x_max – x_min, (7)

где x_max и x_min – варианты вариационного ряда.

Например, вариационный размах для ряда, характеризующего число осужденных за тяжкие телесные повреждения (таблица 1) составляет R = 26 -16 = 10 лет.

Но, несмотря на простоту рассматриваемого критерия вариации признака (R), при практическом использовании он чрезвычайно зависит от случайностей, весьма неустойчив и поэтому может служить лишь для грубой оценки колеблемости вариационного ряда.

Более надежным и наиболее часто применяемым на практике, хотя и более сложным для вычисления, являются показатели дисперсии и среднего квадратического отклонения.

Дисперсия вычисляется по формуле:

(8)

Например, дисперсия показателя возраста осужденных за тяжкие телесные повреждения (вариационный ряд в таблице 1) равна 6,02.

Среднее квадратическое отклонение (σ) является производным от дисперсии. Рассчитывается среднее квадратическое отклонение по формуле:

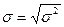(9)

Для рассматриваемого примера σ = 2,45.

Очевидно, что чем больше показатели вариации признака, в частности, дисперсия, тем менее однородна исследуемая совокупность социально-правовых явлений.

С учетом того, что среднее квадратическое отклонение представляет собой абсолютную величину и зависит от единицы измерения, для сопоставимости различных исследований нужно использовать относительный коэффициент вариации.

Относительный коэффициент вариации (V) – это коэффициент, представляющий собой отношение среднего квадратического отклонения от средней арифметической, выраженное в процентах:

(10)

Значение относительного коэффициента вариации применительно к возрастному распределению осужденных за тяжкие телесные повреждения (таблица1) равно 12,2%.

В практике социально-правовых исследований довольно часто встречаются случаи, когда при анализе вариационного ряда числовое значение того или иного признака резко выделяется, вызывая большие сомнения с точки зрения включения его в дальнейшую обработку.

Причинами такого положения могут быть следующие:

- в первичном материале произошла грубая ошибка (ошибку необходимо исправить);

- значительное отличие варианты от других, когда ее значение выходит за пределы случайной вариации (варианту следует исключить из рассмотрения как ошибочную).

Но нередко бывает и такая ситуация, когда вызвавший сомнение объект, характеризующийся маловероятным значением признака, на самом деле является уникальным и должен быть повергнут индивидуальному социально-правовому анализу.

Таким образом, исключение вариантов не должно быть автоматическим, его следует производить с большой осторожностью.

При исключении испытуемого варианта из вариационного ряда следует следовать следующему алгоритму:

Шаг 1. Вычислить среднюю арифметическую без включения в нее признаков испытуемого варианта x_R.

Шаг 2. Вычислить вариационный размах R без включения признаков испытуемого варианта.

Шаг 3. Определить, заключается ли величина испытуемого варианта (S) в следующих пределах:

, (11)

где коэффициент α находится из таблицы 3:

Таблица 3.

Зависимость значения коэффициента α

от объема исследуемой совокупности

Объем исследуемой совокупности, n				8-9	10-11	12-15	16-22	23-35	36-63	64-150	151-330
Коэффициент α	1,7	1,6	1,5	1,4	1,3	1,2	1,1	1,0	0,9	0,8	0,7

 

Пример использования алгоритма исключения испытуемого варианта из вариационного ряда.

Постановка задачи. Пусть имеется вариационный ряд: распределение времени, затраченного дежурной группой для достижения места происшествия (таблица 4):

Таблица 4.

Эмпирическое число поездок и теоретические частоты

Время, затраченное дежурной группой для достижения места происшествия, xi, мин	Эмпирическое число поездок (частота), ni*	Теоретические частоты, niT
2,5
3,0
3,5
4,0
4,5
5,0
5,5
6,0
6,5
7,0
7,5
8,0
8,5
9,0
20,0
Итого:

Сомнение вызывает варианта 20,0.

Средняя арифметическая равна 5,59.

Вариационный размах R = 6,5 при n = 112 и α = 0,8.

Таким образом, допустимые границы вариации определяются соотношением:

0,39 < S < 10,79.

Так как варианта 20,0 почти в два раза превосходит максимально допустимую границу случайного колебания, то при дальнейшей обработке вариационного ряда ее надо исключить.

Графическое представление вариационного ряда в виде полигона принято называть также эмпирической кривой распределения.

Для обеспечения анализа, предсказания различных свойств исследуемой совокупности стремятся описать эмпирический ряд с помощью некоторой математической модели – закона распределения.

Самым известным законом распределения в природе и обществе, в частности, проявляющимся в действии социально-правовых процессов, выступает закон нормального распределения.

Кривая функции плотности нормального распределения описывается с помощью следующего соотношения:

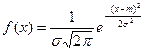(12)

Нормальное распределений той или иной случайной величины возникает в силу влияния на нее большого числа случайных причин, не имеющих значительного преимущества в этом влиянии друг перед другом. Такими случайными величинами могут выступать:

- возраст преступников;

- количество сигналов о происшествиях за единицу времени;

- время раскрытия преступления и др.

Покажем, что эмпирический вариационный ряд, отражающий время, затрачиваемое дежурной группой для достижения места преступления (таблица 4), подчиняется закону нормального распределения.

Средняя арифметическая этого ряда (математическое ожидание – m) равна 5,64.

Среднее квадратическое отклонение σ = 1,26.

Подставляя известные значения в формулу для функции плотности нормального распределения (формула 12), получим формулу конкретного эмпирического нормального распределения времени:

f(x)^* = 0,316* exp (- 0,313 * (x – 5,64)²). (13)

Для получения теоретических частот нормального распределения (n_i^T), то есть вычисленных с помощью математической модели частоты нормального распределения, необходимо значение функции f(x)^* умножить на k*n, то есть:

n_i^T = f(x)^*k*n. (14)

Этим самым учитывается величина выборочной совокупности и интервал наблюдения эмпирических данных.

Применительно к рассматриваемому примеру (исходные данные в таблице 4), получим формулу конкретного теоретического нормального распределения времени:

f(x) = 17,5* exp (- 0,313 * (x – 5,64)²). (15)

Результаты расчетов приведены в правом столбце таблицы 4, где в нижней строке представлены значения теоретических частот, вычисленных по формуле (15).

В том, что эмпирическая и теоретическая функции плотности распределения выездов дежурных групп примерно совпадают (то есть теоретическое нормальное распределение достаточно верно отражает эмпирическое распределение исследуемой совокупности), можно убедиться, построив график распределения выездов дежурных групп по времени достижения места происшествия (график строится самостоятельно). На графике по оси абсцисс откладывается время (от 0 до 10 мин.), а по оси ординат – количество выездов (от 0 до 20).

На графике можно увидеть, что кривая нормального распределения располагается симметрично относительно средней арифметической, поэтому величину средней называют центром распределения.

Влияние величины среднего квадратического отклонения (σ) сказывается следующим образом:

- чем σ меньше, тем более вытянута кривая вдоль оси ординат;

- чем σ больше, тем более плоской становится кривая, растягиваясь вдоль оси абсцисс.

Для практических приложений в социально-правовых исследованиях используется правило «трех сигм»:

- случайная величина с нормальным распределением практически не принимает значений, которые отличаются от средней арифметической на величину больше, чем 3 σ.

Если указать точнее, то:

- в интервал (+-) σ попадает 68% всех наблюдений;

- в интервал (+-)2 σ попадает 96% всех наблюдений;

- в интервал (+-)3 σ попадает 99,7% всех наблюдений.

Если проанализировать самостоятельно построенный график для рассматриваемого примера, то можно убедиться, что в интервал (+-)2 σ попало 93,8% всех выездов дежурных групп. Таким образом и интервала (+-)2 σ достаточно, чтобы оценить основное число вариант в исследуемых совокупностях, характеризующих те или иные социально-правовые процессы.

Важно знать, что при нормальном распределении величины средней арифметической, моды и медианы совпадают.

⇐ Предыдущая20212223242526272829Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: