 |
Определение объема выборки
|
|
|
|
На практике часто возникает вопрос «Какой объем должна иметь выборка, чтобы получить результаты нужной точности?».
Конечно, чем большее количество первичного материала имеет исследователь, тем не хуже. Однако из практики социально-правовых исследований известно, что чем больше первичного материала, тем больше необходимо провести вычислений, и, соответственно увеличиваются затраты на получение и обработку этого материала.
Поэтому целесообразно ориентироваться на тот минимальный объем, который экономичен и дает возможность получить удовлетворительные результаты.
Объем выборки в существенной мере зависит от способа организации выборки.
Различают следующие способы отбора выборочных данных:
- собственно случайный отбор;
- механический отбор;
- типический отбор;
- серийный (гнездовой) отбор;
- комбинированный отбор.
Наиболее доступным и распространенным является собственно случайный отбор.
1. Собственно случайный отбор.
Этот способ означает выборку конкретных единиц из генеральной совокупности без дробления генеральной совокупности на группы. При этом существуют два варианта отбора:
- повторный (отобранная единица вновь участвует в последующей процедуре отбора);
- бесповторный (отобранная единица не участвует в последующей процедуре отбора).
Примеры:
1) в архиве суда тома уголовных дел отбираются и откладываются в сторону – это бесповторная выборка;
2) в архиве суда тома уголовных дел отбираются по их номеру несколькими независимыми экспертами – это повторная выборка.
Целями выборочного исследования могут быть:
а) изучение некоторых средних характеристик:
- средний срок осуждения;
- количество судимостей;
|
|
|
- средний возраст освобождающихся из мест лишения свободы и др.;
б) изучение долей определенных категорий в генеральной совокупности:
- доля рецидивистов среди содержащихся в исправительно-трудовой колонии строгого режима;
- доля осужденных за кражи;
- доля ложных сигналов в дежурную часть органа внутренних дел и др.
В зависимости от цели социально-правового исследования различаются и формальные соотношения для объема проектируемой выборки
Соотношения для определения объема выборки
| Способ отбора | ||
| Повторный | Бесповторный | |
| Изучение средних величин |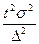 
| 
|
| Изучение долей |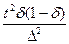 
| 
|
В таблице приняты следующие обозначения:
σ – среднее квадратическое отклонение;
δ – доля определенных элементов в генеральной совокупности;
N – объем генеральной совокупности;
Δ – требуемая точность оценки характеристик генеральной совокупности;
t - параметр, связанный с вероятностью, надежностью получения оценки.
В связи с тем, что величины σ и δ априори неизвестны, рекомендуется брать их приближенные оценки, полученные в других исследованиях или наблюдениях.
В частности, если даже приблизительно неизвестна доля изучаемых элементов в генеральной совокупности, то следует вместо произведения
δ(1- δ) подставить в формулы для объемов выборки его максимальное значение, равное 0,25. В этом случае соотношения во второй строке таблицы 5 примут вид:
- для повторной выборки;
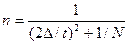- для бесповторной выборки
При очень больших (более 1000 единиц) объемах генеральной совокупности формулы для повторной и бесповторной выборок практически совпадают.
При вероятности (надежности) 0,95 обеспечения заданной точности выборочных оценок t = 2, а при вероятности 0,99 - t = 3.
В социально-правовых исследованиях, как правило, надежность в 95% является вполне приемлемой.
Пример 1 проектирования выборочного наблюдения.
|
|
|
Пусть необходимо определить средний срок расследования преступлений в N-ом управлении внутренних дел.
Требуемая точность Δ – одна неделя.
Общее число уголовных дел в последний год – 15000.
Требуемая надежность – 95% (то есть t = 2).
Произведенные пробные выборки дали приближенную оценку для дисперсии σ2 = 49.
По формуле для бесповторной выборки применительно к средним величинам получаем объем выборочной совокупности для указанных условий n = 194 (проверить самостоятельно).
Поскольку объем генеральной совокупности достаточно велик, то можно воспользоваться более простой формулой для повторной выборки. В этом случае n = 196 (проверить самостоятельно).
Пример 2 проектирования выборочного наблюдения.
Пусть необходимо провести выборочное наблюдение для оценки доли осужденных за кражи, содержащихся в колонии общего режима с фактической наполняемостью в 1200 человек.
Если никаких предварительных данных о размере этой доли не имеется то произведение δ(1- δ) в формуле таблицы 5 заменяем на 0,25.
Требуемая точность определения доли – 5% с надежностью 0,95.
Воспользовавшись выражением (19) для бесповторной выборки, оцениваем ее объем n = 303.
Основной принцип организации собственно-случайной выборки – это обеспечение равной возможности быть отобранным каждому элементу генеральной совокупности. Для этого используются таблицы случайных чисел или датчики случайных чисел для ЭВМ.
2. Механический отбор.
При механическом отборе генеральная совокупность «механически» делится на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект.
Например, если нужно отобрать для анализа личности правонарушителя 20% уголовных дел, связанных с совершением тяжких телесных повреждений, то отбирают каждое пятое дело; если требуется отобрать 5% уголовных дел, то отбирают каждое двадцатое.
Можно пронумеровать элементы генеральной совокупности, а затем в зависимости от объема выборки, установив шаг отбора, произвести их отбор.
Иногда механический отбор может не обеспечить репрезентативность выборки.
3. Типический отбор.
При типическом отборе генеральная совокупность по тому или иному признаку делится на типические группы таким образом, чтобы максимально уменьшить в каждой типической группе колеблемость признака.
|
|
|
Количество единиц из каждой типической группы выбирается пропорционально среднему квадратическому отклонению признака в этой группе.
При типическом отборе получаются более точные результаты, чем при механическом отборе.
4. Серийный (гнездовой) отбор.
При серийном отборе генеральную совокупность делят на ряд групп (серий), а затем случайным образом производят выборку из них. Серии, попавшие в выборку, обследуются сплошным образом.
Серийная выборка применяется в том случае, когда сложно организовать выборочное наблюдение путем собственно случайного отбора, механического отбора или типического отбора в силу ограниченности ресурсов (людских, материальных и др.) участников выборочного наблюдения.
Пользуются серийным отбором тогда, когда обследуемый признак колеблется в различных сериях незначительно.
5. Комбинированный отбор.
При комбинированном отборе отбор проводится следующим образом:
- на первом этапе проводится выборочный отбор серий одинакового объема;
- на втором этапе простым случайным отбором выбирают несколько серий;
- на третьем этапе из каждой серии простым случайным отбором извлекают отдельные объекты, то есть выборочный отбор единиц из этих серий.
Оценки вариационного ряда могут быть:
- точечными;
- интервальными.
Точечной называют оценку, определяемую одним числом.
При выборке малого объема точечная оценка может существенно отличаться от оцениваемого параметра, и, как следствие, приводит к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальной называют оценку, определяемую двумя числами – концами интервала.
Интервальная оценка, в отличие от точечной, позволяют установить:
- точность оценок;
- надежность (доверительную вероятность) оценок.
Точностью оценки называют некоторое положительное число δ, с помощью которого можно определить абсолютную величину разности между действительным значением неизвестного параметра R и найденной по данным выборки статистической характеристикой (R*), служащей оценкой этого неизвестного параметра R. То есть если δ > 0 и | R – R* | < δ, то, чем меньше δ, тем оценка точнее.
|
|
|
Однако статистические методы не позволяют категорически утверждать, что оценка R* удовлетворяет неравенству | R – R* | < δ. Можно говорить лишь о некоторой вероятности γ, с которой это неравенство выполняется.
Поэтому при интервальной оценке вводят понятие надежности (доверительной вероятности) оценки.
Надежностью (доверительной вероятностью) оценки R по R* называют вероятность γ, с которой осуществляется неравенство | R – R* | < δ.
Обычно надежность оценки задается наперед, причем в качестве γ берут значение, близкое к 1 (обычно это: 0,95; 0,99; 0,999).
Пусть вероятность того, что | R – R* | < δ, равна γ:
P[ | R – R* | < δ] = γ.
Если в этом соотношении заменить неравенство | R – R* | < δ равносильным ему двойным неравенством:
- δ<R – R* < δ, или R* - δ < R< R* + δ, то получаем:
P[R* - δ < R< R* + δ]= γ.
Полученное соотношение следует понимать так:
- вероятность того, что интервал (R* - δ, R* + δ) заключает в себе (покрывает) неизвестный параметр R, равна γ.
Интервал (R* - δ, R* + δ), покрывающий неизвестный параметр с заданной надежностью γ называют доверительным интервалом.
Интервал (R* - δ, R* + δ) имеет случайные концы (их называют доверительными границами). В разных выборках получаются различные значения R*, следовательно от выборки к выборке будут изменяться и концы доверительного интервала, то есть доверительные границы сами являются случайными величинами – функциями от x1, x2,…,xn.
А так как случайной величиной является не оцениваемый параметр R, а доверительный интервал, то правильнее будет говорить не о вероятности попадания R в доверительный интервал, а о вероятности того, что доверительный интервал покроет R.
2.1. Пример построения вариационного ряда при дискретной и непрерывной вариации.
Основные черты социальных и социально-правовых систем - это случай и время, то есть они развиваются во времени отчасти при непредсказуемом поведении их элементов.
Как мы уже знаем, изучение уголовно-правовых массовых явлений начинается со сбора статистических данных, то есть со статистического наблюдения.
Также нам известно, что полученный в результате наблюдения первичный материал подвергается в дальнейшем группировке, то есть равносоставную массу элементов разделяют по тому или иному признаку на однородные группы.
Пусть в качестве изучаемого признака (X) совокупности лиц, осужденных за тяжкие телесные повреждения, взят возраст.
|
|
|
Анализ возрастных способностей названной группы применительно к 55 осужденным дал следующие результаты:
16, 22, 20, 19, 18, 24, 21, 17, 23, 18,
19, 16, 22, 18, 23, 20, 19, 22, 20, 19,
20, 18, 21, 18, 19, 24, 17, 16, 23, 19,
25, 21, 20, 18, 19, 22, 20, 18, 17, 21,
19, 20, 23, 25, 22, 20, 17, 24, 19, 17,
21, 18, 19, 21, 26
На основе полученного статистического наблюдения может быть составлен следующий вариационный ряд (таблица 1):
Таблица 1.
| Возраст в годах, xi | |||||||||||
| Число осужденных, ni |
Объем выборки n = 55.
Изменение (вариация) признака может быть:
- дискретной;
- непрерывной.
При дискретной вариации значения признака отличаются друг от друга на некоторое (обычно целое) число, например:
- число судимостей;
- число сообщений о происшествиях, поступивших в дежурную часть;
- число эпизодов в уголовном деле и др.
При непрерывной вариации значения признака могут отличаться на сколь угодно малую величину, например:
- время достижения патрульной группой места происшествия;
- процент выполнения нормы выработки на предприятиях исправительно-трудовых учреждений (ИТУ) и др.
При непрерывной (а часто и при дискретной) вариации разделение признака называется интервальным, то есть частоты относятся не к отдельному значению признака, а к некоторому интервалу, например, вариационный ряд распределения работающих в ИТУ по норме выработки (таблица 2):
Таблица 2.
| Выполнение норм выработки в ИТУ (интервалы), % | 65-70 | 70-75 | 75-80 | 80-85 | 85-90 | 90-95 | 95-100 | 100-105 | 105-110 | 110-115 |
| Число работающих, ni |
Объем выборки n = 696.
Вариационные ряды могут быть и с одинаковыми и неодинаковыми интервалами.
От выбора интервала во многом зависят результата последующего анализа:
- при чрезмерно зауженном интервале начинает значительно сказываться случайность наблюдений, различные «шумовые» эффекты;
- при неоправданном расширении интервала нивелируются важные особенности наблюдаемого социально-правового явления.
От этих неприятных последствий уходят путем выбора интервала по формуле:
(1)
где: xmax - xmin – размах вариации, характеризующий разность между наибольшей и наименьшей вариантами;
n – объем выборки.
Для данных таблицы 1 получаем величину интервала k = 1,3; а для данных таблицы 2 k = 3,8.
Полученные значения близки к выбранным, то есть к интервалам 1 и 5 соответственно.
Относительный коэффициент вариации (V) – это коэффициент, представляющий собой отношение среднего квадратического отклонения от средней арифметической, выраженное в процентах:
(10)
|
|
|
