Приложение 1. Нумерация формул

Пример 1. Место номера при переносе формулы

 

 

(12)

 

 

Пример 2. Нумерация группы формул, расположенных отдельными строками

                                                      (3.4)

 

 

Пример 3. Нумерация группы формул — системы уравнений

                                     (5.6)

Пример 4. Нумерация формул — разновидностей основной формулы

(12а), (12б)… и т.д.

Пример 5. Нумерация промежуточных формул,

Не имеющих самостоятельного значения

(а), (б), (в), (*), (**), (***) ….

 

Пример 6. Двойная индексационная нумерация формул

 (3.7) — 7-я формула в гл. III;                    (9.5) — 5-я формула в § 9

 

 

Пример 7. Тройная индексационная нумерация формул

(7.9.6) — 6-я формула в § 9 гл. VII.

 

 

Приложение 2. Ссылки на номера формул в тексте

 

Пример 1. Основная форма ссылки

в формуле (3.4);       из уравнения (15.6) вытекает       и т.п.

 

Пример 2. Вариант ссылки без определяющего слова перед номером

Рекомендуется:                                      Не рекомендуется:

 

Из формулы (7.8) следует....                      Из (7.8) следует …

 

 

Пример 3. Ссылка на формулу в тексте, заключенном в скобки

Используя выражение для дивергенции [см. формулу (19.1)], получаем.....

 

 

Приложение 3. Пунктуация в тексте с формулами

 

 

Пример 1. Двоеточие перед формулой

а) …из формул сложения следуют формулы двойного аргумента:

sin 2 α = 2 sin cos α,

cos α = cos ² α – sin ² α, …

                                                                и т.д.

 

 

б) …разделив почленно последние два равенства, получим:

Приложение 4. Экспликация к формуле

Пример 1. Пунктуационное оформление текста с формулой и экспликацией

 

 

Индуктивность многослойной катушки определяется по формуле

 

 

 где w – число витков;

D – средний диаметр намотки, мм;

l – длина намотки, мм;

h – высота намотки, мм.

 

Приложение 5. Оформление записи формулы

Пример 1. Скобки

Пример 2. Скобки

Пример 3. Скобки

Пример 4. Коэффициенты

 

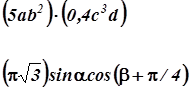
Пример 5. Употребление точки на средней линии как знака умножения

Точку ставят:

а)     ;    ;

б)     ;

в)     ;

г)     ;

д)    .

Пример 6. Употребление точки на средней линии как знака умножения

Точку не ставят:

а)           ;

б)    

в)     ;

г)     ;        ;     ab ln y.

д)    .

Пример 7. Употребление точки на средней линии как знака умножения

Рекомендуется:                                                        Не рекомендуется:

                                      

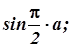
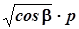
Пример 8. Употребление косого креста как знака умножения

а) площадь комнаты:

б)   .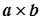

Пример 9. Многоточие в ряду перечисляемых, складываемых, приравниваемых символов

 

a₁  + а ₂  +... + а _n;              b₁ = b₂  =... = b_m.

 

Пример 10. Многоточие между перемножаемыми символами

 

                                      

 

Пример11. Многоточие и отточие в системах уравнений, матрицах, определителях

Приложение 6. Переносы в формулах

Пример 1. Перенос дроби с длинным числителем и коротким знаменателем

Дробь ;

можно привести к виду     

или, если использовать косую черту к виду A = (a ₁ x ₁ + a ₂ x ₂ + … + a_nx_n)/(p + q)

Пример 2. Перенос дроби с коротким числителем и длинным знаменателем

Дробь             

можно привести к виду, если использовать косую черту,         

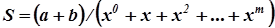
Пример 3. Перенос формулы с длинным подкоренным выражением, не умещающимся в формат набора

Формулу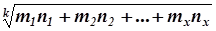

можно записать в виде    

 

 

Приложение 7. Приемы обработки формул и текста с ними, позволяющие экономить площадь бумаги

Пример 1. Перевод выражений с дробной чертой в однострочные

Формулы:                                                    

можно записать

                (aⁿ + bⁿ) / (nab);     ;  

Пример 2. Перевод выражений с дробной чертой в однострочные

Выражения:

                                                       

можно заменить

              ;                       

Пример 3. Запись с помощью ехр

Запись

                          

можно представить

 ;        

Пример 4. Свернутые формы записи обозначений

 

Сумму    а₁ + а₂ +... + а _n            можно записать в виде        ;

 

Произведение                       в виде

 

Последовательность a ₁ , a ₂ , …, a_n, …       в виде  .

 

 

Пример 5. Сокращенные формы записи матриц, определителей и систем линейных уравнений

 

Вместо матрицы

 

можно употребить краткую запись , 1≤ p ≤ n; 1≤ q ≤ n

 

 

Пример 6. Сокращенные формы записи матриц, определителей и систем линейных уравнений

Используя такую запись, можно систему уравнений

 

 

 

можно кратко записать в виде AX = B, , 1 ≤ k ≤ n; 1 ≤ l ≤ n,

                         X=(x₁ , x₂ , …, x_n), B=(b₁, b₂, …, b_n).

 

Пример 7. Замена однотипных формул, в которых величины изменяются по одному и тому же правилу, одним выражением

Текст

Формулы для первых четырех моментов имеют вид

                                  (1)

                    (2)

                  (3)

                (4)

 

         можно более компактно записать так:  

    Формулы для первых четырех моментов имеют вид

                              (h = 0; 1; 2; 3)

12345

Поделиться:

Воспользуйтесь поиском по сайту: