Модуль 2. Проецирование прямой

Начертательная геометрия.

Учебно-методическое пособие по решению задач.

 

Улан-Удэ

Издательство БГСХА им. В.Р. Филиппова

 

УДК 514.18 (075.8)

 

Печатается по решению методического совета ФГБОУ ВО «Бурятская государственная сельскохозяйственная академия им. В. Р. Филиппова»

Протокол № 8 от 3 июня 2016 г.

 

Рецензенты:

Д. Б. Лабаров – д.т.н., профессор, декан инженерного факультета ФГБОУ ВО «Бурятская государственная сельскохозяйственная академия им. В. Р. Филиппова»

Т.В. Аюшеев - д. т. н., зав. кафедрой

инженерной и компьютерной графики ВСГУТУ

 

 

Начертательная геометрия. Учебно-методическое пособие по решению задач / Б. С. Никифоров и др. – Улан-Удэ: Изд-во ФГБОУ ВО БГСХА, 2016. - 71 с.

 

 

Учебно-методическое пособие освещает основные вопросы курса начертательной геометрии в соответствии с модульной программой дисциплины для бакалавров технических специальностей вузов Задания, контрольные вопросы позволяют обучающимся усовершенствовать свои знания в теории построения чертежа и показать уровень усвоения учебного материала.

 

© Никифоров Б.С., 2016

© Хозонхонова Д.Д., 2016

© Сосоров Е.В., 2016

© Корытов Г.А., 2016

© ФГБОУ ВО «Бурятская государственная сельскохозяйственная академия им. В. Р. Филиппова», 2016

 

 

Оглавление

 

Введение. 4

Модуль 1. Метод проекций. 5

Модуль 2. Проецирование прямой. 10

Модуль 3. Проецирование плоскости. 21

Модуль 4. Способы преобразования чертежа. 35

Модуль 5. Многогранники. 51

Модуль 6. Поверхности. 60

Модуль 7. Аксонометрические проекции. 79

Задания для самостоятельной работы.. 88

Список рекомендуемой литературы.. 94

Введение

 

Начертательной геометрией называют науку, которая является теоретическим фундаментом черчения.

Начертательная геометрия занимается вопросами исследования геометрических основ построения изображений предметов на плоскости, вопросами решения пространственных геометрических задач при помощи изображений.

Изучение начертательной геометрии способствует развитию у студентов пространственных представлений и пространственного воображения - качеств, характеризующих высокий уровень инженерного мышления и необходимых для решения прикладных задач.

В процессе изучения начертательной геометрии достигаются и другие цели, расширяется общенаучный кругозор студентов, развиваются навыки логического мышления, внимательность, наблюдательность, аккуратность и другие качества, развитие которых является одной из задач обучения и воспитания в высшей технической школе.

Предметом начертательной геометрии (в узком смысле) является изучение теории построения плоских моделей пространств и теории и практики решения пространственных задач на таких плоских моделях.

В данном пособии представлены задачи для решения на практических занятиях и задания для самостоятельной работы по вариантам. Задачи разделены по уровням сложности. Задачи не обозначенные звездочкой (*) – первого уровня сложности, с одной звездочкой – второго уровня, с двумя звездочками – третий уровень.

Обозначения, принятые в пособии, представлены ниже.

1. Точки-оригиналы обозначаются прописными буквами латинского алфавита: А, В, С, …, а также цифрами: 1, 2, 3, ….

2. Линии-оригиналы обозначаются строчными буквами латинского алфавита: а, b, с, е, ….

3. Плоскости-оригиналы обозначаются прописными буквами греческого алфавита: α, β, g, ….

4. Плоскости проекций обозначаются прописной буквой греческого алфавита П с подстрочными индексами: П₁ – горизонтальная, П₂ – фронтальная, П₃ – профильная.

Новые плоскости проекций при замене плоскостей проекций обозначаются П₄, П₅,....

5. Проекции точек, линий и плоскостей обозначаются теми же буквами, что и оригиналы, только с индексами, соответствующими индексам плоскостей проекций: А₁, А₂, … L₁, L₂, L₃, ….

6. Аксонометрические проекции точек, прямых и плоскостей обозначаются буквами, соответствующими натуре, с добавлением надстрочного индекса «′»: А′, а′, Σ′, ….

7. Оси проекции: X – ось абсцисс; Y – ось ординат; Z – ось аппликат. Начало координат – прописной буквой О. Линии уровня обозначаются: h – горизонталь; f – фронталь; p – профильная прямая.

Модуль 1. Метод проекций

Вопросы для самопроверки

1) Что изучает начертательная геометрия?

2) Кого называют основателем начертательной геометрии?

3) В чем достоинства и недостатки центральных проекций?

4) В каких случаях используются центральные проекции?

5) В чем преимущества параллельных проекций?

6) Назовите свойства центрального и параллельного проецирования.

7) Сколько проекций точки определяют ее положение относительно плоскостей проекций?

8) Что называется эпюром Монжа?

9) Как называются и обозначаются плоскости проекций?

10) Назовите название ортогональных проекции точек на плоскости проекций П₁ и П₂.

11) Что значит спроецировать точку на две или три взаимно перпендикулярные плоскости проекций?

12) Каков алгоритм построения 3-й проекции точки?

Примеры решения задач

Пример 1

Построить комплексные чертеж точки: А (15,30,0),

x_A = 15 мм; y_A = 30мм; z_A = 0.

Рисунок 1

Решение. Если у точки одна координата равна нулю, то точка принадлежит одной из плоскостей проекции. В данном случае у точки нет высоты: z = 0, следовательно точка А лежит в плоскости П₁.

На комплексном чертеже оригинал (т.е. сама точка А) не изображается, есть только ее проекции.

Пример 2

Определить местоположение точек A, B, C, D в пространстве (рис. 2).

Рисунок 2

Решение. Заданные на рис. 2 точки расположены следующим образом в пространстве:

- точка А лежит на фронтальной плоскости проекций, так как координата y_А точки А равна 0;

- точка В расположена на профильной плоскости (x_B=0);

- точка С расположена в 1 четверти пространства (все координаты положительны);

- точка D лежит в горизонтальной плоскости (z_D=0).

 

Пример 3

Дана точка А (10, 12, 20). Построить эпюр точки В, симметричной точке А относительно: горизонтальной плоскости проекций (рис. 3, а), вертикальной плоскости проекций (рис. 3, б), оси проекций (рис. 3, в).

Решение. Точка (А₁, А₂) задана в первой четверти.

1. Точка, симметричная ей относительно горизонтальной плоскости проекций, находится в четвертой четверти, т. е. В (10, 12, —20). Построив эпюр точки (А₁, А₂), откладываем на общем перпендикуляре вниз отрезки А_xB₁ длиной 12 мм (у) и А_xB₂ длиной 20 мм (z).

а) б) в)

Рисунок 3

 

 

2. Точка, симметричная ей относительно вертикальной плоскости проекций, находится во второй четверти, т. е. В (10, -12, 20). Построив, как и прежде, эпюр точки (А₁, А₂), откладываем на общем перпендикуляре вверх отрезки А_xB₁ длиной 12 мм (у) и А_xB₂ длиной 20 мм (z).

3. Точка, симметричная ей относительно оси проекций, находится в третьей четверти, т. е. В (10, —12, —20). Построив, как и прежде, эпюр точки (А₁, А₂), откладываем на общем перпендикуляре: вверх отрезок А_xB₁ длиной 12 мм (у) и вниз отрезок А_xB₂ длиной 20 мм (z).

Задачи по модулю 1

1. Построить проекции точки А, находящейся в первой четверти пространства, во второй, в третьей, в четвертой четверги пространства (рис. 4 а-г).

 

2. Построить проекции точки А при условии z= 0 (рис. 4 а, в), при условии у = 0 (рис. 4 б, г).

а) б)     в) г) Рисунок 4

3. Построить эпюр точки заданных координатами:

	А	B	C	D	E	F	G
x
y				-25	-20		-30
z		-40	-25	-15

 

4*. Построить эпюр точек A, B, C, находящихся в указанной четверти, если дана одна из ее проекций и зависимость между координатами (у= z + n) (рис. 5,а-в).

Исходные данные задачи:

для точки А

1четв. n=15

для точки B

4 четв. n=20

для точки C

2 четв. n=10

 

а) б) в)

Рисунок 5

а) б) в)

Рисунок 6

5*. Построить эпюр точки E, F, G, H, находящихся в указанной четверти, если дана одна из ее проекций и отношение расстояний oт этой точки до плоскостей проекций (у = m) (рис. 6, а-г).

Исходные данные задачи:

для точки E

1 четв. m=2

для точки F

4 четв. m=1.5

для точки G

2 четв. m=1

 

6**. Построить эпюр точки В, симметричной точке А(10,-25,30), относи­тельно горизонтальной плоскости проекций, фронтальной плоскости про­екций, oси проекций.

 

7**. Даны точка А и фронтальная проекция точки В. В какой четверти находится точка В, если расстояние между их горизонтальными проекциями равно 25 мм (рис. 7)?

Рисунок 7

Модуль 2. Проецирование прямой

Вопросы для самопроверки

1) Как задать на эпюре прямую линию?

2) Как определяется расстояние от точки до плоскостей проекций П1, П2, П3?

3) Может ли проекция прямой линии представлять собой точку?

Перечислите прямые частного положения?

4) Какими методами на эпюре определяется натуральная величина и углы наклона отрезка прямой общего положения к плоскостям проекций?

5) Что называется следом прямой линии?

6) Как на эпюре расположены проекции пересекающихся прямых?

7) Каким способом на эпюре определяют натуральную величину отрезка прямой общего положения и углы наклона его к плоскостям проекций?

 

Примеры решения задач

Пример 4

Найти на прямой АВ точку С, зная отношение ее координат: (рис. 8).

Рисунок 8

Решение. Координаты z и у определяют профильную проекцию (C₃) точки С. Геометрическое место точек плоскости в системе ZOY с отношением координат есть прямая линия, уравнение которой у = 2z. Профильная проекция (C₃) у точки С должна лежать на профильной проекции (A₃B₃) заданной прямой АВ и на прямой у = 2z, т. е. на их пересечении. Следовательно, по заданным проекциям прямой АВ находим ее профильную проекцию (A₃B₃), проводим в системе ZOY прямую у = 2z и на их пересечении получаем профильную проекцию (C₃) точки С.

Затем уже по C₃ находим горизонтальную и вертикальную проекции искомой точки на одноименных проекциях прямой АВ.

Пример 5

Параллельные прямые АВ и CD пересечь произвольной прямой (рис.9).

Рисунок 9

Решение. Берем на каждой из заданных прямых АВ и CD по произвольной точке. Прямая, проведенная через эти две точки, будет искомой. Отсюда — задаем произвольную точку (M₁, M₂) на прямой АВ и точку (N₁,N₂) на прямой CD. Затем проводим горизонтальную проекцию искомой прямой через точки M₁ и N₁ и фронтальную проекцию M₂ и N₂.

Эту задачу можно решить несколько иначе. Пересекаем вертикальные проекции произвольной прямой и отмечаем точки пересечения M₂ и N₂. По точке M₂ находим M₁ на горизонтальной проекции прямой АВ и по точке N₂ находим N₁ на горизон­тальной проекции прямой CD. Проводим через полученные точки M₁ и N₁ горизон­тальную проекцию искомой прямой. Можно было бы начать решение задачи также с проведения произвольно горизонтальной проекции искомой прямой, а затем поступить так же, как и выше.

Пример 6

Прямые АВ и CD пересечь прямой, параллельной горизонтальной плоскости проекций (рис. 10).

Решение. Искомая прямая должна быть параллельна горизонтальной плоскости проекций, а следовательно, ее фронтальная проекция должна быть параллельна оси ОХ. Отсюда — проводим произвольно фронтальную проекцию искомой прямой параллельно оси проекций; точки пересечения с прямыми A₂B₂ и C₂D₂ обозначаем через K₂ и M₂. По точкам K₂ и M₂ находим на прямых A₁B₁ и C₁D₁ точки K₁ и M₁. Проводим через точки K₁ и M₁ горизонтальную проекцию (K₁ M₁) искомой прямой.

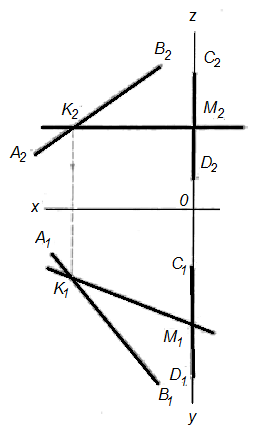
Рисунок 10

Пример 7

Построить проекции прямой зная ее следы (рис. 11).

Решение. Искомая прямая проходит через следы – точки N₀ и M₀. Следовательно, проекции прямой должны пройти через одноименные проекции этих точек. Находим проекции (N₁, N₂) и (M₁, M₂) этих точек и проводим горизонтальную проекцию прямой через точки N₁ и M₁, фронтальную проекцию прямой – через точки N₂ и M₂.

Пример 8

Найти следы прямой АВ и отделить видимую ее часть от невидимой (рис. 12)

Решение. Продолжаем горизонтальную проекцию (А₁В₁) прямой до пересечения с осью х в точке N₁. В этой точке восставляем перпендикуляр к оси проекций до пересечения с фронтальной проекцией прямой (А₂В₂) в точке N₂. Получаем фронтальный след прямой.

 

Рисунок 11

 

Рисунок 12

Затем продолжаем фронтальную проекцию прямой до пересечения с осью проекций х в точке М₂. В этой точке восставляем перпендикуляр к оси проекций до пересечения с горизонтальной проекцией прямой в точке M₁. Получаем горизонтальный след прямой.

Прямая проходит через первую, вторую и третью четверти пространства.

Пример 9

Определить действительную длину отрезка АВ (рис. 13).

Рисунок 13

Решение. Строим прямоугольный треугольник по двум катетам. За один катет принимаем горизонтальную проекцию (A₁B₁) отрезка, а за другой катет - отрезок, длина которого равна |z + z₁|. Гипотенуза этого прямоугольного треугольника дает нам действительную длину отрезка.

Тот же результат получаем, построив прямоугольный треугольник, одним катетом которого является фронтальной проекция (А₂В₂) отрезка, а другим катетом - отрезок длиной |y₁—у|. Гипотенуза этого треугольника дает нам действительную длину отрезка.

В обоих случаях получается один и тот же результат.

Пример 10

Отложить на прямой АВ от точки К отрезок длиной 28 мм по направлению от точки А к точке В (рис. 14).

Решение. Выделяем на прямой АВ (условно) произвольный отрезок КМ и определяем его действительную величину. Для этого строим прямоугольный треугольник по двум катетам (К₂М₂) и | у — y₁|. Откладываем на гипотенузе построенного треугольника отрезок КС длиной 28 мм и опускаем из точки С перпендикуляр на прямую А₂В₂ до пересечения с ней в точке С₂. По точке С₂ находим точку С₁ на прямой А₁В₁. Проекциями искомого отрезка являются (К₁С₁, К₂С₂).

Рисунок 14

Рисунок 15

Пример 11

Определить углы наклона прямой АВ к плоскостям проекций (рис. 15).

Решение. Строим, как было указано, прямоугольные треугольники A₁B₁B* и A₂B₂A*. Угол α является углом наклона данной прямой к горизонтальной плоскости проекций; угол β является углом наклона той же прямой к фронтальной плоскости проекций.

Задачи по модулю 2

1. Найти на прямой АВ точку С, если расстояние от фронтальной плоскости проекций z=20 (рис. 16).

Рисунок 16

2. Найти на прямой АВ точку К с соотношением координат (рис. 16).

 

3. Проставить пропущенные слова.

А) Отрезок АВ лежит на (?) плоскости проекций (рис. 17,а).

Б) Отрезок АВ находится в (?) четверти, расположен параллельно (?) плоскости проекций и концом А упирается в (?) плоскость проекций (рис. 17,б).

В) Отрезок АВ находится в (?) четверти, расположен перпендикулярно (?) плоскости проекций и концом А упирается в (?) плоскость проекций (рис. 17,в).

Г) Отрезок АВ находится в (?) четверти и расположен параллельно (?) плоскости проекций (рис. 17,г).

 

4*. Построить эпюр отрезка АВ если он:

а) общего положения, находится во второй четверти и упирается концом А в фронтальную плоскость проекций;

б) находится в первой четверти, расположен параллельно вертикальной плоскости проекций и упирается концом А в плоскость проекций;

а) б)

в) г)

Рисунок 17

в) лежит произвольно на горизонтальной плоскости проекций в первой четверти;

г) находится в четвертой четверти, расположен перпендикулярно горизонтальной плоскости проекций, и его конец А одинаково удален от плоскостей проекций;

д) находится в третьей четверти, расположен параллельно горизонтальной плоскости проекций и его конец А упирается в плоскость проекций;

е) находится в плоскости биссектора первой четверти и параллелен оси проекций;

ж) находится в четвертой четверти, расположен параллельно фронтальной плоскости проекций и его конец А одинаково удален от плоскостей проекций;

з) общего положения, находится в третьей четверти, упирается концом А в горизонтальную плоскость проекций и его конец В одинаково удален от плоскостей проекций;

и) лежит на верхней поле вертикальной плоскости проекций и параллелен оси проекций;

к) находится во второй четверти, упирается концом А в ось проекций и его конец В одинаково удален от плоскостей проекций;

л) находится в третьей четверти, расположен перпендикулярно вертикальной плоскости проекций и упирается концом В в плоскость проекций.

 

5. Определить взаимное расположение прямых АВ н CD (рис.18, а-в)

 

6. Найти следы прямой АВ на рис. 16.

 

7*. Найти следы прямых АВ и DС на рис. 18, в.

а) б) в)

Рисунок 18

8*. Дана точка А (20, 30, 20). Построить эпюр точки В, симметричной точке А, относительно осей OX, OY, OZ (дать три эпюра).

 

9**. Построить проекции куба с основанием ABCD на вертикальной плоскости проекций, если дана диагональ АС его основания, и указать проекции каждой грани, каждого ребра (рис. 19, а).

 

10**. Построить проекции правильной треугольной прямой призмы высотой 50 мм, если дана сторона АВ ее основания, лежащего на горизонтальной плоскости проекций, указать проекции каждой грани, каждого ребра (рис. 19, б).

а) б)

Рисунок 19

11**. Построить проекции прямой правильной треугольной пирамиды высотой 60 мм, если дана сторона АВ ее основания, лежащего на вертикальной плоскости проекций, и указать проекции каждой грани, каждого ребра (рис. 19).

Рисунок 20

12**. Построить проекции прямого кругового цилиндра с основанием на вертикальной плоскости проекций и с центром С (30, 0, 30), если дана его высота 60 мм, а радиус основания равен 20 мм.

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: