Модуль 4. Способы преобразования чертежа

Вопросы для самопроверки

1) Для чего нужны способы преобразования ортогональных проекций?

2) В чем сущность способа замены плоскостей проекций?

3) Сформулируйте алгоритм построения новой проекции точки при замене плоскости проекций.

4) Каким образом получаются проекции при помощи метода вращения?

5) В чем сущность способа плоскопараллельного перемещения.

6) Составьте алгоритм решения задачи на преобразование прямой общего положения в прямую уровня, проецирующую прямую.

7) Опишите алгоритм решения задачи на преобразование плоскости общего положения в плоскость проецирующую, а затем в плоскость уровня.

Примеры решения задач

Пример 24

Повернуть точку А вокруг оси I, перпендикулярной к плоскости П₁, на угол 120° по направлению движения часовой стрелки (рис. 40, а).

Решение: Точка А при ее вращении вокруг оси I описывает в плоскости R, перпендикулярной к оси вращения, т. е. в плоскости, параллельной плоскости Н, окружность радиуса А₁I₁. Горизонтальная проекция (A₁) точки описывает дугу A₁A'₁ окружности радиуса А₁I₁ с центральным углом α= 120°. Фронтальная проекция A_2­ точки движется по прямой, параллельной оси проекций (z = const). Зная новое положение горизонтальной проекции (A₁) точки, находим ее фронтальную проекцию A'₂.

а) б)

Рисунок 40

 

Пример 25

Повернуть точку А вокруг оси I, перпендикулярной к плоскости П₂, на угол 120° по направлению движения часовой стрелки (рис. 40, б).

Решение: Точка Aпри ее вращении вокруг оси I описывает в пло­скости R, перпендикулярной к оси вращения, т. е. в плоскости, параллельной плоскости П₂, окружность радиуса А₂I₂. Фронтальная проекция (А₂) точки описывает дугу A₂A'₂ окружности радиуса А₂I₂ с центральным углом α = 120°. Горизонтальная проекция (А₁) точки движется по прямой, параллельной оси проекции (у = const). Зная новое положение фронтальной проекции (A₂) точки, находим ее горизонталь­ную проекцию (A'₁).

Пример 26

Отрезок АВ привести в положение, параллельное горизонтальной плоскости проекций методом плоскопараллельного перемещения (рис. 41).

Решение. Перемещаем отрезок параллельно фронтальной плоскости проекции. Так как отрезок должен находиться в положении, параллельном горизонтальной плоскости проекции, его фронтальная проекция должна быть параллельна оси проекций. Задаем над осью проекций отрезок A'₂B'₂ в положении, параллельном оси проекций, равный отрезку A₂B₂ и затем по фронтальной проекции (A'₂B'₂) отрезка находим его горизонтальную проекцию (A'₁ B'₁).

Рисунок 41

Пример 27

Отрезок АВ привести в положение, перпендикулярное к горизонтальной плоскости проекций методом плоскопараллельного перемещения (рис. 42).

Решение. Так как отрезок AВ задан в положении, параллельном фронтальной плоскости проекции, то достаточно одного его перемещения параллельно фронтальной плоскости проекций. Задаем отрезок A₂'B₂'в положении, перпендикулярном к оси проекций (почему?), равный отрезку A₂B₂, н затем по фронтальной проекции (A₂'B₂') отрезка находим его горизонтальную проекцию (A₁B₁) в виде точки.

Рисунок 42

Пример 28

Определить угол между пересекающимися прямыми (АВ и ВС) методом плоскопараллельного перемещения.

Решение: 1) построим горизонтальную проекцию угла в свободном месте чертежа таким образом, чтобы проекция A₁B₁ была перпендикулярна к оси х (рис. 43). Таким образом получили новое положение горизонтальной проекции угла (А'₁B'₁C'₁).

2) по линиям связи от фронтальной проекции A₂B₂C₂ воспроизвели новое положение фронтальной проекции угла (A'₂B'₂C'₂) (в точности получился отрезок А'₂C'₂)

3) получившийся отрезок перечерчиваем на новом месте чертежа так, чтобы он располагался горизонтально. Получаем новое положение фронтальной проекции (А''₂B''₂C''₂).

4) по линиям связи от фронтальной проекции А''₂B''₂C''₂ воспроизвели новое положение фронтальной проекции угла (А''₂B''₂C''₂).

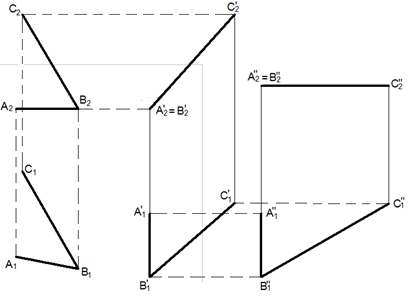
Рисунок 43

Пример 29

Найти центр круга, описанного около треугольника АБС с использованием метода плоскопараллельно перемещения (рис. 44).

Решение. Центр круга, описанного около треугольника, находится па пересечении перпендикуляров, проведенных к его сторонам через их середины. Для того чтобы можно было провести эти перпендикуляры, нужна натуральная величина треугольника, для чего необходимо привести плоскость треугольника в положение, параллельное одной из плоскостей проекций, например плоскости П₁. Такого положения достигаем, выполнив два последовательных перемещения: первое - перпендикулярно фронтальной плоскости проекций и второе - параллельно горизонтальной плоскости проекций.

 

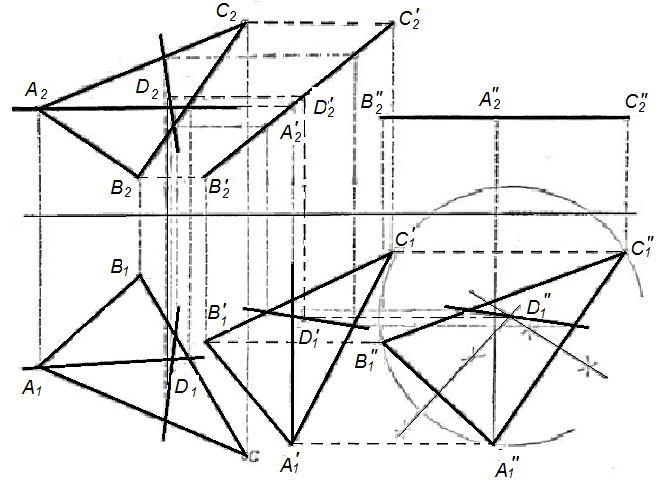
Рисунок 44

 

Пример 30

Пересечь прямые АВ и CD перпендикулярной к ним прямой MN с использованием плоскопараллельного перемещения (рис. 45).

Решение. Перемещаем прямые (A₁B₁, A₂B₂) и (C₁D₁) так, чтобы одна из прямых, например (A₁B₁, A₂B₂), заняла положение, перпендикулярное к горизонтальной плоскости проекций.

Так как прямая (A₁B₁, A₂B₂) — общего положения, следует, как известно, произвести два последовательных перемещения заданной системы: первое — параллельно плоскости П₂, при котором прямая (A'₁B'₁, A'₂B'₂) параллельна фронтальной плоскости проекций, и второе — параллельно фронтальной плоскости проекций, при котором прямая (A"₁B"₁, A"₂B"₂) перпендикулярна горизонтальной плоскости проекций. Пересекаем прямые (A"₁B"₁, A"₂B"₂) и (С"₁D"₁, C"₂D"₂) перпендикулярной прямой (M"₁N"₁, M"₂N"₂), а затем находим прямую (M₁N₁, M₂N₂) в первоначальном задании. Построение видно из чертежа.

Рисунок 45

 

Пример 31

Построить линию пересечения пирамиды плоскостью Р (рис. 46).

Решение. Для построения линии пересечения нужно найти точки пересече­ния боковых ребер пирамиды с плоскостью; так как и ребра пирамиды и сама плоскость Р — общего положения, целесообразно изменить положение заданной системы так, чтобы плоскость Р стала фронтально-проецирующей.

Проводим горизонталь плоскости и, перемещая систему параллельно горизонтальной плоско­сти проекций, приводим горизонталь в положение, перпендикулярное к плоскости П₂, а плоскость P — в положение, перпендикулярное к плоскости П₂. Построив элементы заданной системы, после перемещения находим по известному правилу проекции А₂'B₂'C₂'D₂') линии пересечения пирамиды плоскостью P; затем находим проекции линии пересечения в первоначальном задании. Построе­ние видно из чертежа.

Рисунок 46

 

Пример 32

Совместить плоскость Р с горизонтальной плоскостью проекций (рис. 47).

Решение. Вращаем плоскость Р вокруг горизонтального следа (P₁) плоскости. Чтобы найти совмещенный фронтальный след (Р₂) плоскости, задаем на следе Р₂ произвольную точку (V₁, V₂) и находим ее совмещенное положение V₀ на плоскости P (построение видно из чертежа). Проводим через точки Р_х и V₀ искомый совмещенный фронтальный след (Р₂) плоскости.

Угол j— истинный угол между следами плоскости.

Из чертежа видно, что P_XV₀ = P_xV₂. Пользуясь этим, можно упростить решение задачи. Опускаем из точки V перпендикуляр на след P₁ и из точки Р_х радиусом, равным P_x описываем дугу до пересечения с перпендикуляром в точке V₀. Проводим совмещенный след Р₁ через точки Р_х и V₀.

Рисунок 47

 

Пример 33

Построить проекции окружности, лежащей в плоскости Р, если даны ее центр С и радиус 20 мм (рис.48).

Решение. Окружность проецируется на плоскости проекций эллипсами, причем большая ось эллипса всегда равна диаметру окружности. Так как окружность лежит в плоскости общего положения, то невозможно выделить тот ее диаметр, который на обе плоскости проецируется без искажения.

Рисунок 48

 

Следовательно, главные оси эллипсов на горизонтальной плоскости проекций и на фронтальной плоскости проекций следует находить независимо одну от другой. На горизонтальную плоскость проекций без искажения проецируется в большую ось тот диаметр окружности, который расположен на горизонтали плоскости; диаметр, перпендикулярный к этому диаметру, проецируется с искажением в малую ось перпендикулярно (на основании теоремы проектирования прямого угла) большой оси. Аналогично на фронтальную плоскость проекций без искажения проецируется в большую ось эллипса тот диаметр окружности, который расположен на фронтали плоскости; диаметр, перпендикулярный к этому диаметру, проецируется с искажением в малую ось эллипса перпендикулярно большой его оси. Отсюда ход построений таков:

1) совмещаем заданную плоскость, например с горизонтальной плоскостью проекций, и находим положение точки С₀ — центра окружности;

2) описываем из точки С₀ окружность заданного радиуса и проводим две пары взаимно перпендикулярных диаметров — диаметр, параллельный следу Р₁ и ему перпендикулярный, и диаметр, параллельный следу P₂' и ему перпендикулярный; затем находим горизонтальные проекции первой пары диаметров окружности и фронтальные проекции второй пары диаметров.

Дальнейшее построение видно из чертежа.

Выводы:

1. Главными осями эллипса на горизонтальной плоскости проекций являются горизонтальные проекции двух взаимно перпендикулярных диаметров, из которых один расположен параллельно горизонтальной плоскости проекций.

2. Главными осями эллипса на фронтальной плоскости проекций являются фронтальные проекции двух взаимно перпендикулярных диаметров, из которых один расположен параллельно фронтальной плоскости проекций.

 

Пример 34

Дан отрезок АВ.Найти его проекции, если в новой системе он должен быть расположен параллельно фронтальной плоскости проекций (рис. 49,а).

Решение. Для того чтобы отрезок был параллелен фронтальной плоскости проекций нужно, чтобы горизонтальная его проекция была параллельна оси про­екций. Проводим ось проекций, параллельно горизонтальной проекции отрезка (А₁В₁). Проводим перпендикуляр через точку А₁ к построенной оси, и откладываем на нем отрезок от оси, равный координате z точки А. Таким образом получаем фронтальные проекции точек (А₂' и В₁') в новой системе.

а) б)

Рисунок 49

Пример 35

Дан отрезок АВ. Найти его проекции, если в новой системе он должен быть расположен перпендикулярно горизонтальной плоскости проекций (рис. 49,б).

Решение. Для того чтобы отрезок был перпендикулярен горизонтальной плоскости проекции, нужно, чтобы его фронтальная проекция была перпендикулярна оси проекций. Проводим ось проекций перпендикулярно фронтальной проекции (А₂В₂) отрезка и, как было указано, находим его горизонтальную проекцию (А₃В₃) в виде точки.

Пример 36

Определить расстояние от точки М до прямой а с применением метода замены плоскостей рис. 50, а.

Решение: 1) Фиксируем систему П₁ /П₂ проводим ось Х через одну из точек отрезка прямой (точка 2) (рис.50, б).

 

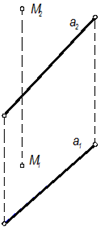
а) б)

Рисунок 50

2) Введем дополнительную плоскость проекций П₄, причем П₄ перпендикулярна П₁, П₄ параллельна a (построим ось x₁ параллельно a₁).

Прямая а (а₄) - заняла положение прямой уровня в системе П₁ – П₄, при этом расстояние КМ будет перпендикулярно а (К₄М₄ перпендикулярна а₄). Измерив отрезок К₄М₄ узнаем натуральную величину расстояния от точки М до прямой а.

 

Пример 37

Найти центр окружности, описанной около треугольника ABC (рис. 51).

Решение. Центр окружности, описанной около треугольника, находится на пересечении перпендикуляров, проведенных к его сторонам через их середины.

Для того чтобы провести эти перпендикуляры, нужно иметь натуральную величину треугольника, а для этого необходимо, чтобы одна из плоскостей проекций, например горизонтальная, была параллельна плоскости треугольника.

Рисунок 51

Пользуемся последовательно двумя переменами плоскостей проекций. Сначала заменяем фронтальную плоскость проекций новой (П₃), которая перпендикулярна плоскости треугольника, а затем заменяем горизонтальную плоскость проекций новой (П₄), которая параллельна плоскости треугольника.

Проводим горизонталь ВК треугольника и, задавшись осью П₁/П₃ проекций, перпендикулярной (почему?) к горизонтальной проекции (В₁ К₁) горизонтали, находим новую фронтальную проекцию (А₃В₃С₃) треугольника в виде прямой. Затем проводим ось П₃/П₄ проекций параллельно (почему?) новой фронтальной проекции (А₃В₃С₃) треугольника и находим его новую горизонтальную проекцию (А₄В₄С₄).

Треугольник А₄В₄С₄ — натуральная величина заданного треугольника ABC. Найдя центр (D₄) окружности, описанной около треугольника А₄В₄С₄, находим проекции (D₁, D₂) этой точки в первоначальном задании (построение видно из чертежа).

Задачи по модулю

1. Прямую АВ поставить в положение, параллельное горизонтальной плоскости проекций. (рис. 52, а, б)

 

2. Прямую АВ поставить в положение, параллельное фронтальной плоскости проекций. (рис. 52, а, б)

 

3. Прямую АВ поставить в положение, перпендикулярное к горизонтальной плоскости проекций. (рис. 52, в, г)

 

 

а) б)   в) г) Рисунок 52

4*. Треугольник АВС поставить в такое положение, чтобы его горизонтальная проекция сливалась в прямую линию (рис. 53).

Рисунок 53

5*. Построить окружность, описанную около треугольника АВС, лежащего в плоскости Р (рис. 54).

Рисунок 54

6**. Пересечь прямые АВ и CD прямой МN, перпендикулярной к прямой АВ, так, чтобы отрезок прямой МN между заданными прямыми имел длину, равную 20 мм. (рис. 55)

Рисунок 55

Модуль 5. Многогранники

Вопросы для самопроверки

1) Что называется многогранником?

2) Какой многогранник называется правильным?

3) Назовите виды многогранников.

4) Какой многогранник называется призмой?

5) Какой многогранник называется пирамидой?

6) Способы построения фигуры сечения многогранника плоскостью.

7) Каков порядок построения линии взаимного пересечения многогранников?

Примеры решения задач

Пример 38

Найти линию пересечения поверхности призмы с плоскостью Р (рис. 56).

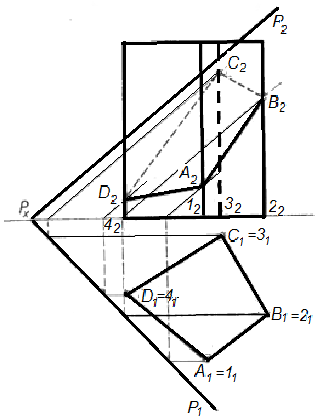
Рисунок 56

Решение. Для того, чтобы построить линию пересечения, нужно найти точки пересечения ребер призмы с данной плоскостью.

Находим точку (А₁, А₂) пересечения ребра (1₁, 1₂) с плоскостью Р. Горизонтальная проекция (А₁) этой точки совпадает с горизонтальной проекцией ребра; зная это, находим фронтальную проекцию (А₂) точки, пользуясь условием, что точка (А₁, А₂) лежит и на плоскости Р, используя фронталь плоскости, проходящую через точку А (см. построение рис. 56).

Аналогичным порядком находим точки (В₁, В₂), (С₁,С₂) и (D₁, D₂) пересечений остальных ребер с плоскостью Р.

Соединив последовательно найденные точки, получаем проекции искомой линии пересечения: горизонтальную (А₁В₁С₁D₁) и фронтальную (А₂В₂С₂D₂). Из чертежа видно, что горизонтальная проекция (А₁В₁С₁D₁) линии пересечения совпадает с горизонтальной проекцией (1₁2₁3₁4₁) призмы.

Пример 39

Найти линию пересечения поверхности призмы с плоскостью Р (рис. 57).

Рисунок 57

Решение. Нужно найти точки пересечения ребер призмы с плоскостью Р. Находим точку (А₁, А₂) пересечения ребра (1₁,1₂) с плоскостью: заключаем ребро в плоскость R, параллельную фронтальной плоскости проекций, которая пересекает плоскость Р по фронтали. На пересечении фронтальных проекций ребра и фронтали получаем фронтальную проекцию (А₂) точки; зная ее, находим горизонтальную проекцию (А₁) точки па горизонтальной проекции ребра. Аналогичным образом находим точки (B₁, B₂), (C₁, C₂) и (D₁, D₂) пересечений остальных ребер с плоскостью.

Соединив последовательно найденные точки, получаем проекции искомой линии: горизонтальную (А₁В₁С₁D₁) и фронтальную (А₁В₁С₁D₁).

 

Пример 40

Найти линию пересечения поверхности пирамиды с плоскостью Р (рис. 58).

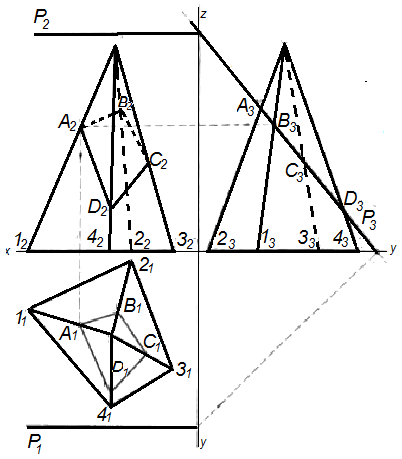
Рисунок 58

Решение. Находим точки пересечений боковых ребер пирамиды с профильно-проецирующей плоскостью. Строим профильную проекцию пирамиды и профильный след (Р₃) плоскости. На пересечении профильных проекций ребер пирамиды со следом Р₃ получаем профильные проекции точек пересечений ребер с плоскостью; зная их, находим горизонтальные и фронтальные проекции этих точек.

Соединив последовательно найденные точки, получаем проекции искомой линии пересечения: горизонтальную (А₁В₁С₁D₁) и фронтальную (А₂В₂С₂D₂). Решение задачи без профильной плоскости проекции усложнило бы построение (почему?).

Пример 41

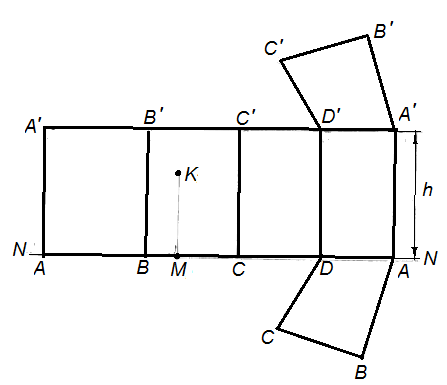
Дать полную развертку поверхности четырехугольной призмы (рис. 59).

Решение. Полная поверхность заданной призмы состоит из четырех прямоугольников и двух четырехугольников.

Проводим произвольную прямую NN и на ней от точки А откладываем отрезки АВ, ВС, CD, DA, равные сторонам основания призмы, т. е. АВ = А₁В₁, ВС = В₁С₁ и т. д. Через точки А, В, С, D, А проводим перпендикуляры к прямой NN и на них откладываем одинаковые (почему?) отрезки длиной h соединив концы перпендикуляров, получаем прямую А'B'C'D'A', параллельную прямой ABCDA. Затем пристраиваем, например, при стороне AD, нижнее основание призмы, а при стороне — верхнее ее основание.

Пример 42

Найти точки пересечения поверхности призмы с прямой АВ (рис. 60).

Решение. Заключаем прямую АВ в фронтально- или горизонтально-проецирующую плоскость R, которая пересекает поверхность призмы по четырехугольнику.

 

а)

б)

Рисунок 59

Рисунок 60

На пересечении горизонтальных проекции полученного четырехугольника и заданной прямой находим горизонтальные проекции (M₁) и (N₁) искомых точек; зная их, находим фронтальные проекции (M₂) и (N₂) точек на прямой A₂B₂. В данном случае искомые точки можно найти и не вводя плоскость R (почему?).

Пример 43

Найти точки пересечения поверхности пирамиды с прямой АВ (рис. 61).

Решение. Заключаем прямую АВ в горизонтально-проецирующую плоскость R, которая пересекает поверхность пирамиды по четырехугольнику. На пересечении фронтальных проекций полученного четырехугольника и заданной прямой находим фронтальные проекции (M₂) и (N₂) искомых точек; зная их, находим горизонтальные проекции (M₁) и (N₁) точек на прямой A₁B₁.

Рисунок 61

Задачи по модулю 5

1. Найти точки пересечения многогранника с прямой линией (рис. 62, а,б).

а) б)

Рисунок 62

2*. Пересечь многогранник плоскостью Р и дать полную развертку одной из его частей (рис. 63-65).

а) б)

Рисунок 63

а) б)

Рисунок 64

а) б)

Рисунок 65

Модуль 6. Поверхности

Вопросы для самопроверки

1) Что такое поверхность?

2) Что такое образующая (или производящая) линия поверхности?

3) Что такое направляющая линия?

4) В чём разница между линейчатой и нелинейчатой поверхностями?

5) Как образуются цилиндрическая и коническая поверхности?

6) Что называется поверхностью вращения?

7) Что называется параллелями и меридианами на поверхности вращения, экватором, горлом, главным меридианом?

8) В чём заключается общий приём построения кривой линии, получающейся при пересечении цилиндрической и конической поверхностей плоскостью?

9) Какие линии получаются при пересечении цилиндра вращения плоскостью?

10) Какие линии получаются при пересечении конуса вращения плоскостью?

11) В чём суть способа параллельно-секущих плоскостей? В каких случаях применяются вспомогательные секущие плоскости, параллельные какой-либо плоскости проекций, для построения линии взаимного пересечения поверхностей?

12) В чём суть способа секущих сфер? Условия применимости способа концентрических сфер к построению взаимного пересечения поверхностей.

Примеры решения задач

Пример 44

Задать на поверхности наклонного цилиндра произвольную точку А (рис. 66, а).

Решение. Задаем произвольную точку (M₁, M₂) на основании цилиндра и проводим через нее вспомогательную образующую. На этой образующей берем точку (A₁, A₂), которая и лежит на заданной поверхности.

а) б)

Рисунок 66

Пример 45

Найти фронтальную, проекцию точки А, лежащей на поверхности наклонного цилиндра, если дана ее горизонтальная проекция (рис. 66, б).

Решение. Проводим через точку A горизонтальную проекцию (A₁M₁) вспомогательной образующей. Находим фронтальную проекцию (M₂) точки М и проводим через нее фронтальную проекцию образующей; затем на ней по точке А₁ с помощью линий связи находим точку А₂.

Пример 46

Задать на поверхности конуса произвольную точку А.

Решение. Первый способ (рис. 67, а). Задаем произвольную точку (М₁, М₂) на основании конуса и проводим вспомогательную образующую через точки (М₁, М₂) и (S₁, S₂). На этой образующей берем точку (A₁, A₂), которая и лежит на заданной поверхности.

Второй способ (рис. 67, б). Проводим на поверхности конуса вспомогательную окружность; ее фронтальная проекция является прямой линией, параллельной оси проекций, а ее горизонтальная проекция — окружностью. На этой окружности берем точку (A₁, A₂), которая и лежит на заданной поверхности.

а) б)

Рисунок 67

Пример 47

Построить проекции линии пересечения плоскости Р с поверхностью цилиндра (рис. 68).

Решение. Проводим через ось цилиндра горизонтально-проецирующую плоскость R, перпендикулярную к плоскости Р; плоскость R пересекает поверхность цилиндра по образующим, а плоскость Р — по прямой (H₁V₁, H₂V₂); на их пересечении получаем низшую точку (N₁, N₂) и высшую точку (M₁, M₂) лилии пересечения. Проводим через ось цилиндра плоскость R' параллельную фронтальной плоскости проекций; плоскость R' пересекает поверхность цилиндра по крайним образующим, а плоскость Р — по фронтали; на их пересечении получаем точки (А₁, А₂) и (В₁, В₂) линии пересечения.

Находим точки пересечения профильных образующих цилиндра с плоскостью Р. Горизонтальные проекции (С₁) и (D₁) этих точек известны (почему?); по ним, пользуясь горизонталями, находим фронтальные проекции (C₂) и (C₂). Аналогично находим точки пересечения еще нескольких образующих цилиндра с плоскостью. Соединив последовательно фронтальные проекции всех найденных точек, получаем фронтальную проекцию линии пересечения - эллипс. Истинную величину эллипса можно построить по главным осям; большая ось равна длине отрезка (M₁N₁, M₂N₂), а малая ось — диаметру цилиндра.

 

 

Рисунок 68

Пример 48

Построить проекции линии пересечения плоскости Р с поверхностью конуса (рис. 69).

Решение. Плоскость Р пересекает поверхность конуса по эллипсу, фронтальная проекция которого совпадает с фронтальным следом (Р₂) плоскости. Горизонтальную проекцию эллипса строим по точкам: задаем фронтальные проекции ряда его точек и находим их горизонтальные проекции. Затем через горизонтальные проекции точек проводим плавную кривую-эллипс.

Горизонтальную проекцию линии пересечения, как эллипс, можно построить также по главным осям: по большой оси АВ и по малой оси CD. Истинную величину эллипса можно построить по двум его главным осям: по большой оси A₂B₂ и по малой оси C₁D₁, которую находим по фронтальной проекции (C₂D₂).

Рисунок 69

Пример 49

Построить проекции линии пересечения плоскости Р с поверхностью шара (рис. 70).

Решение. Плоскость Р пересекает поверхность шара по окружности, горизонтальная проекция (С₁D₁) которой совпадает с горизонтальным следом (Р.) плоскости. Фронтальную проекцию окружности - эллипс строим по главным его осям: большой осью является фронтальная проекция (А₂В₂ ) диаметра, расположенного перпендикулярно горизонтальной плоскости проекций, а малой осью – фронтальная проекция (С₂D₂) диаметра, расположенного параллельно горизонтальной плоскости проекций. Фронтальную проекцию окружности можно построить также по точкам; задаем горизонтальные проекции ряда точек окружности и находим их фронтальные проекции. Затем полученные точки соединяем плавной кривой – эллипсом.

 

Рисунок 70

 

Для того чтобы отделить на горизонтальной проекции кривой видимую ее часть от невидимой, находим фронтальной проекции (М₂) и (N₂) ее точек, расположенных на главном меридиане.

 

Пример 50

Построить проекции линии пересечения плоскости Р с поверхностью конуса. (рис. 71).

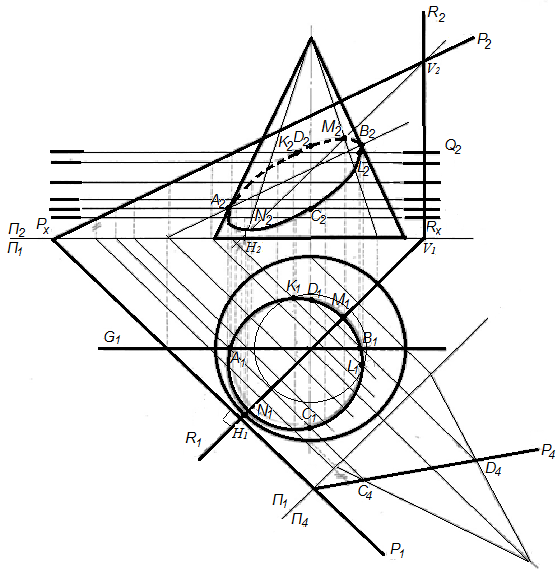
Рисунок 71

Решение. Проводим через ось конуса горизонтально-проецирующую плоскость R, перпендикулярную к плоскости Р. Плоскость R пересекает поверхность конуса по образующим, а плоскость Р — по прямой (H₁V₁, H₂V₂); на их пересечении получаем низшую точку (N₁, N₂) и высшую точку (M₁, M₂) линии пересечения. Проводим через ось конуса плоскость G параллельную плоскости V; плоскость G пересекает поверхность конуса по крайним образующим, а плоскость Р — по фронтали; на их пересечении получаем еще две точки (А₁, А₂)и(В₁, В₂) линии пересечения.

Для того чтобы найти точки линии пересечения, лежащие на профильных образующих, заменяем фронтальную плоскость проекций новой (П₄), где плоскость Р — фронтально-проецирующая, и находим точки (С₁, С₄) и (D₁, D₄) пересечения этих образующих с плоскостью P. Затем находим точки (С₁, С₂) и (D₁, D₂).

Для того чтобы найти промежуточные точки линии пересечения, поступаем так: вводим между точками (N₁, N₂) и (M₁, M₂) вспомогательную плоскость Q, параллель­ную плоскости П₁; плоскость Q пересекает поверхность конуса по окружности, а плоскость Р — погоризонтали; на их пересечении получаем две точки (K₁, K₂) и (L₁, L₂). Аналогично находим еще несколько точек и затем через одноименные проекции найденных точек проводим плавные кривые — эллипсы.

 

Пример 51

Построить проекции линии пересечения плоскости Рс поверхностью шара.

Решение. Проводим через центр шара горизонтально-проецирующую плоскость R, перпендикулярную к плоскости Р; плоскость R пересекает поверхность шара по окружности, а плоскость Р — по прямой (H₁V₁, H₂V₂); на их пересечении получаем низшую точку (N₁,N₂) и высшую точку (M₁, M₂) линии пересечения (рис. 72). Для того чтобы не строить эллипса на фронтальной плоскости проекций, совмещаем плоскость R с горизонтальной плоскостью проекций и находим предварительно эти точки в совмещенном положении (см. рис. 72).

Рисунок 72

Для того чтобы найти промежуточные точки линии пересечения, проводим между точками (N₁,N₂) и (M₁, M₂) ряд вспомогательных плоскостей, параллельных горизонтальной плоскости проекций. Например, плоскость Q пере­секает поверхность шара по окружности, а плоскость Р — по горизонтали; на их пересечении получаем две точки: (1₁, 1₂) и (2₁, 2₂).

Для того чтобы на фронтальной проекции кривой отделить видимую ее часть от невидимой, проводим через центр шара плоскость G (G₁) параллельную фронтальной плоскости проекций; плоскость G пересекает поверхность шара по главному меридиану, а плоскость Р — по фронтали. На их пересечении получаем точки (A₁, A₂) и (B₁,B₂). Для того чтобы на горизонтальной проекции кривой отделить видимую ее часть от невидимой, проводим через центр шара плоскость, параллельную горизонтальной плоскости проекций; плоскость S пересекает поверхность шара по экватору, а плоскость Р — по горизонтали. На их пересечении получаем точки (3₁, 3₂) и (4₁, 4₂). Затем одноименные проекции всех найденных точек соединяем плавными кривыми — эллипсами.

 

Пример 52

Построить линии пересечения конуса тремя плоскостями P, G, T"', образующими сквозное отверстие.

Рисунок 73

Решение: 1) Плоскости T', T" и T"' являются горизонтальными плоскостями уровня (параллельные П₁), при пересечении с конусом они образуют линии, которые на горизонтальную плоскость проецируются в виде окружности (рис. 73). Вначале строятся фронтальные проекции точек, которые так же лежат на фронтально-проецирующей плоскости G. Далее они проецируются на горизонтальную плоскость на соответствующие окружности на горизонтальной плоскости проекций..

2) Плоскость Р пересекает конус по образующей, которая на горизонтальной плоскости представлена в виде прямой, проходящей через вершину конуса.

3) Соединив полученные точки, получаем линию, образующую сквозное отверстие.

 

Рисунок 74

Пример 53

Построить линии пересечения сферы с плоскостью общего положения S, заданную двумя пересекающимися прямыми l и m (рис. 74).

Решение: Окружность сечения проецируется на плоскости проекций в эллипсы. Задача решена (рис. 74) путем замены системы плоскостей П2/П1 системой П4/П1, в которой плоскость является проецирующей (S₄).

 

Пример 54

Провести через прямую АВ плоскость, пересекающую поверхность наклонного цилиндра по образующим, и найти эти образующие (рис.75).

Рисунок 75

Решение. Задаем на прямой АВ произвольную точку K и проведем через нее прямую КL параллельную оси цилиндра. Прямые AB и KL определяют искомую плоскость. Находим горизонтальные следы (H₁, H₂) и (H'₁, H'₂) этих прямых и проводим через точки H₁ и H'₁ горизонтальный след (Р₁) плоскости; на его пересечении с основанием цилиндра получаем точки (N₁, N₁) и (M₁, M₂), через которые проводим искомые образующие.

Примечание. В частном случае (когда?) горизонтальный след (Р₁) плоскости может касаться основания цилиндра, тогда эта плоскость является касательной к поверхности цилиндра.

 

Рисунок 76

Пример 55

Найти линию пересечения цилиндра с конусом с помощью сфер (рис. 76).

Решение. Принимаем точку (С₁, С₂) пересечения осей цилиндра и конуса за центр вспомогательных шаровых поверхностей. Описываем из точки (С₁, С₂) шар произвольного радиуса R, который (шар) пересекает каждую из данных поверхностей по окружности; вертикальные их проекции—прямые линии, а горизонтальные проекции- эллипсы (последние для решения задачи не нужны и потому их не строим). На пересечении этих прямых линий получаем вертикальные проекции (1₂) и (2₂) точек; по ним, пользуясь вспомогательными образующими (или окружностями), находим горизонтальные проекции (7) и (2) точек. Аналогично, изменяя только радиус шара, получаем еще ряд точек. Соединив эти точки кривой линией, находим искомую линию пересечения.

 

Пример 56

Дать развертку боковой поверхности прямого кругового цилиндра (рис. 77).

Решение. Разверткой боковой поверхности прямого кругового цилиндра, радиус основания которого равен r, а высота l), является прямоугольник с основанием длиной 2pr и высотой l. Для того чтобы избежать вычислений, связанных с определением длины окружности, обычно вписывают в основание цилиндра правильный 12-угольник (на чертеже показываем только вершины 0, 1, 2 и т. д.), и его периметр принимают за длину основания прямоугольника. Таким образом развертку боковой поверхности прямого кругового цилиндра заменяют с достаточной для практики точностью разверткой боковой поверхности прямой правильной 12-угольной призмы, вписанной в данный цилиндр.

 

Рисунок 77

Показываем дополнительно, как перенести точку (K₁,K₂) с поверхности цилиндра на его развертку. Откладываем на основании прямоугольника отрезок ОМ, равный длине выпрямленной дуги OM₁, и, восставив в точке М перпендикуляр, откладываем на нем отрезок МК, равный M₂K₂.

 

Пример 57

Дать развертку боковой поверхности наклонного конуса с круговым основанием (рис. 78).

Решение. Делим основание конуса на 12 равных частей и проводим через точки деления образующие. Таким образом, всю боковую поверхность конуса разбиваем на 12 криволинейных треугольников, которые с достаточной для практики точностью можно заменить плоскими треугольниками; следовательно, боковая поверхность конуса заменяется боковой поверхностью двенадцатиугольной пирамиды, вписанной в этот конус.

 

<

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: